Dawid Trzcionka
91610
WPROWADZENIE DO SYSTEMÓW TELEKOMUNIKACYJNYCH
-SEMINARIUM-
SEM. ZIMOWY 2000/2001
Prowadzący
Dr inż. Wojciech J. Krzysztofik
ZADANIE 4/2
Sygnał losowy o gęstości prawdopodobieństwa opisanej funkcją Gaussa:
![]()
-* < x < *
jest poddany kompresji z charakterystyką typu A (A=87,6). Dla jakiej wartości odchylenia standardowego σ stosunek mocy sygnału do mocy szumów kwantyzacji (P/E2) przy idealnym kwantowaniu logarytmicznym będzie taki sam jak przy kwantowaniu równomiernym?
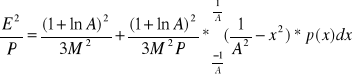
(1)
gdzie:
![]()
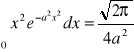
Wstęp teoretyczny.
Charakterystyka kompresji logarytmicznej typu A ma postać:
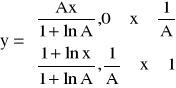
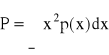
moc sygnału
Moc szumów kwantyzacji w przypadku kwantowania równomiernego wynosi:
![]()

Dla kwantowania równomiernego stosunek mocy szumów kwantyzacji do mocy sygnału:
Stosunek mocy szumów kwantyzacji do mocy sygnału dla sygnału poddanego kompresji z charakterystyką A wynosi:
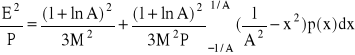
Pierwsza część po prawej stronie wyrażenia przedstawia stosunek szum/sygnał przy idealnym logarytmicznym kwantowaniu. Druga część odpowiada wzrostowi szumu spowodowanego nieidealnym kwantowaniem.
Rozwiązanie zadania
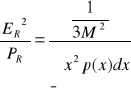
Kwantowanie równomierne
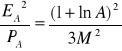
Kwantowanie idealne
Aby rozwiązać zadanie należy porównać ze sobą wyrażenia na stosunek moc szumu/moc sygnału przy kwantowaniu równomiernym i kwantowaniu idealnym logarytmicznym.
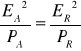
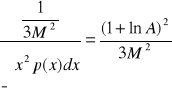
Moc P sygnału p(x) wyraża się wzorem
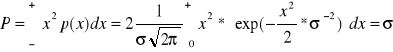
.
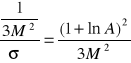
![]()
A=87,6
σ=0,033
![]()
Odp. Dla odchylenia standardowego σ=0,033, stosunek mocy sygnału do mocy szumów kwantyzacji przy idealnym kwantowaniu logarytmicznym będzie taki sam jak przy kwantowaniu równomiernym.
3
Wyszukiwarka
Podobne podstrony:
z4 06, SPRAWOZDANIA czyjeś
z1 02, SPRAWOZDANIA czyjeś
Z4 03, SPRAWOZDANIA czyjeś
z2 02, SPRAWOZDANIA czyjeś
z4 05pg, SPRAWOZDANIA czyjeś
Z4-01, SPRAWOZDANIA czyjeś
więcej podobnych podstron