Definicje i kryteria stabilności

Niech 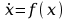będzie równaniem stanu autonomicznego układu nieliniowego.

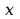jest n w ymiarowym wektorem stanu

jest n wymiarową funkcją nieliniową.

W przypadku układu liniowego stacjonarnego równanie to przyjmuje postać :

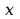jest n w ymiarowym wektorem stanu

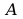jest macierzą o wymiarach 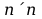i stałych niezależnych od czasu elementach.

Def. Punktem równowagi układu 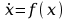nazywamy punkt 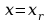,dla którego .

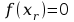(Jeżeli punkt równowagi nie pokrywa się z początkiem układu współrzędnych 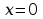,to przez odpowiednią zamianę współrzędnych można sprowadzić go do tego punktu .)

Załóżmy , że układ został wytrącony ze stanu równowagi i w chwili początkowej znajduje się w stanie .

Def. Punkt równowagi 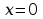nazywamy stabilnym ( w sensie Lapunowa ) jeżeli dla każdej liczby dodatniej można dobrać taką liczbę ( zależną na ogół od ) , że trajektoria rozpoczynająca się w punkcie , leżącym wewnątrz kuli o promieniu , pozostanie wewnątrz kuli o promieniu dla dowolnej chwili .

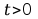Def. Punkt równowagi 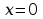nazywamy stabilnym asymptotycznie , gdy

1⁰ punkt ten jest stabilny

2⁰ .

Def. Układ liniowy stacjonarny nazywamy stabilnym (stabilnym asymptotycznie ) ,jeżeli punkt równowagi 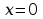tego układu jest stabilny ( stabilny asymptotycznie ) .

Układ liniowy stacjonarny jest globalnie stabilny asymptotycznie , gdzie wartości własne macierzy 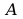, tzn. takie że .

Obliczając wyznacznik mamy wielomian charakterystyczny .

Zatem dla stabilności asymptotycznej badamy położenie pierwiastków względem osi urojonej .

Wartości własne macierzy 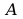o ujemnych częściach rzeczywistych leżą w lewej półpłaszczyżnie płaszczyzny zmiennej zespolonej .

Kryterium Hurwitza

Wielomian ma wszystkie pierwiastki w lewej części płaszczyzny zespolonej gdy wszystkie główne diagonalne minory

, , ,... ,

,

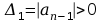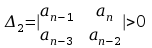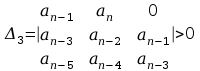tzn. aby dodatnie były minory diagonalne jego macierzy Hurwitza .

Neutralnie stabilny system automatycznego sterowania to taki system, w którym po ustaniu wymuszenia ustala się nowy stan równowagi, różny od początkowego i zależny od działającego wymuszenia.

Niech system opisany : a­­₀x⁽ⁿ⁾ + a₁x^(n-1) +...+ a_nx⁽¹⁾ = 0 ma jeden zerowy pierwiastek. Jest to możliwe, gdy : a_n = 0. Wówczas równanie charakterystyczne ma postać :

(a₀λ^n-1 + a₁λ^n-2 +...+ a_n-1)λ = 0

oznaczamy prędkość zmiennej x przez V = x’. Wówczas mamy

a₀V^n-1 + a₁V^n-2 +...+ a_n-1V = 0

a więc system okazuje się asymptotycznie stabilny względem V. Sama funkcja x(t) może przyjmować dowolne wartości. Dlatego takie systemy nazywamy stabilnymi neutralnie.