1. Zestaw

Ruch po okręgu. Gdy ciało porusza się po okręgu wektor jego prędkości, stycznego toru, będzie stale zmieniał swój kierunek. Oznacza to, że wektor prędkości nie jest stały a zatem ruch po okręgu jest ruchem zmiennym. Jeżeli jednak wektor prędkości zmieniając swój kierunek zachowa przy tym stałą wartość to taki ruch będzie ruchem jednostajnym po okręgu. Ruch jednostajny po okręgu jest ruchem okresowym tzn. ruchem, który powtarza się w regularnych odstępach czasu. Okres, który definiujemy jako czas trwania jednego pełnego obiegu jest przy tym równy T=2Πr/v r- promień okręgu v - prędkość ciała poruszającego się po okręgu. Liczbę pełnych obiegów wykonanych w jednostce czasu nazywamy częstotliwością ruch po okręgu. Częstotliwość f i okres T są ze sobą związane zależnością T=1/f [sek=l/Hz]. Przyspieszenie w ruchu jednostajnym po okręgu jest skierowane wzdłuż promienia okręgu i zwrócone do środka okręgu dlatego właśnie przyspieszenie w tym ruchu nazywamy przyspieszeniem dośrodkowym lub normalnym |a_n|-|v|/|r|+lim|Δr|/|Δt|+v²/r Przyspieszenie ciała w ruchu jednostajnie zmiennym po okręgu można rozłożyć na dwie składowe: normalną - odpowiedzialna za zmianę kierunku prędkości ciała i styczną - odpowiedzialną za zmianę wartości prędkości ciała a=lim[(ΔV₁+ ΔV₂)/Δr.

Moment pędu L punktu materialnego o masie m. i wektorze wodzącym r, poruszającego się z prędkością v względem osi obrotu odległej o r od tego punktu, definiujemy wzorem L=rxvm. Wektor momentu pędu jest skierowany zgodnie z osią obrotu. Jego wartość bezwzględna, wynosi L=rmv=mr²ω. Moment pędu bryły jest sumą momentów pędów wszystkich jej punktów, czyli L=Σm₁r₁²=ωΣm₁r₁²=Iω Moment pędu bryły równa się iloczynowi jej prędkości kątowej i momentu bezwładności. Pochodna momentu pędu bryły względem czasu jest równe momentowi siły działającej na tę bryłę M.=aI=Idω/dt=d(Iω)/dt=dL/dt.Fala harmoniczna: Najprostsza fala to tzw. fala harmoniczna płaska. Drgania dla takiej fali są sinusoidalną funkcją czasu - inaczej mówiąc: każdy punkt ośrodka wykonuje drgania harmoniczne (sinusoidalne). Dla takiej fali można dobrze określić dwa ważne parametry: 1:okres fali T, lub częstotliwość fali f2:długość fali  λ Długość fal:Długość fali widoczna jest najlepiej wtedy, gdy na chwilę "zatrzymamy" falę w jej ruchu - sfotografujemy ją.Wtedy długością będzie najmniejsza odległość między dwoma punktami fali, różniącymi się o dokładnie jeden cykl tych drgań - np. pomiędzy dwoma najbliższymi szczytami fali, ew. "dołami" fali. Może to być też odległość między punktami, które akurat nie ulegają w danej chwili wychyleniu. Okres fali jest wielkością, którą najlepiej widać, gdy skupimy się na drganiu jednego konkretnego punktu ośrodka. Na rysunku niżej czerwony koralik jest pobudzany przez falę do drgań  góra - dół. Okres tych drgań wynosi 1,5 s, co oznacza, że czas, po jakim koralik wykona jedno pełne drganie wynosi właśnie 1,5 s.

2. Zestaw

 Środek masy. Pojęcie środka masy jest bardzo użyteczne, gdyż jak się przekonamy, pozwala na znakomite uproszczenie opisu ruchu układu składającego się z wielu ciał. Zamiast rozpatrywać poszczególne ruchy dużej ilości ciał, wystarczy w wielu przypadkach rozważyć jedynie ruch jednego punktu będącego środkiem mas układu tych ciał. Rozważmy dwa ciała o masach m₁ i m₂ położone na osi X w punktach x₁ i x₂ odległe od siebie o l = x₂ - x₁ (patrz rysunek). Punkt S, który dzieli odcinek l w stosunku odwrotnie proporcjonalnym do mas tych ciał nazywamy środkiem masy układu dwóch ciał (punktów materialnych). Środek masy może być w spoczynku lub poruszać się podczas ruchu poszczególnych ciał układu. Zapytajmy, jaka jest prędkość środka masy v_S, gdy znane są prędkości i masy ciał układu. Pisząc dwa powyższe równania dla dwóch różnych chwil czasu i odejmując je od siebie stronami, otrzymamy: W przypadku, gdy układ jest odosobniony, jego całkowity pęd jest stały i wtedy prędkość środka masy jest również stała co do wartości i co do kierunku, czyli środek masy porusza się ruchem bezwładnym, niezależnie od tego, jak poruszają się części składowe układu. Na układ odosobniony nie działają siły zewnętrzne. Widzimy zatem, że siły wewnętrzne nie wpływają na ruch środka masy.
Jak zachowuje się środek masy, gdy na układ działają siły zewnętrzne? Środek masy uzyskuje wtedy przyspieszenie a_S, które można obliczyć z drugiej zasady dynamiki Newtona:

Drgania harmoniczne (swobodne). Rozważamy drgania, jakie wykonuje punkt materialny o masie m. pod działaniem siły sprężystości F_s=-kx. Zgodnie z II zasadą dynamiki F_s= ma, zatem -kx=m(d²x/dt²) czyli m(d²x/dt²)+kx=0 , jest to równanie różniczkowe drgań swobodnych punktu materialnego. Łatwo można sprawdzić, że jeśli zachodzi zależność ω=√k/m . Drgania swobodne są zatem drganiami harmonicznymi. Częstotliwość drgań swobodnych ciał nazywamy częstotliwością własną. Drgania swobodne możemy obserwować zawieszając na sprężynie ciężarek i wytrącając go z równowagi. Drgania swobodne wykonuje też wahadło matematyczne. Drgania swobodne nie muszą być wyłącznie mechaniczne: np. w obwodzie elektrycznym złożonym z indukcyjności i pojemności występują drgania swobodne elektryczne. Energia całkowita drgającego harmonicznie punktu materialnego. Jego E_k= 1/2mv²=1/2mAsin²(ωt+φ), a E_ρ=1/2kx²=1/2kA²cos² (ωt+φ). Całkowita energii mechaniczna E=E_ρ+E_k=1/2A²[mω²sin²(ωt+φ)+kcos²(ωt+φ)] =1/2kA². Wdać, że w ruchu harmonicznym E_k i E_ρ punktu wykonującego drganie zmieniają się w taki sposób, że ich suma pozostaje stała.

Prawo 0hma. W przewodnikach metalicznych natężenie prądu jest dla danego przewodnika wprost proporcjonalne do przyłożonego napięcia I=G*U. Współczynnik proporcjonalności G nazywa się przewodnością i mierzy się go w [simensach]. Podane prawo Ohma można podać innej postaci I=U/R gdzie R nazywa się opornością danego przewodnika i mierzy się w [Omach Ω] Prawo Ohma stosuje się tylko do przewodników liniowych.

Siły van der Waalsa. Własności gazów rzeczywistych najlepiej opisuje van der Waalsa, w który zawarte są dwie poprawki: 1) objętość własna cząsteczek gazu; objętość swobodna gazu jest zatem mniejsza od objętości naczynia o objętość własną, którą oznaczamy literą b (dla jednego mola gazu); 2) siły międzycząsteczkowe; wskutek wzajemnego przyciągania się cząsteczek gazu, ciśnienie całkowite jest sumą ciśnienia zewnętrznego i wewnętrznego, która wynosi a/V² (p + a/Vo²)(V_o-b)=RT; a i b stałe charakterystyczne dla danego gazu pV₀³-(pb+RT)V₀²+aV₀-ab=0,V_o³-(b+RT/p)V₀²+aVo/p-ab/p=0. Uwzględniając równanie trzeciego stopnia to: (V_o-V_okr)³=0, czyli V_o³-3V_o² V_okr+3 V_o V²_okr- V³_okr=0, wynikają związki P/P_k-Pzr , Vo/V_k-Vzr , T/T_kc-Tzr , czyli (Pzr+3/V²ozr)(Vozr-1/3)-8/3*Tzr

3. zestaw

Zasady dynamiki Jeżeli na ciało nie działa żadna siła bądź działające wypadkowe sił się równoważą to ciało to pozostaje w spoczynku bądź porusza się ruchem jednostajnym prostoliniowym Jest to zasada powszechnie znana jako zasada bezwładność ciała. Np. Pasażerowie jadący tramwajem przewracają się przy nagłym zahamowaniu pojazdu, gdyż wskutek swej bezwładności nadal poruszają się do przodu z poprzednią prędkością, mimo tego, że tramwaj już swoją prędkość zmienił. Pierwsza zasada dynamiki leży u podstaw statyki punktu materialnego. Określa ona bowiem warunki, przy spełnieniu których punkty materialne spoczywają. Jeżeli punkt materialny ma spoczywać to wg. I zasady dynamiki nie mogą na niego działać żadne siły zewnętrzne lub gdy siły takie działają to ich wypadkowa musi być równa zeru. Oznacza to że warunek konieczny jaki musi być spełniony bt punkt materialny spoczywał można zapisać w postaci ΣFi=F1+F2+F3+...+Fn=0 W II zasadzie dynamiki podaje się zwykle dwa sformułowania tej zasady. Wg pierwszego: ciało, na które działa siła niezrównoważona, porusza się ruchem przyspieszonym z przyspieszeniem proporcjonalnym do wartości tej siły, skierowanym i zwróconym tak samo jak działająca na dato siła. Im większa jest masa data tym większą siła trzeba działać na to ciało by nadać mu to samo przyspieszenie. Drugą zasadę dynamiki w jej pierwszym sformułowaniu można wyrazić następującą zależnością F=ma. W drugim sformułowaniu które jest poprawne również wtedy gdy ruch ciała będzie się odbywał z bardzo wielką prędkością przy której wystąpi zmiana masy opisana wzorem m=m0/√1-(v²/c²)Wymaga to jednak zdefiniowania dwóch nowych wielkości dynamicznych: pędu ciała i popędu siły .Pędem ciała nazywamy wielkość wektorową równą iloczynowi masy data i jego prędkości p=mv. Popędem siły nazywamy iloczyn siły i czasu, w ciągu którego ta siła działa na ciało. Druga zasada dynamiki w swoim sformułowaniu brzmi: Przyrost pędu ciała jest równy popędowi siły działającej na to ciało Π=F Δt .III zasada dynamiki brzmi następująco; Jeżeli ciało A działa na ciało B z pewną siłą to ciało B działa na ciało A z siłą równą co do wartości i kierunku ale przeciwnym zwrocie wektorowo F_ab=-F_ba, skalarnie F_ab=F_ba. Siły wynikające z III zasady dynamiki są przyłożone do różnych ciał, a zatem błędem byłoby twierdzić, że się równoważą. Równoważyć się tylko mogą siły przyłożone do jednego ciała. III zasada informuje nas o tym ze każdemu działaniu towarzyszy przeciwdziałanie Np. jeżeli naciskamy palcem na stół to czujemy ze stół także oddziałuje na nasz palec i to tym silniej im silniej naciskamy.

Dudnienie. Przy nałożeniu się drgań harmonicznych o niewiele różniących się pulsacjach powstaje drganie złożone, które nazywamy dudnieniem. Załóżmy, że drgania składowe mają jednakowe amplitudy x₁=Acosω₁t=Acos(ω+∆v)t; x₂=Acos(ω+∆v)t, gdzie ω =ω₁+ ω₂/2 , ∆v=ω₂+ ω₁/2. Drganie wypadkowe wyraża się wzorem x=Acos(ω+∆v)t+Acos(ω-∆v)t=2Acos∆v cosωt=Acosωt Amplituda ta zmienia się periodycznie w czasie. Dudnienie można usłyszeć gdy, np. w Instrumentach muzycznych dwie struny są nastrojone na niewiele różniące się tony: kiedy obie struny wydają dźwięk, słyszymy dudnienie.

Pierwsza zasada termodynamikiTo jest po prostu inna wersja zasady zachowania energii, w której mamy rozdzieloną energię ciała na część makroskopową i mikroskopową. Makroskopowa to energia ruchu masy (energia mechaniczna). Mikroskopowa to "ukryta" energia cząstek (energia wewnętrzna).Gdy dwa układy (ciała) o różnych temperaturach zetkniemy ze sobą to ciepło ΔQ przepływa z ciała cieplejszego do chłodniejszego. Zgodnie z zasadą zachowania energii, ciepło pobrane przez układ musi być równe wzrostowi energii wewnętrznej układu plus pracy wykonanej przez układ nad otoczeniem zewnętrznym czyli ΔQ = ΔU + ΔW To jest sformułowanie I zasady termodynamiki.

Zasada ta pracuje "w obie strony" tzn., gdy nad układem zostanie wykonana praca to układ może oddawać ciepło. To równanie bardzo często przybiera postać

4. zestaw

Zderzeniach niesprężystych energia kinetyczna nie jest zachowana.Różnica pomiędzy energią kinetyczną początkową i końcową przechodzi np. w ciepło lub energię potencjalną deformacji.Przykład 1część swej energii kinetycznej traci neutron (m₁) w zderzeniu centralnym z jądrem atomowym (m₂) będącym w spoczynku?Początkowa energia kinetyczna:
Końcowa energia kinetyczna:
Względne zmniejszenie energii inetycznej: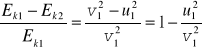

Natężenie prądu (nazywane potocznie prądem elektrycznym) jest stosunkiem ilości ładunku elektrycznego przepływającego przez przekrój poprzeczny przewodnika do czasu przepływu ładunku. Sama bateria, czy też prądnica nie mają natężenia. Natężenie jest zależne od poboru prądu.I=dq/dt Jednostką natężenia prądu w Układzie SI jest amper [A].Natężenie prądu stałego oznaczamy literą I, a prądu zmiennego przez i(t), aby podkreślić zmiany w czasie.Do pomiaru natężenia prądu elektrycznego służy amperomierz. Urządzeniem do definicyjnego yznaczania jednostki jest waga prądowa, wyparta przez o wiele dokładniejsze kalibratory prądu.Natężenie prądu można zmniejszać stosując rezystory. Rezystor dobieramy przy pomocy prawa Ohma:R=U/I R - opór (Ω) U - napięcie (V) I - natężenie (I)Zwarty obwód bez rezystora ma bardzo duże, choć ograniczone znikomą rezystancją przewodników natężenie.- intuicyjnie jest to wielkość fizyczna określająca natężenie prądu elektrycznego przypadającego na jednostkę powierzchni przewodnika. Wyrażana jest w A/m². W praktyce stosuje się na ogół wygodniejsze jednostki: A/cm² i A/mm²ęstość prądu definiujemy jako:J=I/S, gdzie:I - natężenie prądu płynącego przez przewodnik,S - Pole przekroju poprzecznego przewodnika.Formalnie gęstość prądu jest wektorem zdefiniowanym za pomocą wzoru:
gdzie:J - wektor gęstości prądu(sigma)- tensor przewodnictwa elektrycznego E- wektor natężenia pola elektrycznego Oczywiście dla dowolnej powierzchni zamkniętej S zachodzi:
dzieQ - ładunek zgromadzony w obszarze ograniczonym powierzchnią S. ds- wektor skierowany na zewnątrz powierzchni SPowyższe równanie nosi nazwę zasady zachowania ładunku. Można je sprowadzić do częściej spotykanej postaci różniczkowej (zwanej równaniem ciągłości) przez podzielenie go przez objętość ograniczoną przez powierzchnię S i przejście do granicy z V )Otrzymujemy w tedy:
gdzieρ - gęstość objętościowa ładunku

Fala stojąca. Fala wytworzona w ciele o skończonych rozmiarach odbija się od granic tego ciała. Fala odbita porusza się w przeciwnym kierunku co fala padająca i superpozycja tych dwóch fal daje w wyniku fale wypadkową zwaną falą stojącą. Załóżmy, że mamy do czynienia z falą harmoniczną i że fala odbita ma tę samą amplitudę co fala padająca ξ₁=Asin(kx-ωt), ξ₂=Asin(kx+ωt, stąd fala wypadkowa ξ=ξ₁+ξ₂=2Asinkxcosωt, jest to równanie fali stojącej. Amplituda drgań przybiera wartość max. 2A w punktach, w których kx=π/2,3π/2,5π/2.., a wartość minimalną, równą zero w punktach kx=0,π,2π,3π,... Maksymalną amplitudę drgań nazywamy strzałkami, ponieważ zachodzi zależność k=2π/λ, strzałki znajdują się w punktach x=λ/4,3λ/4,5λ/4,.. a punkty, w których amplituda drgań jest równa zero, nazywane są węzłami x=0λ/2,3λ/2,... Węzły i strzałki położone są na przemian, a odległości między węzłami lub kolejnymi strzałkami wynosi pół długości fali.

Rzut ukośny. Ciało wyrzucone z prędkością początkową V₀ tworzą kąt φ z poziomem. Jeżeli układ współrzędnych obierzemy tak, aby oś y była skierowana pionowo w górę i aby w chwili początkowej ciało znajdowało się w początku układu, to przyspieszenie ciała w czasie rzutu będzie równe przyspieszeniu ziemskiemu i będzie skierowane pionowo w dół. Współrzędne prędkości ciała wynoszą V_0x=v₀cosφ, V_0y=v₀sinφ W kierunku poziomym ruch jest jednostajny, ponieważ a,=0, więc x=V_0xt=V₀tcosφ. W kierunku poziomym ruch jest jednostajnie opóźniony z przyspieszeniem a_y=-g, więc y=V_0yt+a_yt/2=V₀tsin φ-gt²/2. Z dwóch ostatnich równań otrzymujemy równanie toru y=xtgφ-x²g/2v²₀cos2φ. Ze wzoru na równanie toru otrzymujemy wzór na zasięg rzutu D=v₀²sin2φ/g. Wysokość rzutu znajdujemy podstawiając do wzoru wartość x=D/2, h=V₀² sin²φ/2g.

5. zestaw

Równanie Van der Waalsa Równanie stanu gazu doskonałegopV = nRTdobrze opisuje gazy rzeczywiste ale przy małych gęstościach. Przy większych gęstościach nie można pominąć faktu, że cząstki zajmują część objętości dostępnej dla gazu oraz że zasięg sił międzycząsteczkowych może być większy niż odległości międzycząsteczkowe.J.D. Van der Waals wprowadził zmienione równanie stanu gazu, które uwzględnia te czynniki. Jeżeli cząstki posiadają skończoną objętość to rzeczywista objętość dostępna dla cząstek jest mniejsza od objętości naczynia. "Objętość swobodna" jest mniejsza od objętości naczynia o "objętość własną" cząsteczek b. Jeżeli oznaczymy przez v objętość przypadającą na jeden mol v = V/n to otrzymamy zmodyfikowane równanie stanu gazu.p(v - b) = RTMożna również prosto uwzględnić efekt sił międzycząsteczkowych. Siły przyciągania pomiędzy n cząsteczkami (na jednostkę objętości) "po lewej" z n cząsteczkami (na jednostkę objętości) "po prawej" jest proporcjonalna do n² czyli proporcjonalna do 1/v². Siła przyciągająca znajduje swoje odzwierciedlenie w dodatkowym ciśnieniu, które zostało uwzględnione w równaniu Van der Waalsa
gdzie stałe a i b wyznaczamy doświadczalnie. (Równanie Van der Waalsa też bywa zawodne ale nie jest znana prosta formuła, która stosowałaby się do różnych gazów w różnych warunkach).

Na rysunku poniżej porównano zachowanie się gazu doskonałego (rysunek po lewej) w stałej temperaturze z gazem Van der Waalsa (po prawej).

Moment pędu L punktu materialnego o masie m. i wektorze wodzącym r, poruszającego się z prędkością v względem osi obrotu odległej o r od tego punktu, definiujemy wzorem L=rxvm. Wektor momentu pędu jest skierowany zgodnie z osią obrotu. Jego wartość bezwzględna, wynosi L=rmv=mr²ω. Moment pędu bryły jest sumą momentów pędów wszystkich jej punktów, czyli L=Σm_ir_i²ω=ωΣm_ir²_i=Iω. Moment pędu bryły równa się iloczynowi jej prędkości kątowej, i momentu bezwładności. Pochodna momentu pędu bryły względem czasu jest równe momentowi siły działającej na tę bryłę M.=αI=Idω/dt=d(Iω)/dt=dL/dt.

Zasada zachowania momentu pędu. Moment pędu bryły L=Iω, przy czym zgodnie z II zasadą dynamiki ruchu obrotowego pochodna krętu jest równa momentowi siły M.-dL/dt. Rozważając układ złożony z n ciał, które mogą być traktowane jak bryły sztywne. Dla dowolnej bryły obowiązuje równanie M.i=dL_i/dt. Sumując stronami dla wszystkich brył otrzymujemy ΣM._i=ΣdL_i/dt=d/dtΣL_i. Po lewej stronie mamy sumę momentów wszystkich sił działających na układ. Po lewej stronie otrzymaliśmy sumę krętów. Sumę krętów ciał należących do danego układu nazywamy krętem całkowitym albo krętem wypadkowym. Oznaczając całkowity kręt przez L, otrzymujemy M._z=dL/dt. Pochodna krętu całkowitego układu względem czasu jest równa momentowi wypadkowemu sił zewnętrznych. W przypadku, gdy siły zewnętrzne nie działają lub ich moment wypadkowy równa się zero M._z=0, to L=const. Jeśli moment wypadkowy sił zewnętrznych działający na układ równa się zero, to całkowity kręt tego układu jest stały.

Moment pędu L punktu materialnego o masie m. i wektorze wodzącym r, poruszającego się z prędkością v względem osi obrotu odległej o r od tego punktu, definiujemy wzorem L=rxvm. Wektor momentu pędu jest skierowany zgodnie z osią obrotu. Jego wartość bezwzględna, wynosi L=rmv=mr²ω. Moment pędu bryły jest sumą momentów pędów wszystkich jej punktów, czyli L=Σm₁r₁²=ωΣm₁r₁²=Iω Moment pędu bryły równa się iloczynowi jej prędkości kątowej i momentu bezwładności. Pochodna momentu pędu bryły względem czasu jest równe momentowi siły działającej na tę bryłę M.=aI=Idω/dt=d(Iω)/dt=dL/dt. Zasada zachowania pędu. Wg II zasady dynamiki dla dowolnego punktu zachodzi zależność: F_i=m_ią_i=dp_i/dt. Pisząc równanie dla wszystkich punktów i sumując je stronami, otrzymujemy ΣF_i=Σdp_i/dt=d/dtΣp_i. Sumę pędów wszystkich ciał należący do układu fizycznego nazywamy pędem całkowitym układu; pęd całkowity, zwany też-pędem wypadkowym, oznaczamy przez p F_z=dp/dt Pochodna pędu całkowitego układu względem czasu jest równa wypadkowej sił zewnętrznych działających na układ. Szczególnym przypadkiem układu punktów jest układ, na który siły zewnętrzne nie działają lub ich wypadkowa Jest równa zeru, gdy F_z=0, to p=const. Jeżeli wypadkowa sit zewnętrznych działających na układ jest równa zero, to całkowity pęd tego układu jest stały.

Pędem cała nazywamy iloczyn mas i jego prędkości p=mv. Z definicji tej wynika, że pęd jest wektorem skierowanym zgodnie z wektorem prędkości.

Indukcja własna i wzajemna. Jeśli w jednym obwodzie zmienia się natężenie prądu, to zgodnie z prawem indukcji Faradaya w drugim obwodzie znajdującym się w pobliżu pierwszego indukowana jest SEM. Zjawisko to zwane jest indukcją wzajemną i oznaczone przez Φ₂₁.e_ind2.=dΦ₂₁/dt. Strumień Φ₂₁ jest proporcjonalny do I₁. Oznaczając współczynnik proporcjonalności przez L₂₁ można napisać Φ₂₁=L₂₁I₁. Zamieniając role obwodów Φ₁₂=L₁₂I₂. Współczynniki L₂₁ i L₁₂ zwane są współczynnikami indukcji wzajemnej. Można udowodnić, że jeśli w pobliżu nie ma materiałów ferromagnetycznych to współczynniki indukcji wzajemnej są równe i zależą tylko od kształtu i wzajemnego położenia obwodów e_ind2=L₂₁dI/dt. Z zależności tej wynika, że SEM indukowana w obwodzie 2 jest proporcjonalna do szybkości zmian natężenia prądu w obwodzie 1. W przypadku pojedynczego obwodu występuje tzw. zjawisko indukcji własnej. Strumień magnetyczny wytworzony przez prąd płynący w obwodzie przenika ten obwód, zatem każda zmiana natężenia prądu wywoła w nim SEM indukcji. Strumień magnetyczny Φ wytwarzany przez obwód i przenikający go jest proporcjonalny do natężenia prądu I płynącego w tym obwodzie Φ=LI. Współczynnik indukcji własne oznaczamy przez L, zatem e_ind2=-dΦ/dt=-LdI/dt. SEM samoindukcji odgrywa dużą rolę w obwodach układu zamkniętego. Ponieważ SEM przeciwdziała zmianom prądu, wiec gdy prąd rośnie, SEM działa przeciwnie do kierunku prądu, a kiedy prąd maleje to SEM działa w tym samym kierunku co prąd. W rezultacie obwód wykazuje większy opór dla prądu zmiennego niż dla prądu stałego.

Indukcja własna i wzajemna. Jeśli w jednym obwodzie zmienia się natężenie prądu, to zgodnie z prawem indukcji Faradaya w drugim obwodzie znajdującym się w pobliżu pierwszego indukowana jest SEM. Zjawisko to zwane jest indukcją wzajemną i oznaczone przez Φ₂₁.e_ind2.=dΦ₂₁/dt. Strumień Φ₂₁ jest proporcjonalny do I₁. Oznaczając współczynnik proporcjonalności przez L₂₁ można napisać Φ₂₁=L₂₁I₁. Zamieniając role obwodów Φ₁₂=L₁₂I₂. Współczynniki L₂₁ i L₁₂ zwane są współczynnikami indukcji wzajemnej. Można udowodnić, że jeśli w pobliżu nie ma materiałów ferromagnetycznych to współczynniki indukcji wzajemnej są równe i zależą tylko od kształtu i wzajemnego położenia obwodów e_ind2=L₂₁dI/dt. Z zależności tej wynika, że SEM indukowana w obwodzie 2 jest proporcjonalna do szybkości zmian natężenia prądu w obwodzie 1. W przypadku pojedynczego obwodu występuje tzw. zjawisko indukcji własnej. Strumień magnetyczny wytworzony przez prąd płynący w obwodzie przenika ten obwód, zatem każda zmiana natężenia prądu wywoła w nim SEM indukcji. Strumień magnetyczny Φ wytwarzany przez obwód i przenikający go jest proporcjonalny do natężenia prądu I płynącego w tym obwodzie Φ=LI. Współczynnik indukcji własne oznaczamy przez L, zatem e_ind2=-dΦ/dt=-LdI/dt. SEM samoindukcji odgrywa dużą rolę w obwodach układu zamkniętego. Ponieważ SEM przeciwdziała zmianom prądu, wiec gdy prąd rośnie, SEM działa przeciwnie do kierunku prądu, a kiedy prąd maleje to SEM działa w tym samym kierunku co prąd. W rezultacie obwód wykazuje większy opór dla prądu zmiennego niż dla prądu stałego.

6..Zestaw

Ruch falowy. Zaburzenia ośrodka materialnego przenoszące się z pewną prędkością z jednego punktu przestrzeni do innych punktów nazywamy falą mechaniczną. Fale mechaniczne dzieli się na fale poprzeczne i podłużne. Fala poprzeczna to taka fala, której ruch ośrodka następuje prostopadle do kierunku rozchodzenia się fal, fala podłużna jest to fala, której ruch ośrodka następuje równolegle do kierunku rozchodzenia się fal. Jest regułą, że fale mechaniczne poprzeczne mogą powstawać tylko w takich ośrodkach, które charakteryzują się sprężystością postaciową. Fale podłużne mogą natomiast powstawać w ośrodkach o sprężystości objętościowej lub postaciowej. Prędkość fal - prędkość, z jaką rozchodzi się w przestrzeni zaburzenie ośrodk. Dla fali poprzecznej v┴-√F/_m1F- siła przyłożona prostopadle do struny do jej długości, m1- masa przypadająca na jednostkę długości struny. Dla fali podłużnej - w ciałach stałychv║-√E/ξ E - moduł Younga, ξ - gęstość materiału, - w gazach v║ -√λp/ξ , λ - stałą dla danego gazu, p - ciśnienie gazu. W praktyce można spotkać się z ruchem falowym w postaci ciągu fal, w którym następujące po sobie regularne zaburzenia wytworzone w źródle są przekazywane przez ośrodek np. fala sinusoidalna ciągła w fali takiej wszystkie cząsteczki ośrodka drgają wokół swych położeń równowagi ruchem harmonicznym o tym samym czasie, lecz o różnej fazie początkowej. Równanie x=X₀simω(t-z/v) jest kinematycznym równaniem ruchu dla fali sinusoidalnej o jednej częstotliwości. Parametry fal: powierzchnia falowa jest to powierzchnia utworzona z punktów ośrodka znajdujących się w tej samej fazie drgania są to zwykle punkty jednakowo odległe od źródła fali. Czoło fali jest to powierzchnia fal, która jest najbardziej oddalona od źródła. Fala kulista jest to fala, której powierzchnie falowe są współśrodkowymi kulami, w których środku znajduje się źródło fali. Długość fali jest to odległość między dwoma powierzchniami falowymi różniącymi się fazą o 2Π-λ=v/f=2Πv/ω.

---