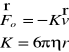Wstęp teoretyczny
Do płynów zaliczamy ciecze i gazy. Odróżniają się od ciał stałych tym, że przybierają kształt naczyń, w których są zamknięte, z tym że gazy zajmują całą objętość naczynia, natomiast ciecze tylko dolną część równą swojej objętości. Płyny dzielimy na ściśliwe i nieściśliwe (będące matematyczną idealizacją płynów rzeczywistych) oraz lepkie i nie-lepkie (He w warunkach nadciekłości: temp<2,1K oraz gazy idealne).
Lepkością nazywamy siłę oporów ruchu występującą w płynach.
|
Do ciała o powierzchni stycznej do powierzchni płynu przykładamy siłę F, skierowaną tak, jak na rysunku. Ciało powinno się poruszać, ze stałym przyspieszeniem a≠0. Ciało jednak porusza się z v=const, więc wnioskujemy, że musi na to ciało działać dodatkowa siła oporu, którą definiujemy jako:
Dodatkowo ruch ciała powoduje nadanie warstwom cieczy różnych prędkości, zależnych od odległości od ciała. |
η ([η]= kg/m·s) oznacza współczynnik, charakteryzujący płyn, zwany współczynnikiem lepkości.
Przepływ cieczy wokół dowolnego ciała zależy od kombinacji liniowej takich parametrów, jak gęstość cieczy ρ, współczynnik lepkości cieczy η, prędkość przepływu v i wymiar liniowy l. Wielkości te są związane w tzw. Liczbę Reynoldsa:
|
ρ- gęstość cieczy η- współczynnik lepkości cieczy v- prędkości przepływu l- wymiar liniowy |
Dla przepływu laminarnego (Re<<1) formułuje się prawo podobieństwa przepływu: przepływy o różnych prędkościach, lepkościach i gęstościach są podobne, jeżeli ich liczby Reynoldsa są równe.
Dla przepływu laminarnego stosuje się prawo Stokes'a. Siła oporu „lepkiego”, dla cieczy opływającej ciało, przedstawia się:
|
η- współczynnik lepkości cieczy v- prędkości przepływu r- promień kulki |
|
Rozpatrując ruch kulki w cieczy, przy uwzględnieniu wszystkich działających na nią sił (zgodnie z II Zasadą Dynamiki Newtona) otrzymamy:
|
|
|
Rozwiązując powyższe równanie różniczkowe, otrzymujemy:
![]()
Poniżej prezentujemy wykres zależności prędkości od czasu:
|
Prędkość graniczna, do której dąży prędkość kulki w cieczy, wyraża się wzorem:
|
W naszym przypadku, gdy ścianki naczynia wpływają na ruch kulki w płynie, współczynnik K ze wzoru Stokes'a będzie się wyrażał, jako: K= 6πηr(1+2,4(r/R). W ostateczności lepkość cieczy badanych w naszym doświadczeniu wyraża się przez:
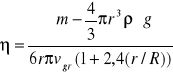
Wykonanie doświadczenia
Ćwiczenie miało na celu wyznaczenie współczynników lepkości gliceryny i oleju silnikowego.
Przed przystąpieniem do pomiarów czasu przepływu kulek w cieczy, zważyliśmy kulki za pomocą wagi laboratoryjnej oraz zmierzyliśmy ich średnicę. Następnie przystąpiliśmy do wykonania doświadczenia. Kulki zanurzaliśmy w cieczy, wypełniającej szklane rury, i za pomocą stopera mierzyliśmy czas, w jakim przebędą drogę 80cm. Punkt, od którego mierzyliśmy czas, przyjęliśmy zgodnie z sugestią Prowadzącego ćwiczenie w odległości 20 cm od powierzchni cieczy (gdybyśmy mierzyli czas od „lustra”, wówczas wynik pomiaru byłby zbyt niedokładny- początkowo, bowiem kulka porusza się ruchem opóźnionym, zgodnie z wykresem a, gdy v0>0). Na podstawie zmierzonych czasów opadania kulek oraz długości przebytej drogi, wyznaczyliśmy prędkość graniczną. Następnie wyznaczyliśmy współczynniki lepkości cieczy.
W naszym doświadczeniu badaliśmy dwie ciecze:
płyn |
gęstość ρ[g/cm3] |
średnica rury [mm] |
gliceryna |
1,473 |
28,4 |
olej silnikowy |
0,867 |
28,2 |
Poniżej przedstawiamy wyniki pomiarów masy i średnicy kulek oraz czasów opadania:
Nr |
m [mg] |
D [mm] |
l [cm] |
tgliceryna |
tolej |
1 |
179 |
3,51 |
80 |
16,5 |
6,44 |
2 |
110 |
2,98 |
80 |
20,75 |
8,53 |
3 |
109 |
2,98 |
80 |
21,07 |
8,41 |
4 |
109 |
2,98 |
80 |
20,75 |
8,46 |
5 |
111 |
2,98 |
80 |
20,94 |
8,47 |
6 |
178 |
3,51 |
80 |
15,72 |
6,44 |
7 |
111 |
2,98 |
80 |
20,66 |
8,38 |
8 |
64 |
2,48 |
80 |
28,03 |
11,22 |
9 |
63 |
2,48 |
80 |
27,91 |
11,25 |
10 |
63 |
2,48 |
80 |
27,72 |
11,34 |
11 |
111 |
2,98 |
80 |
20,31 |
8,20 |
12 |
63 |
2,48 |
80 |
27,59 |
11,25 |
13 |
179 |
3,51 |
80 |
14,94 |
6,41 |
Niemal wszystkie kulki poruszały się asymetrycznie względem osi cylindra, co wpływało na czas opadania kulek.
droga [cm] |
tgliceryna[s] |
tolej [s] |
10 |
1,88 |
0,62 |
15 |
3,16 |
1,00 |
20 |
3,91 |
1,36 |
25 |
4,78 |
1,87 |
30 |
6,25 |
2,41 |
35 |
|
2,94 |
Drugim etapem naszego ćwiczenia było wyznaczenie prędkości granicznej dla gliceryny i oleju silnikowego. Osuszone i wyczyszczone kulki wpuszczaliśmy ponownie do cylindra, mierząc tym razem czas opadania od powierzchni do wyznaczonej przez nasz zespół głębokości. Pomiarów dokonaliśmy dla kulek o D=2,98. Otrzymaliśmy następujące wyniki:
Następnie przeszliśmy do obliczenia współczynników lepkości gliceryny współczynników oleju silnikowego oraz sporządziliśmy wykres prędkości współczynników zależności od czasu współczynników początkowej fazie ruchu.
Obliczenie współczynników lepkości cieczy, rachunek błędów oraz odpowiednie wykresy znajdują się na załączonych do sprawozdania stronach.
Wnioski:
Doświadczenie przebiegło bez problemów. Nasz zespół w czasie ćwiczenia, oprócz wiedzy teoretycznej, zdobył wiedzę praktyczną, m.in. umiejętność korzystania z wagi laboratoryjnej oraz przeprowadzania pomiarów za pomocą śruby mikrometrycznej. Zgodnie z naszymi przewidywaniami współczynnik lepkości gliceryny okazał się kilkakrotnie większy niż oleju silnikowego. Wielkość błędów była uwarunkowana wieloma czynnikami, m.in.:
- niestabilnością wagi podczas ważenia kulek- każde oparcie się o stół, na którym stała waga, zmieniało wartość pomiaru, dlatego przyjęliśmy duży błąd (0,5 mg) w stos. Do dokładności wagi
- słabym refleksem eksperymentatora, mierzącego czas opadania kulek
- asymetrią opadania kulek w cylindrze
- chwilową asymetrią ośrodka (cieczy)- ponieważ wraz z kulkami z zaworu bezpieczeństwa/ wylotowego, wypływała pewna ilość cieczy, którą z powrotem wlaliśmy do cylindra, aby poziom cieczy był ~stały
F
v
Fo
S
x
y
∆y
∆v
mg
Fw+Fo
v
vo
vgr
a
b
t
l
kran
lejek
2r
Wyszukiwarka
Podobne podstrony:
lepkosc, Studia, Pracownie, I pracownia
Wyznaczanie współczynnika lepkości metodą Stokesa, Studia, Pracownie, I pracownia
Badanie wahadła skrętnego, Studia, Pracownie, I pracownia, 7 Badanie drgań wahadła skrętnego {torsyj
24 - oddane 21.04.2010, Studia, Pracownie, I pracownia, 24 Wyznaczenie mechanicznego równoważnika ci
Wstęp 59, Studia, Pracownie, I pracownia, 59 Rezonans elektromagnetyczny, Waldek
m5 NP, Studia, Pracownie, I pracownia
OSCYLOSK, Studia, Pracownie, I pracownia, 51 Pomiary oscyloskopowe, Ludwikowski
Wstęp teoretyczny 32, Studia, Pracownie, I pracownia
Sprawozdanie M7w, Studia, Pracownie, I pracownia
25, Studia, Pracownie, I pracownia, 25 Wyznaczanie współczynnika rozszerzalności cieplnej metali za
76, Studia, Pracownie, I pracownia, 76 Rozpady promieniotwórcze
teor 76, Studia, Pracownie, I pracownia
ZAGADN1, Studia, Pracownie, I pracownia, 1 Dokładność pomiaru długości, Marek
cw30, Studia, Pracownie, I pracownia, 30 Wyznaczanie względnej gęstości cieczy i ciał stałych, Ludwi
Sprawozdanie 49, Studia, Pracownie, I pracownia, 49 Charakterystyka tranzystora, Waldek
Wstęp teoretyczny 1, Studia, Pracownie, I pracownia
Instrukcja, Studia, Pracownie, I pracownia, 76 Rozpady promieniotwórcze
M5 BS, Studia, Pracownie, I pracownia
więcej podobnych podstron