Wstęp teoretyczny 1

Błąd pomiaru jest to odstępstwo wyniku jednostkowego pomiaru od wartości prawdziwej, której wielkości na ogół nie znamy. Błąd pomiaru jest bezpośrednio związany z metodą pomiaru. Wykonując pomiary nawet tym samym przyrządem otrzymamy często różne wyniki.

Błąd systematyczny - błąd wynikający z zastosowanej metody pomiaru lub innych przyczyn (np. nie dających się wykluczyć, ale znanych zjawisk mających wpływ na pomiar, zwykle zmieniający wyniki pomiaru jednostronnie. Może być spowodowany użyciem niedokładnego przyrządu pomiarowego, różnicami pomiędzy realnym układem i wyidealizowanym modelem aparatury, a także zaniedbaniem niektórych efektów w teorii badanego zjawiska.

Błąd przypadkowy występuje on tylko w przypadku serii pomiarowej, to znaczy przy wykonaniu kilku

(co najmniej dwóch) pomiarów tej samej wielkości. Źródłem błędów przypadkowych jest natura mierzonego obiektu

(niedokładność wykonania, zmieniające się warunki pomiarowe) oraz niedoskonałość naszych zmysłów.

Występowanie błędów przypadkowych powoduje, że wyniki kolejnych pomiarów zmieniają się w sposób losowy, mimo że mierzona jest ta sama wielkość w warunkach praktycznie niezmiennych. Można je modelować przy pomocy rozkładów statystycznych przykładowo rozkładu normalnego (Gaussa).

Błąd względny jest bezwymiarowy, najczęściej wyrażany w procentach

i nazywany jest wówczas błędem procentowym. Jeśli błąd jest bardzo mały, używa się również promili. Mówiąc o błędzie względnym nie sposób wspomnieć o błędzie bezwzględnym, gdyż one są bezpośrednio ze sobą związane. Błąd bezwzględny D jest różnicą miedzy wynikiem pomiaru x a wartością prawdziwą
wielkości mierzonej v, czyli D= x-v
Błąd bezwzględny D, zawsze wyrażany w jednostkach wielkości mierzonej, ma konkretny znak: plus (+) lub minus (-).

Błąd względny umożliwia porównanie dokładności przyrządów pomiarowych różnych typów o różnych zakresach.

W ogólnym przypadku wynik pomiaru przedstawiamy w postaci:

          X_R  =  X_M   ±   ΔX

gdzie: 

     X_r     - wartość rzeczywista wielkości mierzonej,

     X_M    - wartość uzyskana w wyniku pomiaru,

     ΔX    - niepewność lub błąd pomiaru. 
 

Powyższy zapis oznacza, że: 

- najlepszym przybliżeniem wartości  mierzonej jest według eksperymentatora liczba X_M ;

- z rozsądnym prawdopodobieństwem szukana wartość znajduje się gdzieś  pomiędzy  

   X_m - ΔX   i    X_m + ΔX. 
 

- Błąd pomiaru  ΔX  jest wielkością oszacowaną, więc obliczone wartości  X_m   i   ΔX  podajemy zaokrąglone. Oznacza to, że przybliżamy wartości otrzymane z obliczeń. 
 

- Cyframi znaczącymi danej liczby różnej od zera nazywamy wszystkie jej cyfry z  wyjątkiem

   występujących na początku zer.

   Do cyfr znaczących zalicza się również zera końcowe, jeśli są one wynikiem obliczeń, a nie

   zaokrągleń. Oznacza to, że pierwsza liczba znacząca musi być różna od zera, natomiast

   druga, trzecia i dalsze mogą być zerami. 
 

- Przy zaokrąglaniu wyniku pomiaru stosowane są powszechnie przyjęte zasady zaokrągleń:

- liczbę kończącą się cyframi  0-4  zaokrąglamy w dół, a 5 - 9  w górę

 

- Oszacowane błędy zaokrąglamy zawsze w górę, ponieważ w żadnym przypadku nie wolno

   zmniejszać błędów. Zawsze lepiej podać zawyżoną wartość błędu niż go niedoszacować.
  

- Obliczenia wykonujemy zawsze z większą liczbą cyfr, niż chcemy podać wynik.

   Zaokrągleń dokonujemy dopiero po zakończeniu obliczeń.
    

Niepewność standardowa pomiaru - niepewność wyniku pomiaru wyrażona w formie odchylenia standardowego (estymaty odchylenia standardowego). Oznaczana zwykle jako u_c (y).Należy zwrócić przy tym uwagę, że niepewność standardowa może być związana nie tylko z wynikiem pomiaru ale także z każdą estymatą parametru prawdopodobieństwa zmiennej losowej.

Ogólnie niepewność standardową (w zależności od sposobu jej obliczania lub szacowania) można podzielić na dwa rodzaje:

• niepewność standardową typu A, gdy jest bardzo dużo pomiarów
  

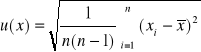
• niepewność standardową typu B, gdzie wyniki pomiarów nie wykazują rozrzutów czyli x₁=x₂=…x, lub gdy jest tylko jeden wynik

Przy pomiarach rzeczywistego zjawiska fizycznego występuje zwykle kilka źródeł niepewności pomiaru i dlatego niepewność standardowa całkowita pomiaru (oznaczana jako u_c) jest zwykle złożona z kilku pojedynczych niepewności standardowych pomiaru. Przy czym nie jest to prosta suma algebraiczna. Do szacowania współczynnika oddziaływania danej niepewności standardowej na złożoną niepewność standardową całkowitą używa się praw propagacji niepewności (przeważnie jest to rachunek różniczkowy zależny od funkcji równania opisującego mierzone zjawisko). W przypadkach szacunku uproszczonego jest to zwykle pierwiastek sumy kwadratów niepewności standardowych (pomnożonych przez oszacowane współczynniki ich wpływu na niepewność całkowitą).

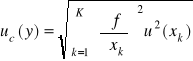
(dla nieskorelowanych x_k),

K - liczba wielkości mierzonych bezpośrednio

Regresja liniowa jest to metoda estymowania wartości oczekiwanej zmiennej y przy znanych wartościach innej zmiennej lub zmiennych x. Szukana zmienna y jest tradycyjnie nazywana zmienną objaśnianą, lub zależną. Inne zmienne x nazywa się zmiennymi objaśniającymi lub niezależnymi. Zarówno zmienne objaśniane, jak i objaśniające, mogą być wielkościami skalarnymi lub wektorami.

Regresja w ogólności to problem estymacji warunkowej wartości oczekiwanej. Regresja liniowa jest nazywana liniową, gdyż zakładanym modelem zależności między zmiennymi zależnymi, a niezależnymi, jest funkcja liniowa. Prosta regresji jest to prosta o równaniu

y = ax + b

jak najlepiej dopasowana do zbioru n punktów doświadczalnych (x₁, y₁), (x₂, y₂), ... (x_n, y_n). Celem dopasowania jest nie tylko uzyskanie efektu wizualnego, ale przede wszystkim uzyskanie ocen wartości parametrów a i b opisujących prostą, oraz ich niepewności u(a) i u(b). Najczęściej wykorzystujemy do tego celu metodę najmniejszych kwadratów. Najpowszechniejszy wariant tej metody, stosowany jest gdy niepewności przypisane punktom eksperymentalnym są jednakowe.

---