Badanie odbicia światła od powierzchni dielektryków.

1.Wstęp teoretyczny

Falą elektromagnetyczną nazywamy rozchodzące się zaburzenie wzajemnie przenikających się zmiennych pól magetycznego i elektrycznego. Światło jest przykładem takiej fali. Najprostszą do opisu falą jest fala monochromatyczna tzn. zaburzenie okresowe o częstości . Wielkościami opisującymi falę elektromagnetyczną są wektory natężeń pól elektrycznego i magnetycznego. Natężenie pola elektrycznego i magnetycznego w dowolnym punkcie prze -strzeni zmienia się w czasie proporcjonalnie do funkcji cos( t ) i osylacje te przesuwają sie ze stałą prędkością .Wartość zaburzenia przesunie się o x dopiero po upływie czasu t =
, czyli w chwili t oscylacje są w punkcie x soą opóźnione względem oscylacji w punkcie x=0

i wynoszą :

cos[(t-t)]=cos( t -kx ),

dlatego też wektor natężenia pola elektrycznego fali monochromatycznej opisywany jest wzo -rem:
, gdzie
jest amplitudą natężenia pola elektrycznego

t -kx jest fazą fali

k=
jest liczbą falową

Wartość pola magnetycznego zmienia się w analogiczny sposób.Ponieważ częstość jest bar -dzo duża, a nie istnieją detektory reagujące na tak szybkie zmiany natężenia pola elektrycznego,

dlatego też wielkością opisującą falę świetlną jest natężenie światła I. Natężnie światła jest

proporcjonalne do kwadratu amplitudy natężenia I~
. Pola elektryczne i magnetyczne są

opisywane przez wektory więc należy określić także ich kierunek. Wektory natężenia tych pól

są względem siebie prostopadłe i porstopadłe do kierunku rozprzestrzeniania się fali. Wyz -naczenie kierunku rozprzestrzeniania się fali nie wyznacza jeszcze dokładnie kierunków wek -

torów natężenia tych pól. Dokładne określenie kierunku tych wektorów wiąże się z pojęciem

polaryzacji.

2.Polaryzacja

Polaryzacją możemy nazwać uporządkowanie wektorów natężenia pól elektrycznego i mag -

netycznego pod względem kierunku tzn. kierunek drgań wektora natężenia pola elektrycznego

i prostopadłego do niego pola magnetycznego jest stały i jednakowy dla wszystkich punktów

na drodze rozchodzenia się fali. Wtedy możemy mówić o polaryzacji liniowej, jednakże wekto -

mogą obracać się wokół kierunku rozchodzenia się fali: wtedy mówimy o polaryzacji kołowej

lub ogólniej eliptycznej.Każdy stan polaryzacji moża uzyskać przez nałożenie dwóch fal spola -

ryzowanych liniowo o odpowiednio dobranej różnicy faz. Do wytwarzania i badania swiatła

spolaryzowanego służą polaryzatory: elementy przepuszczające światło o danym kierunku polaryzacji. Światło niespolaryzowane po przejściu przez polaryzator będzie spolaryzowane w kierunku przepuszczanym przez polaryzator(kierunek ten nazywamy osią polaryzatora).

Gdy oświetlimy polaryzator światłem spolaryzowanym liniowo to przejdzie ono w całości gdy

kierunek polaryzacji pokrywa się z osią polaryzatora, lub gdy kierunek polaryzacji tworzy kąt ,

to jest przepuszczana część fali określona przez rzut wektora natężenia pola fali elektromagne -

tycznej na kierunek osi polaryzatora. Natężenie światła jest proporcjonalne do kwadratu amplitudy, więc natężenie przechodzącego światła przez polaryzator wynosi:

I =
cos2 ,

gdzie
jest natężeniem światła spolaryzowanego liniowo. Jest to tzw. prawo Malusa. Prawo

Malusa jest spełnione tylko dla światła spolaryzowanego liniowo( natężenie jest zależne od ką -ta ). Pomiary wykonane do sprawdzenia prawa Malusa są zebrane w tabeli.

Kąt	Natężenie prądu w [mA]
	Obracny analizator	Obracany polaryzator
0	4	4
15	3.8	3.6
30	3.4	3.2
45	2.7	2.4
60	1.6	1.4
75	0.6	0.5
90	0	0

Z wyliczeń teoretycznych wynika że natężenie przechodzącego światła zmaleje dwukrotnie

gdy obrócimy polaryzator lub analizator o kąt 45, z naszych danych doświadczalnych wynika,

że natęzenie zmaleje o połowę przy kącie większym od 45.Niedokładności pomiarów wynikają z błędu odczytu fotoprądu, klasy amperomierza, wpływu światła zewnętrznego. Poza tym polaryzatory nie są idealne i przepuszczają częściowo światło o kierunku polaryzacji innym niż określonym przez oś polaryzatora.

Przepuszczając spolaryzowane światło przez koloidalną zawiesinę (w naszym doświadczeniu była to herbata ) zaobserwowaliśmy, że wiązka rozproszona była niewidoczna w kierunku osi polaryzacji. Wynika to z faktu że, że fala elektromagnetyczna jest falą poprzeczną i stąd nie moze sie rozchodzic w kierunku drgań nateżenia pola elektrycznego.

3.Całkowite wewnętrzne odbicie

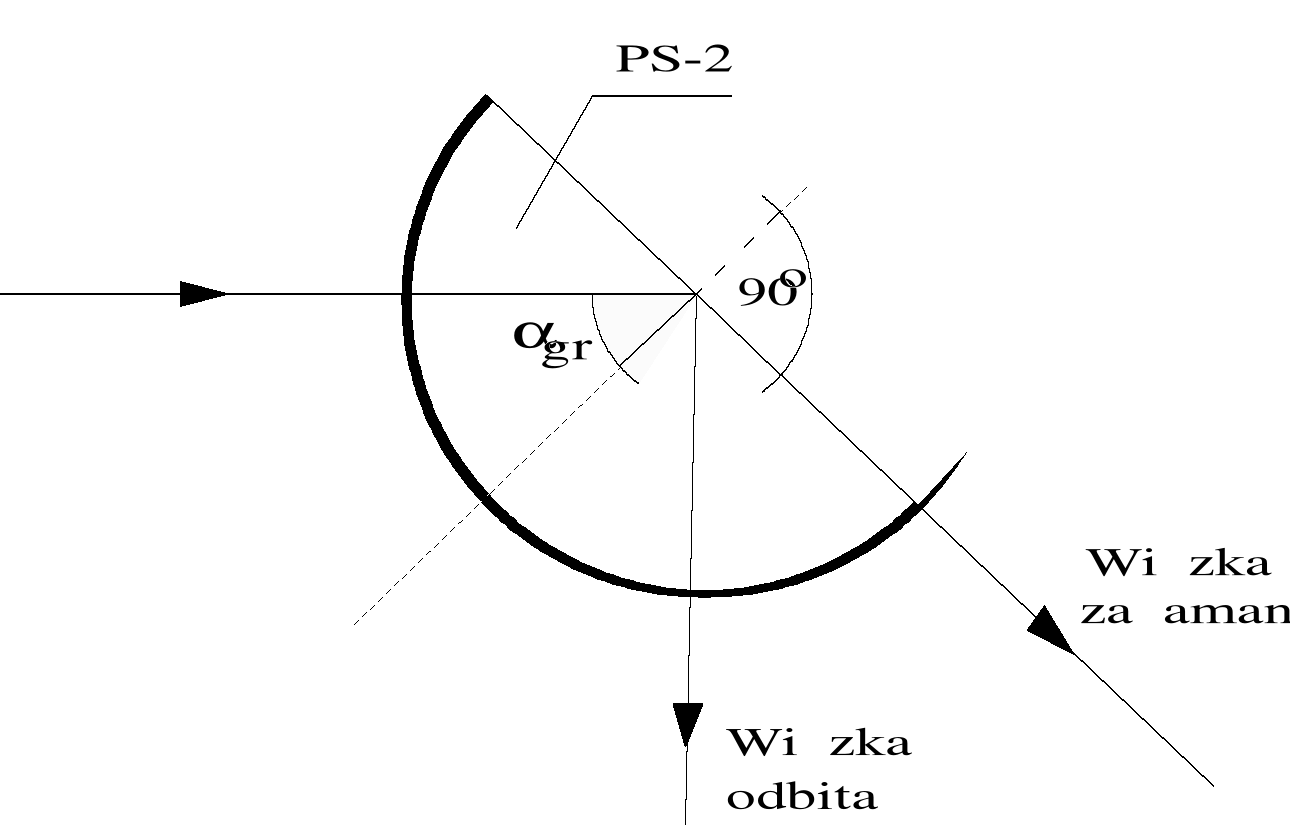
Zauważylismy także że, wiązka światła padająca na granicę płytka szklana (PS2) - powietrze ulega odbiciu. Przy odpowiednim kącie padania (gr ) możemy zaobserwować zjawisko całkowitego wewnęrznego odbicia, które polega na tym, ze zanika wiązka załamana. Kat pod jakim zachodzi to zjawisko nazywamy kątem granicznym. Korzystając z prawa załamania Snelliusa :

Wiemy, że =90 więc

singr =
, gdzie n1 współczynnik załamania dla powietrza

n2 współczynnik załamania dla substancji

Przyjmując, że współxczynnik załamania dla powietrza jest równy 1otrzymujemy, że

n2 =

Pozwala nam to obliczyć współczynnik załamania danej substancji. W naszym wypadku kąt graniczny wyniósł 43( 0.75 rad). Podstawiając do otrzymujemy wartość współczynnika

n2 = 1.47

Rachunek błędów:

Korzystamy z metody różniczki zupełnej.Wobec tego

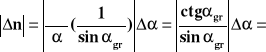
=0.017 rad

n=0.04

Współczynnik załamania substancji wynosi

n = 1.47 0.04

4.Polaryzacja przez odbicie

Układ doświadczalny

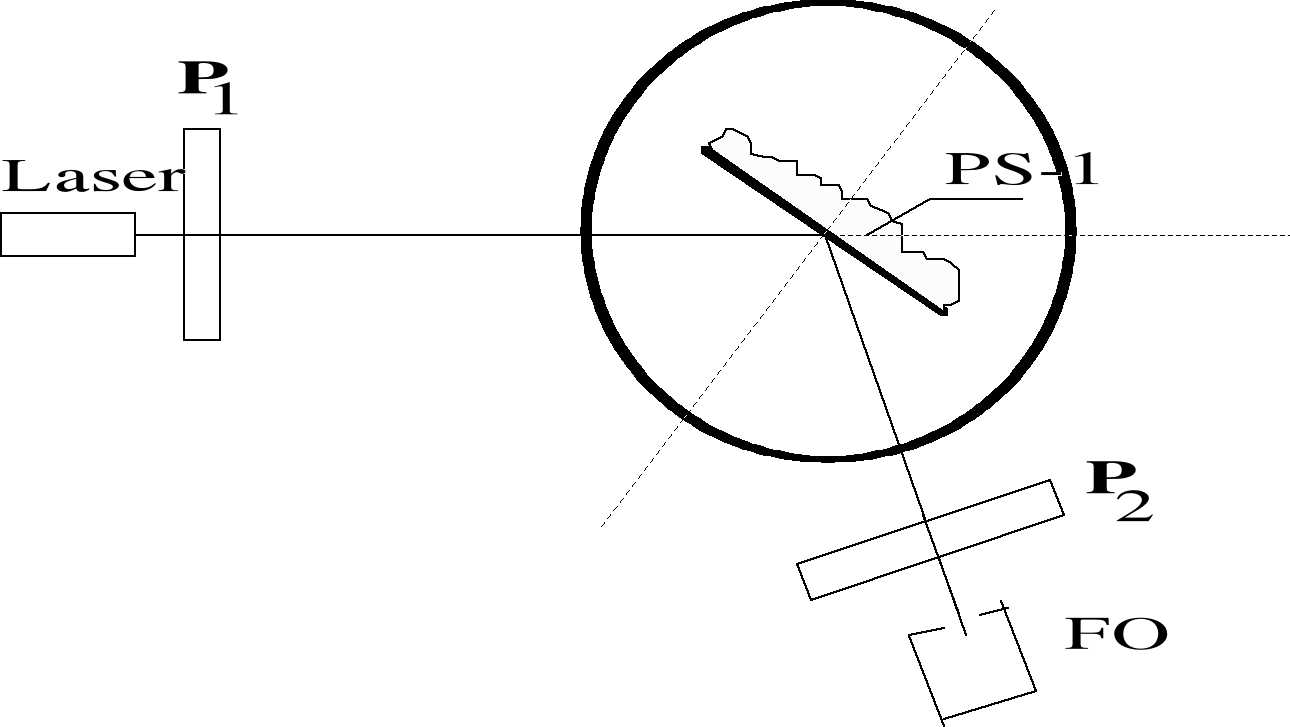
W dalszej części ćwiczenia obserwowaliśmy odbicie na granicy powietrze - płytka szklana. Oprócz tego mierzyliśmy natężenie fotoprądu. Wyniki podane w tabeli przedstawiają zależność natężenia prądu dla wiązki spolaryzowanej w płaszczyźnie równoległej do płaszczyzny podania.

Pomiary natężenia prądu w zależności od kąta padania
Odbicie na granicy powietrze - szkło
Kąt padania	Natężenie prądu [A]
90	3200
85	1500
80	1100
75	600
70	200
65	45
6230	18
60	4
57	1.8
56.2	0
55	0.7
50	5.8
45	16
40	32
35	46
30	58
25	68
20	74
15	74

Przy kącie padania równym 56.2o nastąpił zanik wiązki odbitej: kąt ten nazywamy kątem Brewstera. Jest to kąt dla którego suma kątów podania i załamania równa się 90o. Ze wzorów Fresnela wynika ze dla (+)=90o
równa się zero.

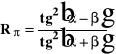
(1) ,
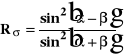
(2)

gdzie,
-współczynnik odbicia dla polaryzacji podającej w płaszczyźnie padania,

-współczynnik odbicia dla polaryzacji prostopadłej do płaszczyzny padania,

-kąt padania, -kat załamania.

Warunek na kąt Brewstera jest następujący:

tgB=
, gdzie n1 współczynnik załamania dla powietrza

n2 współczynnik załamania dla substancji

Przyjmując współczynnik załamania dla powietrza równy 1 otrzymujemy:

tgB = n2

W naszym przypadku kąt Brewstera wynosi

B = 56.2

Dla tego kąta współczynnik załamania wynosi

n2 = 1.49

Rachunek błędów:

B=0.07 rad

,gdzie B -zostało wyznaczone z dołączonego wykresu,

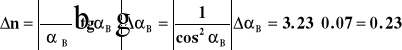
n=0.23

Współczynnik załamania substancji wynosi

n = 1.49 0.23

Współczynnik załamania wyliczony za pomocą kąta Brewstera pokrywa się z wyliczeniami wcześniejszymi (wyliczony za pomocą kąta granicznego, gdzie n = 1.47 0.04). Możemy z tego wywnioskować, że rzeczywiste n oscyluje w granicach błędu z naszymi wyliczeniami.

Wszystkie obliczenia zostały wykonane za pomocą kalkulatora.

---