JEDNOOKRESOWY MODEL DWUMIANOWY

Wycena opcji na akcję związana jest z konstruowaniem tzw. drzewa dwumianowego. Drzewo to przedstawia poziomy cenowe, jakie może osiągnąć akcja w okresie ważności opcji. Przedstawimy jednookresowy model dwumianowy.

Zacznijmy od przykładu liczbowego, w którym wiadomo, że za trzy miesiące cena akcji, kształtująca się obecnie na poziomie 20 dola­rów, wyniesie 22 lub 18 dolarów. Załóżmy, że interesuje nas wycena europejskiej opcji kupna powyższych akcji z ceną wykonania 21 dola­rów i terminem do wygaśnięcia 3 miesiące. Jeśli na koniec tego okresu cena akcji osiągnie 22 dolary, to wartość opcji będzie równa l dolar. Jeśli natomiast cena akcji spadnie do 18 dolarów, wartość opcji będzie zerowa. Spróbujmy przedstawić to na diagramie:

Cena akcji = 22 $

Cena opcji = 1 $

Cena akcji = 20 $

Cena akcji = 18 $

Cena opcji = 0 $

Niezbędnym założeniem jest to, że inwestor nie ma możliwości dokonywania korzystnych transakcji arbitrażowych. Konstruujemy port­fel składający się z akcji i opcji. Ponieważ z portfelem tym nie jest związane żadne ryzyko, jego stopa zwrotu musi być równa wolnej od ryzyka stopie procento­wej. Umożliwia to określenie kosztów utworzenia portfela, a więc ceny opcji. Jako że mamy do czynienia tylko z dwoma papierami wartościo­wymi (jedną akcją i jedną opcją na akcję) oraz z dwoma potencjalnymi wielkościami dochodu z portfela, zawsze istnieje możliwość określenia portfela wolnego od ryzyka.

Rozważmy portfel składający się z Δ akcji (w pozycji długiej) oraz jed­nej opcji kupna (w pozycji krótkiej). Inwestor chce się zabezpieczyć przed tańszą sprzedażą. Obliczymy wartość parametru Δ, dla którego utworzony portfel będzie wolny od ryzyka. Jeśli cena ak­cji wzrasta z 20 do 22, to wartość posiadanych akcji jest równa 22Δ, a wartość opcji 1. Wynika z tego, że całkowita wartość portfela wyno­si 22Δ - l. Jeśli zaś cena akcji spada z 20 do 18, to wartość akcji wyno­si 18Δ, a wartość opcji jest zerowa. W związku z tym wartość całego portfela musi być równa 18Δ. Ryzyko opisanego portfela będzie równe zeru, jeśli Δ zostanie dobrana w taki sposób, aby końcowa wartość portfela była taka sama dla obu rozważanych alternatywnych cen akcji. Oznacza to, że:

22Δ - 1 = 18Δ

czyli:

Δ= 0,25.

W ten sposób wolny od ryzyka portfel będzie się składał z:

Pozycji długiej: 0,25 akcji.

Pozycji krótkiej: l opcji.

Jeśli cena akcji wzrasta do 22, to wartość takiego portfela jest równa:

22×0,25-1 = 4,5

jeśli zaś cena spada do 18, to wartość tego portfela wyniesie:

18×0,25 = 4,5

Jak zatem widać, niezależnie od tego, czy cena akcji rośnie, czy spada, wartość całego portfela w chwili wygaśnięcia opcji jest zawsze równa 4,5.

Gdy korzystny arbitraż nie jest możliwy, stopa zwrotu z portfela wol­nego od ryzyka musi być równa wolnej od ryzyka stopie procentowej. Załóżmy, że w naszym przykładzie wolna od ryzyka stopa procentowa wynosi 12 procent w skali rocznej. Uwzględniając to możemy stwier­dzić, że wartość portfela w dniu dzisiejszym wynosi:

4,5
= 4,367

Aktualna cena akcji jest znana i wynosi 20. Jeśli założymy, że cena opcji oznaczona jest jako f, to wartość portfela w dniu dzisiejszym możemy zapisać jako:

20×0,25 -
= 5 -

Z tego zaś wynika, że:

5 -
= 4,367,

czyli:

= 0,633

Powyższe obliczenia pokazują, że tam, gdzie arbitraż jest niemożliwy, obecna wartość opcji musi być równa 0,633 dolara. Gdyby cena opcji była wyższa niż 0,633, to koszt konstrukcji portfela byłby niższy aniżeli 4,367, a stopa zwrotu z portfela wyższa niż wolna od ryzyka stopa pro­centowa. Analogicznie, jeśli cena opcji byłaby niższa aniżeli 0,633, to sprzedaż całego portfela umożliwiałaby pożyczenie środków na procent niższy od wolnej od ryzyka stopy procentowej.

Uogólnienie

Aby uogólnić wnioski z przedstawionego powyżej przykładu, rozważ­my przykład akcji, której cena jest równa S, i opcji na akcję kosztującej obecnie f. Zakładamy, że okres do terminu wygaśnięcia opcji wynosi T, a w okresie ważności opcji cena akcji może wzrosnąć od S do Su, bądź spaść od S do Sd (u > 1, d < 1). W razie wzrostu ceny akcji do poziomu Su zakładamy, że dochód z opcji wynosi
, zaś w razie jej spadku do poziomu Sd wynosi
.

Su

S

Sd

Podobnie jak poprzednio, wyobraźmy sobie portfel składający się z Δ akcji (długa pozycja) i 1 opcji (krótka pozycja). Obliczmy wartość Δ, dla której portfel ten jest wolny od ryzyka. W razie wzrostu ceny akcji wartość portfela w momencie wygaśnięcia opcji jest równa:

SuΔ -

Jeśli natomiast cena akcji spada, wartość naszego portfela w tym samym momencie wyniesie:

SdΔ -

Wartości te są sobie równe, gdy:

SuΔ -
= SdΔ -

czyli:

Δ =

W takim wypadku portfel jest wolny od ryzyka. Wartość Δ jest równa stosunkowi zmiany ceny opcji, do zmiany ceny akcji pomiędzy dwoma węzłami drzewa dwumianowego.

Jeśli wolną od ryzyka stopę procentową oznaczymy jako r, to wartość bieżąca rozpatrywanego portfela musi być równa:

a koszt skonstruowania portfela wynosi:

SΔ -

Z tego wynika, że:

SΔ -
=

Jeśli w powyższym równaniu za Δ podstawimy
, to otrzymamy:

=
=
=
=

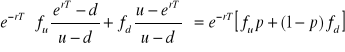
Więc otrzymujemy:

gdzie:

p =
1 - p =

Wzory te stwarzają możliwość wyceny opcji przy użyciu jednookresowego modelu dwumianowego.

W rozpatrywanym poprzednio przykładzie liczbowym mieliśmy do czynienia z następującymi wartościami zmiennych: u =
= 1,1; d =
= 0,9; r = 0,12; T =
= 0,25; f_u=l; f_d = 0. Stąd otrzymujemy wartość:

zaś wartość opcji możemy obliczyć podstawiając do wzoru:

Jak widać, otrzymane wartości są takie same jak w podanym przykładzie.

Szukasz gotowej pracy ?

To pewna droga do poważnych kłopotów.

Plagiat jest przestępstwem !

Nie ryzykuj ! Nie warto !

Powierz swoje sprawy profesjonalistom.

---