WERYFIKACJA HIPOTEZ STATYSTYCZNYCH
Jest to druga metoda wnioskowania statystycznego.
Hipoteza statystyczna - jest to jakiekolwiek przypuszczenie dotyczące rozkładu zbiorowości statystycznej.
Dokonując weryfikacji postawionej hipotezy rozstrzygamy o jej słuszności. Weryfikacja hipotez odbywa się przy wykorzystaniu testów statystycznych, które określa się jako testy istotności. Sprawdzanie słuszności postawionej hipotezy odbywa się przy założonym z góry prawdopodobieństwie popełnienia błędu, określa się je mianem poziomu istotności i oznacza przez α. Przyjmuje się, że α jest to prawdopodobieństwo nie większe od 0,10.
Algorytm postępowania przy weryfikacji hipotez:
Formalne i merytoryczne sformułowanie hipotez
Na tym etapie stawiamy dwie hipotezy, a mianowicie:
H0 - hipoteza zerowa czyli hipoteza której słuszność sprawdzamy, przyjmuje ona zawsze postać równości (np. H0: E(x) = 150
H1 - hipoteza alternatywna która jest konkurencyjna w stosunku do hipotezy zerowej, może ona mieć jedną z trzech postaci:
H1: E(x) ≠150
H1: E(x) >150
H1: E(x) <150
Stawiając tę hipotezę wybieramy oczywiście jedną z tych trzech postaci tej hipotezy.
Zakładamy poziom istotności przy którym weryfikujemy hipotezę zerową H0.
Ze zbiorowości losujemy próbę (może to być próba duża n>30, bądź mała n≤30) i dla tej próby ustalamy potrzebne parametry statystyczne (to jakie parametry liczymy zależy od testu który stosujemy, czyli od tego jaką hipotezę weryfikujemy)
Na podstawie wyników uzyskanych z próby liczymy tzw. statystykę empiryczną temp
Z odpowiednich tablic odczytujemy statystykę teoretyczną tteor
Porównujemy obie statystyki tzn temp z tteor . Na podstawie porównania podejmujemy decyzję bądź o słuszności hipotezy zerowej bądź o konieczności odrzucenia H0 i przyjęcia w jej miejsce hipotezy alternatywnej.
Z reguły porównując obie statystyki rozrysowuje się tzw. obszar krytyczny. Można jednak dokonać porównania bez rozrysowywania obszaru krytycznego (jest to uproszczony sposób podejmowania decyzji przy weryfikacji)
Jeżeli: |temp|≥tteor - odrzucamy hipotezę zerową i przyjmujemy alternatywną
Jeżeli : |temp|< tteor - stwierdzamy brak podstaw do odrzucenia hipotezy zerowej
Ta procedura ma zastosowanie do wszystkich rodzajów testów istotności, zawsze weryfikując hipotezę trzymamy się tej procedury.
Weryfikacja dla średniej arytmetycznej (wartości przeciętnej)
Procedura:
Formalne i merytoryczne sformułowanie hipotez
Na tym etapie stawiamy dwie hipotezy, a mianowicie:
H0: E(x) = 150
H1: E(x) ≠150
H1: E(x) >150
H1: E(x) <150
Stawiając tę hipotezę wybieramy oczywiście jedną z tych trzech postaci tej hipotezy.
Np.
H0: E(x) = 150
H1: E(x) ≠150
Czyli hipoteza zerowa zakłada że średnia wartość w całej zbiorowości wynosi 150, a hipoteza alternatywna zakłada, że jest ona różna od 150
Zakładamy poziom istotności przy którym weryfikujemy hipotezę zerową H0.
Np. α = 0,10
Ze zbiorowości losujemy próbę (może to być próba duża n>30, bądź mała n≤30) i dla tej próby ustalamy potrzebne parametry statystyczne - przy weryfikacji hipotezy dla średniej arytmetycznej musimy policzyć ale próby średnią arytmetyczną oraz odchylenie standardowe
Na podstawie wyników uzyskanych z próby liczymy tzw. statystykę empiryczną temp
Dla dużej próby (n>30)
![]()
Dla małej próby (n≤30)
![]()
Z odpowiednich tablic odczytujemy statystykę teoretyczną tteor
Sposób odczytu zależy oczywiście od liczebności próby a dodatkowo od postaci hipotezy alternatywnej.
Dla dużej próby posługujemy się tablicami dystrybuanty rozkładu normalnego. Dczytujemy w następujący sposób:
H1: ≠ dla takiej postaci H1 odczytujemy 1- α/2 (czyli jeden minus poziom istotności podzielony przez 2)
H1: > Dla tych postaci sposób odczytu jest taki sam odczytujemy dla 1 - α
H1: <
Dla małej próby (n≤30) odczytujemy z tablic rozkładu studenta, sposób odczytu następujący:
H1: ≠ dla takiej postaci H1 odczytujemy dla k=n-1 oraz α
H1: > Dla tych postaci sposób odczytu jest taki sam odczytujemy dla k= n-1 oraz 2*α
H1: <
Porównujemy obie statystyki tzn temp z tteor . Na podstawie porównania podejmujemy decyzję bądź o słuszności hipotezy zerowej bądź o konieczności odrzucenia H0 i przyjęcia w jej miejsce hipotezy alternatywnej.
Z reguły porównując obie statystyki rozrysowuje się tzw. obszar krytyczny. Można jednak dokonać porównania bez rozrysowywania obszaru krytycznego (jest to uproszczony sposób podejmowania decyzji przy weryfikacji)
Jeżeli: H1 ma postać ≠ to :
|temp|≥tteor - odrzucamy hipotezę zerową i przyjmujemy alternatywną
|temp|< tteor - stwierdzamy brak podstaw do odrzucenia hipotezy zerowej
Jeżeli H1 ma postać >
temp≥ tteor to odrzucamy H0
temp< tteor brak podstaw do odrzucenia H0
Jeżeli H1 ma postać <
temp≤ - tteor to odrzucamy H0
temp> - tteor brak podstaw do odrzucenia H0
Przykład 1
Dokonując analizy przestępczości nieletnich dla wylosowanej próby zgromadzono m.in. informacje dotyczące wieku. Uzyskano następujące wyniki (wiek w latach): 17; 16; 18; 15; 17; 19; 16; 15; 17; 14; 13; 15; 16; 14; 18.
Zakładając, że rozkład wieku nieletnich przestępców ma charakter rozkładu normalnego przy poziomie istotności 0,01 zweryfikować hipotezę iż średni wiek dla całej populacji jest równy 17 lat.
Czyli mamy małą próbę n=15.
Stawiamy hipotezy:
H0: E(x) = 17
H1: E(x) ≠17
W treści mamy podany poziom istotności α=0,01
Mamy pobraną małą próbę dla której musimy policzyć średnią arytmetyczną i odchylenie standardowe.
Xi |
Xi - śred |
()^2 |
17 |
1 |
1 |
16 |
0 |
0 |
18 |
2 |
4 |
15 |
-1 |
1 |
17 |
1 |
1 |
19 |
3 |
9 |
16 |
0 |
0 |
15 |
-1 |
1 |
17 |
1 |
1 |
14 |
-2 |
4 |
13 |
-3 |
9 |
15 |
-1 |
1 |
16 |
0 |
0 |
14 |
-2 |
4 |
18 |
2 |
4 |
Suma = 240 |
|
Suma = 40 |
Średnia arytmetyczna: 240/15 = 16 lat
S(x) = 1,63 lat
Mając średnią i odchylenie standardowe liczymy statystykę empiryczną:
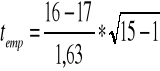
= -0,61*3,74 = -2,28
Teraz musimy odczytać statystykę teoretyczną, jest to mała próba czyli tablice rozkałdu studenta
Hipoteza alternatywna ma znak ≠więc odczytamy dla: K= n-1 oraz α
Czyli do odczytu: k= 15-1 =14 oraz α=0,01
Z tablic studenta (sposób odczytu jak przy estymacji) odczytujemy statytyke teoretyczną:
Tteor = 2,9768
Porównujemy teraz obie statystyki
|t emp|< tteor bo |-2,28|< 2,9768
2,28 < 2,9768
Czyli: Brak podstaw do odrzucenia hipotezy zerowej, czyli przy poziomie istotności 0,01 można twierdzić, że średni wiek nieletnich przestępców wynosi 17 lat.
PRZYKŁAD 2
Zebrano informacje dla grupy 400 kierowców którzy w okresie ostatnich 8 lat na terenie miasta Wałbrzych spowodowali wypadek drogowy znajdując się pod wpływem alkoholu o poziomie alkoholu we krwi (w promilach). Uzyskano średnią arytmetyczną równą 1,8 promila z odchyleniem standardowym S(x) = 0,48 promila. Zakładając, ze badana zbiorowość ma charakter rozkładu normalnego przy poziomie istotności 0,05 zweryfikować hipotezę, ze średnie stężenie alkoholu we krwi w całej populacji jest większe od 2,3 promila.
Stawiamy hipotezy:
H0: E(x) = 2,3 promila
H1: E(x) > 2,3 promila
Poziom istotności mamy już podany w treści: α = 0,05
Z populacji pobrano dużą próbę n = 400 i mamy już dla próby policzoną średnią 1,8 promila i S(X)= 0,48 promila
Liczymy statystykę empiryczną:
![]()
![]()
Teraz z tablic odczytujemy statystykę teoretyczną - duża próba więc posługujemy się tablicami rozkładu normalnego. Hipoteza alternatywna ma postać H1: E(x) > 2,3 promila więc odczytamy dla 1-α,
1-α = 1- 0,05 = 0,95 - tej warości szukamy w środkowej części tablic
Stąd tteor = 1,65
Porównujemy obie statystyki:
temp < t teor bo -20,83 <1,65
Czyli nie ma podstaw do odrzucenia hipotezy zerowej, czyli przy poziomie istotności 0,05 można twierdzić że średnie stężenie alkoholu we krwi w całej populacji wynosi 2,3 promila,
![]()
![]()
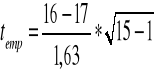
![]()
![]()
Wyszukiwarka
Podobne podstrony:
7617
7617
7617
7617
7617
7617
praca-magisterska-wa-c-7617, Dokumenty(2)
więcej podobnych podstron