Przybliżone metody chemii kwantowej

Dwie rodziny metod:

1. metody rachunku zaburzeń (metody perturbacyjne);

2. metody wariacyjne.

Metody wariacyjne

Schemat każdej metody wariacyjnej opiera się na następującym rozumowaniu:

Mamy dane równanie Schrödingera, które jest zbyt trudne (ze względu na skomplikowaną strukturę elektronową układu), aby można je było rozwiązać w sposób ścisły:

Chcemy zatem otrzymać rozwiązania (czyli energie E_n i funkcje ψ_n) w postaci przybliżonej. Najczęściej interesuje nas stan o najniższej energii, czyli stan podstawowy układu, a więc E₀ i ψ₀.

Oczywiście energie E_n wszystkich innych stanów (dla n>0) będą większe od E₀ (energii stanu podstawowego): E₀<E_n (dla n>0).

Bierzemy pewną (dowolną) funkcję φ (określoną w tej samej przestrzeni co funkcje ψ_n) i za jej pomocą definiujemy pewną wielkość ε w sposób następujący:

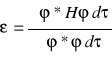
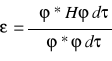
Powyższe równanie przypomina postulat o wartości średniej. Gdyby funkcja φ opisywała jakiś stan, to wartość ε byłaby równa energii układu w tym stanie (jako wartość średnia hamiltonianu).

Pomimo, iż nie znamy poprawnych funkcji własnych naszego układu, czyli ψ₀, ψ₁, ψ₂, ..., wiemy, że tworzą one układ zupełny funkcji ortonormalnych. Możemy więc przedstawić funkcję φ w postaci rozwinięcia

(*)

Zakładając, że funkcja φ jest unormowana, dostajemy:

, czyli

a zatem

Podstawiając rozwinięcie * do wyrażenia na ε i wykorzystując, że funkcja φ jest unormowana a funkcje ψ_n są ortonormalne mamy:

Ponieważ
, to możemy zapisać, że E₀ = E₀ ∙

Odejmijmy E₀ od lewej strony wyrażenia na ε oraz E₀= E₀∙

od prawej strony:

Ponieważ: (i) iloczyn c_n*∙c_n jest zawsze dodatni, (ii) E₀ jest zawsze mniejsze od E_n (gdyż E₀ reprezentuje stan o najniższej energii), to:

prawa strona powyższego równania jest zawsze nieujemna

Wobec tego lewa strona musi spełniać warunek: ε - E₀ ≥ 0

z czego natychmiast wynika, że ε ≥ E₀

Wniosek: wartość średnia ε hamiltonianu obliczona za pomocą dowolnej funkcji φ (określonej w tej samej przestrzeni) nie jest nigdy mniejsza od jego ścisłej wartości własnej E₀ , odpowiadającej stanowi podstawowemu ψ₀

(gdyby funkcja φ była ścisłą funkcją własną dla stanu podstawowego (czyli φ=ψ₀), wówczas otrzymalibyśmy ε=E₀ )

Powyższy wniosek stanowi podstawę metody wariacyjnej

Postępowanie w ramach metody wariacyjnej:

(i) wiemy, że wartość ε (obliczona dla dowolnej funkcji φ) jest zawsze większa od dokładnej wartości energii stanu podstawowego

(ii) wiemy, że jeżeli obliczymy ε dla kilku dowolnych funkcji φ₁, φ₂, φ₃, ... uzyskując odpowiednio ε₁, ε₂, ε₃, ... to najmniejsza z wartości ε_i będzie najbliższa energii stanu podstawowego;

(iii) należy zatem zminimalizować funkcjonał ε[φ], przy czym ε oznacza wartość średnią hamiltonianu obliczoną przy pomocy funkcji φ ;

(iv) bierzemy pewną funkcję próbną φ, zależącą od współrzędnych r₁, r₂, r₃, ... charakteryzujących układ, oraz od kilku parametrów liczbowych c₁, c₂, c₃, ... , czyli

φ = φ (c₁, c₂, c₃, ..., c_k ; r₁, r₂, r₃, ..., r_n)

Równanie to określa całą klasę funkcji (różniących się między sobą wartościami parametrów c₁, c₂, c₃, ..., c_k );

(v) obliczamy wartość ε (zgodnie z postulatem o wartości średniej), a wynikowa wielkość ε będzie tak naprawdę funkcją parametrów c₁, c₂, c₃, ..., c_k (czyli ε = ε (c₁, c₂, c₃, ..., c_k ) );

(vi) obliczamy minimum ε ze względu na parametry c₁, c₂, c₃, ..., c_k

(vii) uzyskana najmniejsza wartość ε_min , którą oznaczamy przez E, jest najlepszym przybliżeniem energii stanu podstawowego badanego układu, osiągalnym za pomocą funkcji φ=φ(c_i;r_i)

(viii) minimalizacja energii ε prowadzi do wyznaczenia wartości współczynników c₁, c₂, c₃, ..., c_k a więc w konsekwencji do ustalenia postaci funkcji φ = φ (c₁, c₂, c₃, ..., c_k ; r₁, r₂, r₃, ..., r_n) , która jest najlepszym przybliżeniem dokładnej funkcji falowej ψ₀

(w obrębie rozpatrywanej klasy funkcji).

Zwiększenie liczby parametrów c_i prowadzi do poszerzenia rozpatrywanej klasy funkcji a więc zwiększa dokładność wyniku.

Wniosek: uzyskanie bardzo dokładnego wyniku jest wyłącznie kwestią uwzględnienia dostatecznie dużej liczby parametrów wariacyjnych

Liniowe i nieliniowe parametry wariacyjne. Metoda Ritza.

Przykładem funkcji próbnej z parametrem nieliniowym jest np.

Ψ = N(c)∙exp(-c∙r) (r jest zmienną, N(c) to współczynnik normalizacyjny zależny od c, natomiast c jest parametrem wariacyjnym). Parametry wariacyjne nieliniowe są bardzo efektywne w sensie możliwości uzyskania stosunkowo dobrego wyniku przy zastosowaniu niewielkiej liczby takich parametrów.

Wada: nieliniowe parametry prowadzą do bardziej skomplikowanych równań (których rozwiązanie wymaga więcej czasu).

Jeżeli stosujemy liniowe parametry wariacyjne, to mówimy o tzw. metodzie Ritza (a zatem stosowanie metody Ritza polega na użyciu metody wariacyjnej z funkcją próbną zawierającą wyłącznie liniowe parametry wariacyjne). W metodzie Ritza zakładamy więc funkcję próbną postaci φ = c₁ χ₁ + c₂ χ₂ +...+ c_N  χ_N

Podstawiając powyższe rozwinięcie do równania na ε (postulat o wartości średniej) otrzymujemy:

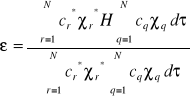
, czyli

Zdefiniujmy dwie całki:

(całkę S_rq nazywamy zazwyczaj całką nakrywania, natomiast całkę H_rq nazywamy elementem macierzowym hamiltonianu).

Wykorzystując te symbole mamy zatem:

Szukamy teraz minimum ε ze względu na współczynniki c_r* i c_q (współczynniki te są liczbami zespolonymi).

Różniczkujemy ostatnie równanie względem wybranego c_p* :

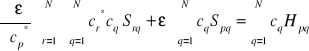
Ponieważ szukamy ekstremum ε jako funkcji c_r*, więc założymy

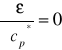
(tzn. że funkcja ε jest minimum ze względu na c_p*),

a tę minimalną wartość ε oznaczymy przez E. Otrzymujemy:

czyli

Ostatecznie:

przy czym p = 1, 2, 3, ... , N

Powyższy zapis jest de facto układem równań:

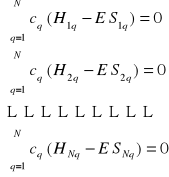
Jest to tzw. układ równań wiekowych

Układ równań wiekowych jest układem równań liniowych jednorodnych. Trywialne rozwiązanie takiego układu odpowiada sytuacji, gdy wszystkie współczynniki c_k są równe zero.

Nietrywialne rozwiązania tego układu istnieją wtedy i tylko wtedy, gdy wyznacznik zbudowany ze współczynników przy niewiadomych znika (jest równy zeru).

A zatem: warunkiem rozwiązywalności układu równań wiekowych jest znikanie wyznacznika (tzw. wyznacznika wiekowego):

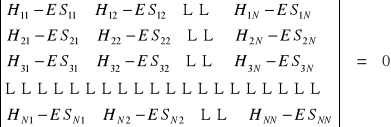
Wyznacznik wiekowy zapisujemy często w postaci skróconej:

Oczywiste jest, że po rozwinięciu wyznacznika otrzymamy wielomian stopnia N (ze względu na niewiadomą E). Wobec tego, po przyrównaniu wyznacznika do zera, otrzymamy równanie stopnia N. Równanie to będzie miało zatem N pierwiastków (czyli rozwiązań), którymi będzie zbiór wartości E, czyli E₁, E₂, ..., E_N

Energie i współczynniki (uzyskiwane z układu równań wiekowych)

Po rozwiązaniu równania i uzyskaniu jednej z wartości E, np. E_i ,

możemy wstawić pierwiastek E_i do układu równań wiekowych, czyli do
, a następnie znaleźć współczynniki c_q odpowiadające danej wartości energii E_i. Ponieważ dla każdej energii otrzymamy inny zestaw współczynników c_q, wprowadzimy dodatkowy indeks (aby je rozróżniać), oznaczając przez c_iq (i=1,2, ..., N). Czyli np. po uzyskaniu energii E₁ możemy z kolei uzyskać współczynniki c₁₁, c₁₂, c₁₃, ..., c_1N, odpowiadające tej energii natomiast po uzyskaniu energii E₂ możemy z kolei uzyskać współczynniki c₂₁, c₂₂, c₂₃, ..., c_2N, odpowiadające energii E₂.

Energia i funkcja falowa stanu podstawowego (uzyskiwane z układu równań wiekowych)

Jeżeli E_i jest najmniejszym pierwiastkiem równania uzyskanego przez przyrównanie wyznacznika wiekowego do zera, to wartość ta odpowiada (przybliżonej) energii stanu podstawowego badanego układu, a odpowiednie współczynniki c_i1, c_i2, c_i3, ..., c_iN określają (przybliżoną) funkcję falową dla stanu podstawowego, czyli:

φ_i = c_i1 χ₁ + c_i2 χ₂ + c_i3 χ₃ + ...+ c_iN χ_N

czyli w skróconym zapisie:

96

---