Ćwiczenie nr 13

1) Cel ćwiczenia

Wyznaczenie parametrów drgań układu.

2) Podstawy teoretyczne.

Rozpatrujemy drgania układu mechanicznego przedstawionego na rysunku poniżej.

Układ ten składa się z bębnów obracających się w przeciwne strony.

L

Przy wyprowadzeniu równania ruchu pręta korzystamy z zasady d'Alamberta zapisaną w postaci wektorowej:

-m

Dla danego układu :

• m
  

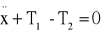
Za stan równowagi uważamy takie położenie środka masy, kiedy zachodzi N₁ = N₂ , a więc leży on w połowie odległości pomiędzy osiami bębnów. Po wysunięciu środka masy pręta o wielkość x z położenia równowagi otrzymamy:

N₁ =

Siły tarcia będą równe:

T₁ = μ N₁ = μmg

- m
μmg
- równanie ruchu pręta

Dokonując podstawienia : ω² = μ
otrzymujemy
= 0 (1)

Jest to równanie opisujące drgania swobodne bez tłumienia o jednym stopniu swobody.

x = C₁sinωt + C₂cosωt - rozwiązanie równania (1) w postaci trygonometrycznej.

3. Opracowanie wyników

Materiał pręta	L (m)	Wielkości dane		Wielkości mierzone			Wielkości obliczone			Uwagi
				Xo (m)	n Obr/min.	T1 (S)	T2 (S)	T3 (S)	Tśr (S)		ω (1/s)	μ (-)
		Drewno	1,2	0,2	90	4,9	4,9	5,0	4,93	1,27
				0,13	60	4,5	4,6	4,6	4,57	1,37
				0.14	70	4,9	4,8	4,8	4,83	1,3
		Mosiądz	1,64	0,3	160	5,1	5,1	5,1	5,10	1,23
				0,18	120	5,2	5,1	5,2	5,17	1,21
				0,15	80	5,2	5,1	5,2	5,17	1,21

Wnioski :

Obliczony współczynnik tarcia pręta drewnianego po rolkach metalowych, nieznacznie odbiega wartością od podanego w literaturze ( „Tablice matematyczne, fizyczne, chemiczne i astronomiczne ). Taka różnica wartości mogła być spowodowana zbyt małą ilością kredy na rolkach lub tym, że pręt drewniany miał gładką powierzchnię spowodowaną długotrwałym używaniem.

Wyznaczony współczynnik pręta mosiężnego po rolkach metalowych jest także zbliżony do wartości literaturowej, tzn. pomiar był przeprowadzony dokładnie.

---