Wydział Elektroniki Politechniki Wrocławskiej	Laboratorium miernictwa elektronicznego
^Wykonali		^Grupa 6	^Ćw. nr 4	^Prowadzący mgr R. Szczepanowski
Kompensacyjna metoda pomiaru napięcia i jej zastosowanie w kompensacyjnym przetworniku A/C		^Data wykonan^ia 98.04.28	^Data oddania 98.05.05	^Ocena

CEL ĆWICZENIA:

Celem ćwiczenia jest poznanie zasady pomiaru oraz źródeł błędów w pomiarze napięcia metodą bezpośredniego porównania z wzorcem oraz sposobu technicznej realizacji tej zasady i zwrócenie uwagi, że zautomatyzowanie pomiaru tą metodą doprowadziło do powstania kompensacyjnych przetworników A/C.

WYKAZ PRZYRZĄDÓW :

1. Źródło napięcia wzorcowego ZB-1

[V]

E_W = ± 0,2%E_W ± 10 mV

R_W = 100 

Ziarno regulacji wzorca: 0,01 V

2. Źródło napięcia wzorcowego ZD-1

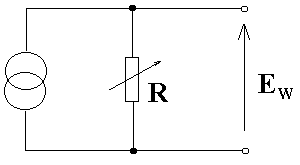
E_W = R⋅10 mA

I = 10 mA ± 0,05%

×1 - kl. 0,1

Klasa R: ×10 - kl. 0,05

×100 - kl. 0,05

3. Źródło napięcia wzorcowego ZD-2

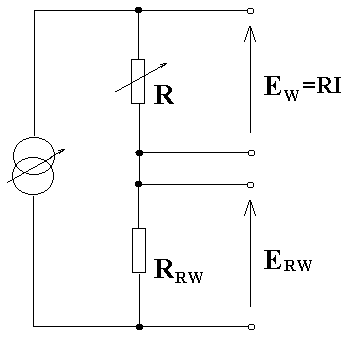
R_RW = 101,87 

E_RW = 101,87⋅I

stabilność prądu 0,005%

×0,1 - kl. 0,5

Klasa R: ×1 - kl. 0,1

×100, ×10 - kl. 0,05

4. Źródło Ex-1

E_wyj = E_x [V] ± 10%

R_W ≤ 200 

5. Komparator napięć KN-1

_max = 20 dz

R_RW = 2000  dla C_i = 500 A/dz

R_RW = 500  dla C_i = 50 A/dz

R_RW = 250  dla C_i = 5 A/dz

6. Komparator dwustanowy SFC-2211

7. Ogniwo normalne E_N200 = (1,0187 ± 0,0002) V, R_W ≤ 600 

PRZEBIEG ĆWICZENIA :

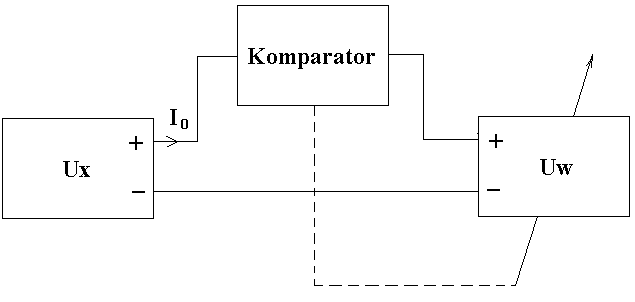
1. Pomiar Ex metodą kompensacji z zastosowaniem źródła ZB-1

a) komparator jednostanowy

Ew	Ex	Ci		Ex	Ex ± Ex
[ V ]	[ V ]	[ A/dz ]	[ dz ]	[ V ]	[ V ]
0,01(2^0+2^1+2^2+2^5+2^6) = 1,03	1,03	5	1	0,02	1,03 ± 0,02
0,01(2^1+2^2+2^3+2^6+2^7) = 2,06	2,06	5	1	0,03	2,06 ± 0,03

Ex = Ew

Ex = Ex ± (Ew + Ez)

Ez = (Er ∪ Ep) + Ee - błąd zrównania

Ep = I₀R_k = C_iR_k- czułość komparatora

Ee = I₀(R_x + R_N) = C_i(R_x + R_N) - błąd wynikający z poboru mocy

Er - ziarno regulacji wzorca

gdzie: R_k - rezystancja wewnętrzna komparatora

R_x - rezystancja wewnętrzna mierzonego źródła napięcia

R_N - rezystancja wewnętrzna wzorcowego źródła napięcia

Przykładowe obliczenia:

Ep = 5⋅10^-6⋅1⋅250 = 1,25 mV

Er = 10 mV

Ee = 5⋅10^-6⋅1⋅(200+100) = 1,5 mV

Ez = 10+1,25+1,5 = 12,75 mV

Ew = 0,2%⋅1,03+10 = 12,06 mV

Ex = Ez + Ew = 0,02 V

b) komparator dwustanowy

Ew < Ex dla Ew [V]	Ew ≥ Ex dla Ew [V]
1,03 (n=6,5,2,1,0)	1,04 (n=6,5,3)
2,06 (n=7,6,3,2,1)	2,07 (n=7,6,3,2,1,0)

Szukaliśmy takich wartości napięcia, które różnią się co do wartości ziarnem regulacji wzorca, a komparator zmienia stan, dlatego wartość mierzona zawiera się w przedziale:

Ex ∈ [Ew₁±Ew₁, Ew₁±Ew₁]

Ex₁ ∈ [1,03±0,01 ; 1,04±0,01]

Ex₂ ∈ [2,06±0,01 ; 2,07±0,01]

Wartości błędów Ew wyliczane są w identyczny sposób jak w punkcie poprzednim ze wzoru

E_W = ± 0,2%E_W ± 10 mV

2. Pomiar Ex metodą kompensacji z zastosowaniem źródła ZD-1

Ew	Ex	Ci		Ex	Ex ± Ex
[ V ]	[ V ]	[ A/dz ]	[ dz ]	[ V ]	[ V ]
0,01(100+3) = 1,03	1,03	5	0	0,002	1,03 ± 0,01
0,01(200+6) = 2,06	2,06	5	0,5	0,01	2,06 ± 0,01

Ex = Ew

Ex = Ex ± (Ew + Ez)

Ez = (Er ∪ Ep) + Ee - błąd zrównania

Ep = I₀R_k = C_iR_k- czułość komparatora

Ee = I₀(R_x + R_N) = C_i(R_x + R_N) - błąd wynikający z poboru mocy

Er - ziarno regulacji wzorca

gdzie: R_k - rezystancja wewnętrzna komparatora

R_x - rezystancja wewnętrzna mierzonego źródła napięcia

R_N - rezystancja wewnętrzna wzorcowego źródła napięcia

R = δR⋅R

δEw = δR + δI

Ew = (δR + δI)Ew

Przykładowe obliczenia:

Ep = 5⋅10^-6⋅0,5⋅250 = 0,6 mV

Er = 10mA⋅1 = 10 mV

Ee = 5⋅10^-6⋅0,5⋅(200+206) = 1 mV

Ez = 10+1,25+1,5 = 11,6 mV

R = 200⋅0,05%+6⋅0,1% = 0,106 

I = 0,05%⋅10 = 0,005 mA

Ew = (0,05% + 0,05%)2,06 = 2,06 mV

Ex = Ez + Ew = 0,01 V

3. Pomiar Ex metodą kompensacji z zastosowaniem źródła ZD-2 (kompensacja podwójna)

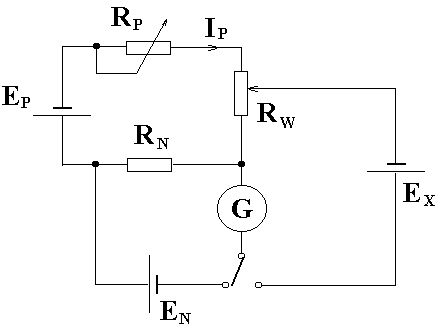
R_p = 101,87 

R_N = 600 

E_N = 1,0187 V

Dla bezpieczeństwa galwanometru w układzie przedstawionym na rys. obok zastosowano tłumik.

Wyniki pomiarów:

R_W = 153,7  Ex = 1,0187⋅153,7/600 = 0,261 V

R_W = 64,2  Ex = 1,0187⋅64,2/600 = 0,109 V

R_W = 11,1  Ex = 1,0187⋅11,2/600 = 0,019 V

Błąd pomiaru (metoda różniczki zupełnej):

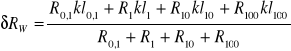
R_w = δR⋅R_w

WNIOSKI I UWAGI:

W pkt.1 i 2 ćwiczenia mierzyliśmy napięcia metodą kompensacyjną. Na błąd pomiaru składają się takie czynniki jak błąd zrównania, czułości komparatora, poboru mocy, źródła wzorcowego, ziarno regulacji wzorca. Analizując błędy na podstawie pomiarów można stwierdzić, że w naszym przypadku największym czynnikiem błędu sumarycznego jest ziarno regulacji wzorca.

Porównując wyniki pomiaru dla komparatora jednostanowego i dwustanowego widzimy, że dokładniejszy przedział wartości błędu możemy wyznaczyć dla komparatora dwustanowego. W naszym przypadki wynosi on Ex =0,01 V. Błąd ten zależy od błędu wartości wzorcowej, ziarna regulacji wzorca oraz czułości komparatora.

W ćwiczeniu można było wykorzystać dwie metody kompensacji: schodkową i wagową. Kompensacja schodkowa jest szybsza dla małych wartości napięcia, zaś dla większych napięć szybsza jest kompensacja wagowa.

W pkt. 3 ćwiczenia mierzyliśmy napięcia metodą kompensacji podwójnej. Aby nie uszkodzić galwanometru do układu dołączono tłumik. Wartości napięcia uzyskane tą metodą są teoretycznie dokładniejsze, dlatego układy takie wykorzystuje się w przetwornikach A/C. Uzyskane przez nas wyniki pomiarów są ok. 5 razy mniejsze od oczekiwanych. Spowodowane jest to wadliwą pracą tłumika (w pomiarach służył on jako separator). Błąd pomiaru opracowano metodą różniczki zupełnej, lecz nie wyliczano wartości liczbowych ze względu na w/w przyczynę.

________________________________________________________________________________

Porównanie napięć komparatorem dwustanowym:

Ex = Ew, gdzie Ew jest napięciem, przy którym komparator zmienia stan

Błędem jest ziarno regulacji wzorca

(Za Ew przyjmuje się jedno z napięć, np. w naszym przypadku 1,03 lub 1,04V, a błąd pomiaru to 10mV)

---