Łączenie ogniw

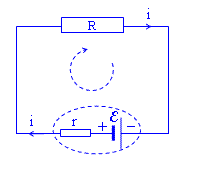
"Oczko". 
Z prawa Ohma dla obwodu zamkniętego mamy:

Otrzymaliśmy drugie prawo Kirchhoffa. Pozwala ono na szybkie rozwiązywanie obwodów z ogniwami. Jeśli z obwodu wyodrębnimy dowolną zamkniętą pętle ("oczko"), to wychodząc z jakiegoś jej miejsca, będziemy napotykali wzrosty potencjałów (dodatnie napięcia), spadki potencjałów (ujemne napięcia) oraz siły elektromotoryczne. Wartości SEM będziemy uważać za dodatnie, gdy będziemy szli przez ogniwo od jego minusa do plusa i za ujemne, gdy będziemy szli od plusa do minusa. Po przejściu całego oczka suma SEM i spadków potencjałów musi być równa zero - wrócimy do tego samego miejsca, czyli do tego samego potencjału.
Zastosujmy ten tok myślenia do obwodu wyżej idąc po oczku zgodnie ze strzałką. Przez ogniwo idziemy od minusa do plusa, zatem mamy 
. Idąc przez opór rporuszamy się zgodnie z kierunkiem przepływu prądu, a ten płynie od potencjału wyższego do niższego. Napięcie na oporze wewnętrznym jest -ir. Przez opór zewnętrzny R też idziemy zgodnie z kierunkiem prądu, czyli od potencjału wyższego do niższego. Napięcie na tym oporze jest -iR. Dodając SEM i różnice potencjałów mamy: 
 - ir - iR = 0, czyli drugie prawo Kirchhoffa. Tak będziemy postępowali również w przypadku obwodów bardziej złożonych.

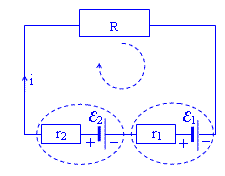
Szeregowe łączenie ogniw. 
Przez oba ogniwa i opór zewnętrzny R płynie ten sam prąd i (rysunek obok). Dla oczka, z którym mamy do czynienia, piszemy:
₁ - ir₁ +  
₂ - ir₂ - iR = 0. Prąd, który płynie w obwodzie jest:

W praktyce nzjczęściej mamy do czynienia z sytuacją, w której dysponujemy pewną ilością (n) identycznych baterii. Wtedy:

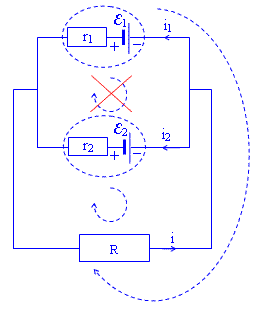
Równoległe łączenie ogniw. 
Piszemy I prawo Kirchhoffa dla całego obwodu, II prawo Kirchoffa dla dużego oczka, dla małego i małego przekreślonego:

Czwarte równnie nic nie wnosi, ponieważ otrzymujemy je również przez odjęcie trzeciego od drugiego. Z drugiego i trzeciego równania wyznaczamy i₁ oraz i₂ i wstawiamy do pierwszego otrzymując:

Gdy mamy n identycznych ogniw, wtedy:

Jakie wybrać łączenie ogniw? 
Prądy płynące z baterii ogniw połączonych szeregowo i równolegle możemy przedstawić wzorami:

Chcąc otrzymać z baterii jak największy prąd, w pierwszym przypadku wybierzemy połączenie szeregowe, w drugim równoległe.

---