BADANIA OPERACYJNE (wykład) Elżbieta Sobczak

6-10-2001

1. Stanisław Krawczyk „Badania operacyjne dla menedżerów” AE Wrocław;

2. „Badania operacyjne w przykładach i zadaniach” PWN pod red. Karola Kukuły.

Testy z teorii, na drugiej kartce zadania i razem dwie oceny

Badania operacyjne należą do zespołu nauk o zarządzaniu i organizacji. Nauka samodzielna, ma własny przedmiot badań, własne metody badawcze i cechująca się charakteryzującym podejściem do badanych zjawisk.

Badania operacyjne- zbiór naukowych metod zarządzania zastępujących metody intuicyjne w złożonych warunkach występowania sytuacji decyzyjnych. Na podstawie odpowiednio zgromadzonych danych umożliwiają podejmowanie decyzji optymalnych.

Wybór jest najczęściej wspomagany komputerowo.

Przedmiot BO to decyzje kierownicze o różnym zasięgu oddziaływania mające charakter strategiczny, taktyczny lub operacyjny.

Metody badawcze- matematyczne, heurystyczne i symulacyjne.

Cechy charakterystyczne:

₁. ukierunkowanie na podejmowanie decyzji;

₂. podejście systemowe (całościowe);

₃. interdyscyplinarny charakter badań operacyjnych;

₄. podejmowanie decyzji na podstawie modeli decyzyjnych analizowanych systemów;

₅. występująca konieczność stosowania techniki komputerowej.

FAZY BADAŃ OPERACYJNYCH

1. ETAP I DIAGNOZA PROBLEMU

- postrzeganie problemu;

FAZA - predykcja stanów otoczenia;

DIAGNOZY - określanie kryteriów wariantów decyzyjnych;

- analiza danych historycznych i bieżących.

2. FORMUŁOWANIE PROBLEMU

- precyzyjne określenie celu działania;

- określenie czynników od których zależy osiągnięcie celu;

3. BUDOWA MODELU

FAZA - opracowanie modelu konceptualnego;

MO- - opracowanie modelu komputerowego;

DE- IV. ANALIZA MODELU

LOWA- - generowanie i analiza wariantów decyzyjnych;

NIA - wybór i opracowanie decyzji ostatecznej;

- eksperymentowanie na modelu decyzyjnym (symulacja).

V. WDRAŻANIE WYNIKÓW

FAZA - dobór środków do realizacji decyzji;

WDRA- - kontrola realizacji;

ŻANIA - wyniki wdrożenia.

WYNIKÓW

ANALIZA PROBLEMU DECYZYJNEGO- ogół działań w wyniku których następuje podjęcie decyzji (rozwiązanie problemu).

Proces decyzyjny polega na opracowaniu i analizie wariantów decyzyjnych oraz na wyborze spośród nich wariantu najlepszego.

DECYZJA- akt wyboru jednego wariantu, działanie spośród wielu możliwych.

PROCES DECYZYJNY składa się z elementów:

1. decydent (podmiot podejmowania decyzji)

2. zbiór wariantów decyzyjnych (możliwych rozwiązań modelu)

3. funkcja decyzyjna in. funkcja kryterium lub celu- to zasada wskazywania rozwiązania spośród różnych wariantów decyzyjnych

4. informacja o stanach otoczenia

5. inne elem. zależne od konkretnej sytuacji decyzyjnej.

ETAPY PROCESU DECYZYJNEGO:

1. sformułowanie problemu i określenie celu decyzji

2. zebranie inf. niezbędnych do podjęcia decyzji (kompletność, selektywność, wiarygodność)

• inf. o stanie obiektu gospodarczego,

• inf. o celach wytyczonych przez decydenta,

• inf. o koniecznych działaniach.

3. ustalenie możliwych wariantów decyzyjnych (zależy od złożoności obiektu, liczby inf., horyzontu czasowego, podejmowanej decyzji i zasięgu decyzji)

WARUNKI OGRANICZAJĄCE- warunki określające jakie decyzje mogą być podjęte. Czynniki zewnętrzne nie zależne od decydenta.

DECYZJE DOPUSZCZALNE- decyzje uwzględniające warunki ograniczające.

POLE DECYZYJNE- zbiór decyzji dopuszczalnych.

4. wybór optymalnego wariantu decyzji (funkcja decyzyjna jest kryterium optymalności

DECYZJA OPTYMALNA- decyzja dopuszczalna, realizująca postawiony cel w sposób możliwie najlepszy.

5. sformułowanie decyzji i jej wprowadzenie w życie

Decyzja musi mieć: wykonawcę, terminy realizacji, metody wykonania decyzji, formy przekazu, określone rodzaje motywacji i sposoby motywowania.

6. kontrola wykonania decyzji

Jej cel- sygnalizacja różnic m. stanem rzeczywistym a stanem pla-nowanych różnic i ewentualna korekta decyzji przed jej całkowitą realizacją jeśli nie prowadzi do osiągnięcia założonego celu.

Warunki w jakich może być podejmowana decyzja ze względu na stopień niepewności otoczenia zew.

1. warunki pewności- jest podejmowana, jeśli można uważać, że w trakcie realizacji decyzji środowisko nie wpłynie w żaden istotny sposób na wartość charakterystyk decyzji;

2. warunki niepewności- jest podejmowana jeśli wartości charakterystyk decyzji zależą od stanu środowiska ale nie można określić prawdopodobieństwa wystąpienia poszczególnych stanów środowiska;

3. warunki ryzyka- jest podejmowana jeżeli środowisko może wpłynąć na wartości charakterystyk decyzji i znane są prawdopodobieństwa występowania poszczególnych stanów otoczenia.

Ad 1.

x₁ y₁

x₂ y₂

Ad 2.

y₁

x₁ y₂

y₃

Ad 3.

y₁ p₁

x₁ y₂ p₂

y₃ p₃

Sposoby podejmowania decyzji w warunkach pewności:

1. bezpośrednie porównywanie wartości charakterystyk dla każdego wariantu decyzyjnego

2. kryterium Borda

3. wykorzystanie systemu premiowania

Ad b) etap I- przypisanie każdemu wariantowi punktów za miejsce ze względu na wartość danej charakterystyki

(n-wariantów decyzyjnych i wtedy najkorzystniejsza alternatywa wykorzystuje n-punktów a najmniej n-1 punkt;

etap II- sumowanie punktów jakie uzyskała każda alternatywa ze względu na wartości poszczególnych charakterystyk;

etap III- wybór alternatywy optymalnej, jest nią ta która uzyskała maksymalna liczbę punktów.

Cechy charakterystyczne kryterium Borda: wykorzystuje minimalną ilość inf. wyłącznie o charakterze porządkowym; kryterium to nie wykorzystuje inf. o uporządkowaniu celu wg ich wartości, kryterium to nie zawsze w sposób jednoznaczny wskazuje decyzję; prostota, odręczny sposób sprawdzenia decyzji.

Ad c) wszystkie cele przed przystąpieniem do realizacji muszą być uporządkowane wg ważności (najważniejszy itd.)

System premiowania

Cele zostały uporządkowane wg ich ważności, i-ty jest ważniejszy od i+1.

Tworzy się system premii i przedstawia w postaci macierzy P

P = [ p_ir ] _(kxn)

i = 1,..., k (numer celu)

r = 1,..., n (numer miejsca)

p_ir - premia przyznawana za zajęcie r-tego miejsca w osiągnięciu i-tego celu.

ZASADY USTALANIA PREMII:

1. im dalsze miejsce w osiągnięciu danego celu tym mniejsza (lub nie większa) powinna być premia

p_ir ≥ p_i,r+1

2. im więcej ważny cel tym mniejsza (lub nie większa) powinna być premia za to samo miejsce

p_ir ≥ p_i+1,r

Etapy tej teorii:

1. utworzenie systemu premiowania;

2. uporządkowanie premii od największej do najmniejszej i zapisanie ich w ciągu;

3. przypisanie każdej premii numeru zajmowanego przez nią miejsca, jeżeli występują jednakowe premie otrzymują numer będący średnią arytmetyczną z numerów jakie wynikają z kolejności ciągów (np. 1; 2; 3; 3,5; 4);

4. uporządkowanie alternatyw ze względu na wartości poszczególnych charakterystyk;

5. przypisanie alternatywom premii i obliczenie dla każdej z nich globalnego wskaźnika miejsca

(Aj) = r_ij

r_ij - numer miejsca przyporządkowany alternatywie Aj ze względu na osiągnięcie i-tego celu

6. wybór alternatywy optymalnej

(Aj) → min

20.10.2001 (w)

Podejmowanie decyzji w warunkach niepewności.

Są to wyniki trudne, jest zbyt mało informacji.

Sytuacje decyzyjne:

1. w kt. można określić alternatywy, warianty decyzyjne;

2. wyniki działań zależą w sposób istotny od wpływu środowiska, kt. jest poza kontrolą decydenta;

3. można wyróżnić charakterystyczne stany środowiska;

4. znane są konsekwencje wystąpienia poszczególnych stanów środowiska.

Podstawy formalne podejmowania decyzji w warunkach niepewności:

1. określone pole decyzyjne- jako zbiór decyzji dopuszczalnych zwanych alternatywami

D = {A_j} = {A₁, A₂,..., A_n}

i = 1,..., n - numer alternatywy;

2. określono charakterystykę C. Problem decyzyjny przedstawiono za pomocą celu reprezentowanego przez charakterystykę C.

3. Określono warunek kierunkowy W jaki powinna spełniać charakterystyka C aby cel został osiągnięty (C→max lub C→min)

4. Określono zbiór stanów środowiska

S = {S_j} = {S₁, S₂,...,S_m}

j = 1,..., m- numer stanu środowiska

5. Określono przyporządkowanie

(A_i, S_j) → k_ij

i = 1,...,n- numer alternatywy,

j = 1,...,m- numer stanu środowiska,

k_ij- wartość charakterystyki C dla i-tej alternatywy i j-tego stanu środowiska;

wektor konwencji A_i = (k_i1, k_i2,..., k_im)_{(1 x m.)}

6. Pole decyzyjne przedstawiono jako macierz konsekwencji

k =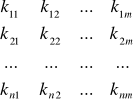

(mn)

i = 1,..., n- numer alternatywy

j = 1,..., m.- numer stanu środowiska

Porządkowanie alternatyw w warunkach niepewności-

Polega na identyfikacji alternatyw zdominowanych i wyeliminowaniu ich z pola decyzyjnego.

Alternatywa zdominowana- mniej korzystna od innej;

Alternatywa dominująca- jednoznacznie korzystniejsza od innej.

Alternatywy są sprawne wtedy gdy żadna nie jest korzystniejsza od drugiej.

W warunkach niepewności przy podejmowaniu decyzji może wystąpić:

1. dominacja absolutna

2. dominacja stanowa

ad 1) alternatywa A_i dominuje w sposób absolutny nad altern. A_p jeżeli najmniej korzystny wynik dla A_i jest nie gorszy dla najkorzystniejszego wyniku dla A_p.

Np. C→zysk przedsiębiorstwa; W:C→max

	S1	S2	S3
A1	30	40	60
A2	20	50	60
A3	10	15	25

A₁ nie dominuje w sposób absolutny A₂

A₁ dominuje w sposób absolutny nad A₃

Ad 2) alternatywa A_i dominuje w każdym stanie otoczenia nad altern. A_p jeżeli w każdym stanie A_i jest nie gorsza niż A_p i istnieje taki stan w kt. A_i jest korzystniejsza od alternatywy A_p.

	S1	S2	S3
A1	30	20	15
A2	30	25	10
A3	25	17	15

C→koszt przedsiębiorstwa; W:C→min

A₃ dominuje w sposób stanowy nad A₁, A₁ zostaje wyeliminowane.

Metody podejmowania decyzji w warunkach niepewności (związane z teorią gier „gry człowieka z naturą”)

1. Reguła Walda (reguła max-min-max lub min-max-min) reprezentuje postawę pesymistyczną;

Algorytm:

1. dla każdej alternatywy należy wskazać wynik najgorszy;

2. należy wskazać alternatywę dla kt. wynik jest najkorzystniejszy;

Reguła Walda przyjmuje więc postać:

1. max min (k_ij); dla W:C→max

i j

2. min max (k_ij); dla W:C→min

i j

2. Reguła max-max lub min-min, skrajnego optymisty, ryzykancka;

Algorytm:

1. dla każdej alternatywy wskazuje się wynik najkorzystniejszy;

2. wybiera się alternatywę dla kt. wynik był najlepszy;

1. max max (k_ij); dla W:C→max

i j

2. min min (k_ij); dla W:C→min

i j

3. Reguła Hurwicza, repr. postawę pośrednią decydenta, wykorzystuje się w niej średnią warzoną skrajnych wyników;

Algorytm:

1. należy subiektywnie ustalić wartość współczyn. optymizmu λ

λ
<0,1>

np. 0,7→ w 70% jest szansa że zajdą najkorzystniejsze okoliczności;

1 - λ → współczynnik pesymizmu;

2. dla każdej alternatywy należy obliczyć wartość funkcji:

• 
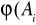
  ) = max (k_ij) + (1-λ) min (k_ij); jeżeli W:C→max

j j

• 
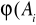
  ) = min (k_ij) + (1-λ) max (k_ij); jeżeli W:C→min

j j

3. należy wybrać tę alternatywę dla kt. średnia warzona wyników jest najkorzystniejsza (maksymalna przy maksymalizacji, minimalna przy minimalizacji);

Jeżeli λ = 0→ to ta reguła będzie przypisana regule Walda;

Jeżeli λ = 0→ to otrzymamy regułę skrajnie optymistyczną (max-max, min-min)

4. Reguła Laplace'a, średniej konsekwencji lub średniej wyników;

Algorytm:

1. dla każdej alternatywy należy obliczyć średnią wyników (konsekwencji)

k_i = 1/m

2. należy wybrać tę alternatywę dla kt. ta średnia jest najkorzystniejsza.

5. Reguła Niehansa-Savage'a, reguła minimalizacji utraconej szansy; wybiera ten kt. chce zminimalizować skutki błędnej decyzji

Algorytm:

1. na podstawie macierzy konsekwencji dla każdego stanu środowiska należy ustalić najkorzystniejszy wynik, będzie to:

1. max (k_pj); dla W:C→max

p

2. min (k_pj); dla W:C→min

p

2. należy utworzyć macierz strat alternatywnych będących konsekwencjami błędnych decyzji:

1. u_ij = max (k_pj) - k_ij; jeżeli W:C→max

p

2. u_ij = k_ij - min (k_pj); jeżeli W:C→min

p

u_ij- element macierzy strat alternatywnych; strata wynikająca ze wskazania i-tej alternatywy jeżeli wystąpi j-ty stan środowiska;

3. dla każdej alternatywy należy obliczyć największą potencjalną stratę

ϕ (A_i) = max (u_ij)

j

4. należy wskazać tą alternatywę dla kt. strata jest najmniejsza

ϕ (A_p) = min ϕ (A_i)

i

Podejmowanie decyzji w warunkach ryzyka

Wszystkie podstawy podejmowania decyzji są analogiczne jak w warunkach niepewności z tym że wprowadza się jeszcze jedno założenie:

• określone są prawdopodobieństwa P_j poszczególnych stanów środowiska i spełniają one relacje:

Najczęściej stosowana reguła: Reguła Bayesa (wartości oczekiwanej):

1. dla każdej alternatywy A_i należy obliczyć wartość oczekiwaną wyników

ϕ (A_i) = μ_i =

μ_i- wartość oczekiwana wyników i-tej alternatywy,

p_j- prawdopodobieństwo wystąpienia j-tego stanu środowiska.

2. Należy wskazać tę alternatywę dla kt. wartość oczekiwana wyników jest najkorzystniejsza (regułę tę można stos. dla decyzji wielokrotnie powtarzalnych).

Szukasz gotowej pracy ?

To pewna droga do poważnych kłopotów.

Plagiat jest przestępstwem !

Nie ryzykuj ! Nie warto !

Powierz swoje sprawy profesjonalistom.

2

Szukasz gotowej pracy ?

To pewna droga do poważnych kłopotów.

Plagiat jest przestępstwem !

Nie ryzykuj ! Nie warto !

Powierz swoje sprawy profesjonalistom.

T

T

T

---