POLITECHNIKA ŚLĄSKA

W GLIWICACH

WYDZIAŁ MECHANICZNY TECHNOLOGICZNY

AUTOMATYKA I ROBOTYKA

LABORATORIUM Z FIZYKI

Ćwiczenie nr 9

Temat: Pomiar pojemności i indukcyjności

Grupa 3

Sekcja 6

15 kwietnia 1996 r.

Michał PATALONG

Marcin SOBOLEWSKI

WPROWADZENIE

Pojemność elektryczna jest zdolnością do gromadzenia ładunków i mierzona jest stosunkiem ładunku do dodatkowego potencjału wytworzonego przez ten ładunek:

Jednostką pojemności jest farad (, , , ). Pojemność kondensatora zależy od jego konstrukcji i wyrażona jest poprzez napięcie między okładkami:

Indukcyjność (indukcyjność własna) charakteryzuje obwód elektryczny wytwarzający skojarzony strumień magnetyczny indukcji i zwykle definiowana jest jako siła elektromotoryczna indukcji wywołana jednostkową szybkością zmiany prądu elektrycznego

W układzie SI jednostką indukcyjności jest henr. Indukcyjność zależy od wymiarów i konfiguracji przestrzennej elementu obwodu oraz od przenikalności magnetycznej ośrodka otaczającego ten przewodnik, np. dla długiego solenoidu:

gdzie N - liczba zwojów, S - przekrój poprzeczny obwodu magnetycznego, l - długość cewki.

Praca zmiennego prądu elektrycznego w czasie jednego okresu płynącego przez opornik R wynosi:

Dla prądu stałego wynosi:

Prąd I_sk , który wykonałby taką samą pracę w tym samym czasie wynosi:

I_sk nazywa się wielkością skuteczną natężenia prądu.

W obwodzie, w którym połączone są szeregowo opornik R i cewka o indukcyjności L zasilanym zmiennym prądem opór indukcyjny wynosi:

W obwodzie tym prąd jest opóźniony w fazie względem napięcia.

W obwodzie, w którym połączone są szeregowo opornik R z kondensatorem o pojemności C zasilanym zmiennym prądem opór pojemnościowy wyraża się wzorem:

W tym układzie prąd wyprzedza napięcie.

W układzie prądu zmiennego zawierającego zarówno cewkę o indukcyjności L, jak i kondensator o pojemności C, a także opór R popłynie prąd elektryczny:

gdzie zawada (opór pozorny):

Natężenie prądu zmiennego, zgodnie z nazwą, zmienia się w czasie, przy czym najczęściej zmiany te opisane są funkcją harmoniczną:

gdzie - amplituda natężenia prądu (wartość szczytowa), - pulsacja (częstość):

- częstotliwość prądu (np. Dla sieci elektrycznej - 50 Hz), T - okres zmian prądu, - faza początkowa.

Wartość skuteczna natężenia prądu:

W praktyce właśnie te wielkości utożsamiamy z natężeniem lub napięciem prądu zmiennego. Np. dla sieci elektrycznej napięcie U = 220 V oznacza właśnie wartość skuteczną napięcia, a równanie tego napięcia zapisalibyśmy w postaci:

Mierniki prądu zmiennego mierzą zwykle wartość skuteczną napięcia lub natężenia prądu.

ZESTAWIENIE WIELKOŚCI W OBWODZIE PRĄDU ZMIENNEGO

NAZWA WIELKOŚCI
FIZYCZNA	ELEKTRO­TECHNICZNA	OZNA-CZENIE	WZÓR
opór	rezystancja
opór indukcyjny	reaktancja indukcyjna
opór pojemnościowy	reaktancja pojemnościowa
zawada	impedancja
przewodnictwo rzeczywiste	konduktancja
przewodnictwo indukcyjne	susceptancja indukcyjna
przewodnictwo pojemnościowe	susceptancja pojemnościowa
przewodnictwo	admitancja

PRZEBIEG ĆWICZENIA

Łączymy obwód prądu stałego wg schematu:

1. 
   

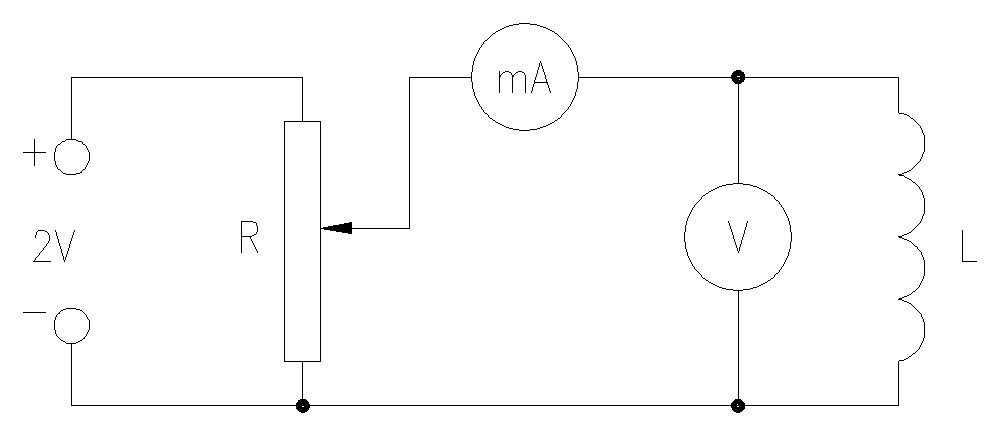
-1. Zmieniając napięcie w granicach 0 * 2 V co 0,2 V notujemy wskazania miliamperomierza.

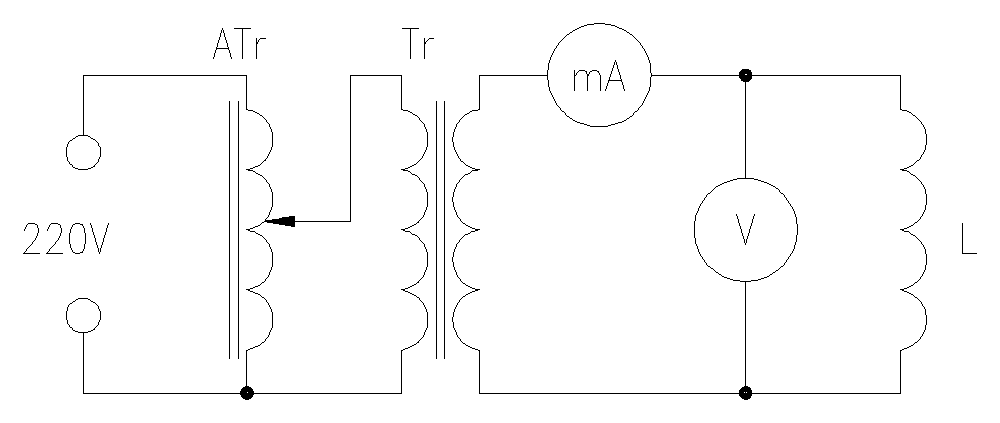
Łączymy obwód prądu zmiennego wg schematu:

3. 
   

Zmieniając napięcie w przedziale 0 * 6 V co 0,5 V notujemy wskazania miliamperomierza. Pomiary wykonujemy dla cewki bez rdzenia i z rdzeniem.

• Łączymy obwód wg schematu:

• 
  

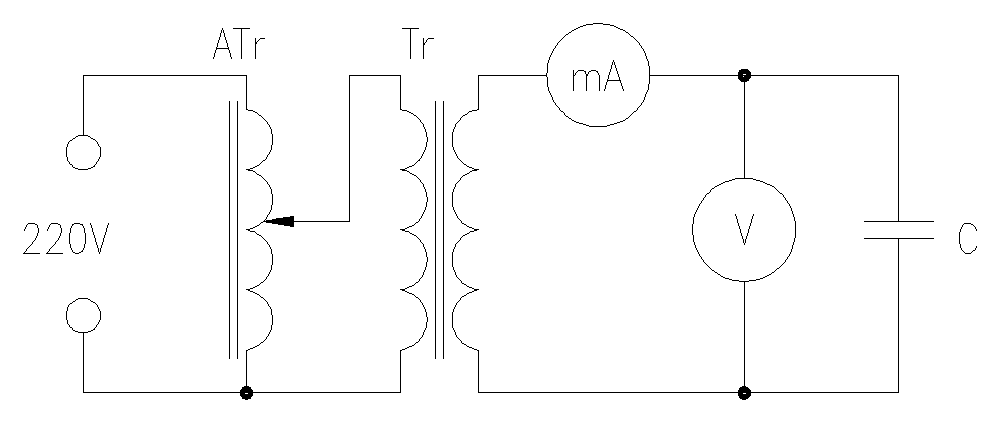
Zmieniając napięcie U w granicach 0 * 6 V co 0,5 V notujemy wskazania miliamperomierza.

Pomiary przeprowadzamy dla 3 kondensatorów oddzielnie oraz połączonych szeregowo i równolegle.

• Nie zapomnij wyłączyć zasilania mierników!

OBLICZENIA

Obliczanie rezystancji cewki

Obliczamy rezystancję cewki na podstawie metody wyrównawczej Gaussa dla wielkości liniowo zależnych. Współczynnik a regresji liniowej ma sens oporu.

gdzie a - współczynnik regresji liniowej:

Po przeprowadzeniu obliczeń otrzymaliśmy następującą wartość:

Błąd wyznaczenia rezystancji obliczamy na podstawie odchylenia standardowego i wynosi on:

ΔR = 25,8 [Ω], wobec tego:

R = (75,2 ± 25,8) [Ω]

Obliczenie impedancji cewki

Impedancję cewki, z rdzeniem jak i bez rdzenia obliczamy tak samo jak rezystancję cewki.. Współczynnik a regresji liniowej ma sens impedancji.

Rachunek błędów przeprowadzamy podobnie.

W wyniku obliczeń otrzymaliśmy następujące wartości:

Impedancja cewki bez rdzenia : Z_b = (148,6 ± 48,2) [Ω],

Impedancja cewki z rdzeniem : Z_r = (667,1 ± 98,4) [Ω].

Obliczenie indukcyjności cewki

Na podstawie wzoru:

obliczamy indukcyjność cewki z rdzeniem i bez rdzenia.

Przeprowadzamy rachunek błędów metodą różniczki zupełnej.

czyli:

Po wstawieniu wartości otrzymano:

ΔLb = 5,698•10^-5 [H] - Błąd pomiaru indukcyjności cewki bez rdzenia,

ΔLr = 4,274•10^-4 [H] - Błąd pomiaru indukcyjności cewki z rdzeniem

Po podstawieniu danych uzyskaliśmy wartości:

Indukcyjność cewki bez rdzenia L = (40700 ± 5,698)•10^-5 [H]

Indukcyjność cewki z rdzeniem L = (21090 ± 4,274) •10^-4 [H]

Obliczenie pojemności kondensatorów

Obliczamy reaktancję kondensatorów na podstawie metody wyrównawczej Gaussa dla wielkości liniowo zależnych. Współczynnik a regresji liniowej odpowiada wartości reaktancji kondensatorów. Błąd wyznaczenia reaktancji obliczamy na podstawie odchylenia standardowego.

Xc1 = (54,5 ± 17,24) kΩ - Reaktancja pojemnościowa pierwszego kondensatora

Xc2 = (11,8 ± 3,744) kΩ - Reaktancja pojemnościowa drugiego kondensatora

Xc3 = (2,9 ± 0,922) kΩ - Reaktancja pojemnościowa trzeciego kondensatora

Xcr = (2,3 ± 0,744) kΩ - Reaktancja pojemnościowa połączenia równoległego kondensatorów

Xcsz = (77,4 ± 24,478) kΩ - Reaktancja pojemnościowa połączenia szeregowego kondensatorów

Obliczamy pojemność kondensatorów wg wzoru:

Rachunek błędów przeprowadzamy metodą różniczki zupełnej:

ΔC1 = 0,018 μF - pierwszy kondensator

ΔC2 = 0,004 μF - drugi kondensator

ΔC3 = 0,348 μF - trzeci kondensator

ΔCr = 0,433 μF - połączenie równoległe kondensatorów

ΔCsz = 0,013 μF - połączenie szeregowe kondensatorów

Otrzymaliśmy wyniki:

C1 = (0,058 ± 0,018) μF = (58 ± 18) nF

C2 = (0,27 ± 0,004) μF = (270 ± 4) nF

C3 = (1,1 ± 0,348) μF = (1100 ± 348) nF

Cr = (1,36 ± 0,433 ) μF = (1360 ± 433 ) nF

Csz = (0,04 ± 0,013) μF = (40 ± 13) nF

Porównujemy doświadczalne wartości pojemności baterii kondensatorów z odpowiednimi wartościami wynikającymi z praw Kirchhoffa:

dla połączenia szeregowego:

Wartość z prawa Kirchhoffa:

Wartość zmierzona i obliczona:

b) dla połączenia równoległego:

Wartość z prawa Kirchhoffa:

Wartość zmierzona i obliczona:

UWAGI I SPOSTRZEŻENIA

Wszystkie pomiary wykonaliśmy starannie według zaleceń zawartych w instrukcji do ćwiczeń. Błędy pomiarowe spowodowane są niepewnością połączeń elektrycznych (tzn. luźne styki). Obliczeń dokonano za pomocą programów EXCEL 7.0 i MATHCAD 6.0.

---