Nr ćwiczenia: 18 |
Temat ćwiczenia: Badanie rezonansu elektrycznego w obwodzie RLC |
Wydział: FTiMK |
Data: 24.10.2000 |
Zespół nr: 4 |
Imię i nazwisko: Elżbieta Pojnar |
Rok: II |
Ocena: |
Jeżeli do obwodu składającego się z opornika o oporze R, kondensatora o pojemności C i cewki indukcyjnej o indukcyjności L, przyłożymy napięcie harmoniczne zmienne:
![]()
to w obwodzie tym popłynie prąd przemienny:
![]()
gdzie: U - wartość chwilowa napięcia
I - wartość chwilowa prądu
U0 - amplituda napięcia
I0 - amplituda prądu
![]()
- częstość kołowa
f - częstotliwość prądu
φ - przesunięcie fazowe prądu względem napięcia
Natężeniem skutecznym prądu przemiennego ISK nazywamy takie natężenie prądu stałego, który wydziela w tym samym czasie tę samą ilość energii co prąd przemienny. Korzystając z tej definicji możemy obliczyć wartość skuteczną dla prądu przemiennego. Ciepło wydzielane w oporniku R przez prąd przemienny w ciągu jednego okresu T jest równe ciepłu wydzielanemu w tym samym czasie przez prąd stały o natężeniu skutecznym ISK.
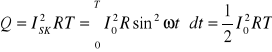
Stąd otrzymujemy:
![]()
Podobnie dla napięcia prądu przemiennego dostaniemy:
![]()
Powyższe dwa wzory możemy zastosować również dla prądu zmiennego. Opór Z obwodu prądu przemiennego nosi nazwę impedancji (zawady) i definiujemy go jako:
![]()
Prąd przemienny ![]()
płynąc przez opór R wywołuje spadek potencjału:
![]()
Nie ma tutaj przesunięcia fazowego między prądem i napięciem, zawada omowa (rezystancja) jest równa R.
Napięcie UL na cewce o indukcyjności L i RL = 0, gdy płynie przez nią prąd przemienny jest równe:
![]()
Napięcie na cewce wyprzedza prąd w fazie o π/2 (lub prąd opóźnia się w fazie względem napięcia o π/2). Zawada indukcyjna XL jest równa
![]()
Podobnie prąd zmienny płynący przez kondensator o pojemności C wywołuje spadek potencjału UC na jego okładkach równy:
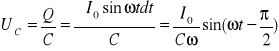
Wówczas napięcie opóźnia się w fazie względem prądu o π/2 (prąd wyprzedza napięcie o π/2). Zawada pojemnościowa XC jest równa:
![]()
Zależność R, XL, XC od częstotliwości prądu zmiennego przedstawiam na wykresie nr2.
W obwodach zawierających R, L, C dla pewnych częstotliwości zmian napięcia zasilania może dojść do zjawiska rezonansu. Jeżeli rozważymy szeregowy obwód RLC napięcia na każdym elemencie obwodu przy przepływie prądu przemiennego wynoszą UR, UL, UC. Natomiast napięcie źródła jest równe:
![]()
Sumowanie napięć możemy wykonać również metodą graficzną. Wykres wektorowy przedstawia rys.3.
Z relacji między napięciami i własnościami trójkąta prostokątnego, który one tworzą otrzymujemy:
![]()
Zatem zawada dana jest wzorem:
![]()
Kąt przesunięcia fazowego prądu względem napięcia obliczamy ze wzoru:
![]()
Przykładając do szeregowego obwodu RLC zmienne napięcie ![]()
otrzymujemy prąd o natężeniu skutecznym:
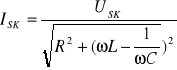
Wzór ten przedstawia równanie krzywej rezonansowej ISK(ω), co ilustruje rys.4.
Rezonans polega na maksymalnym przekazywaniu energii z jednego układu drgającego do drugiego. Zachodzi to wówczas, gdy częstotliwości drgań tych układów są równe. Zjawisko rezonansu występuje nie tylko w obwodach RLC, ale spotykamy także rezonans mechaniczny, akustyczny.
Dla elementów R, L, C największy prąd popłynie wówczas, gdy:
![]()
co odpowiada warunkowi, że XL = XC. Uwzględniając przesunięcie fazowe otrzymamy łączny spadek potencjału na cewce i kondensatorze równy 0. W obwodzie szeregowym RLC występuje wówczas rezonans napięć dla częstości rezonansowej ωr równej częstości drgań własnych układu:
![]()
a prąd rezonansowy Ir przyjmuje wartość:
![]()
gdzie: Ir - skuteczny prąd o maksymalnej wartości. W obwodzie wydziela się maksymalna energia:
![]()
Podobne rozumowanie można przeprowadzić dla równoległego obwodu RLC, gdzie występuje rezonans prądowy. Schemat przedstawia rys.5.
Przy równoległym połączeniu kondensatora i cewki, przesunięcia fazowe prądów są takie, że prądy płyną w gałęziach w przeciwne strony. Jeśli spełniony jest warunek XL = XC, to:
![]()
Wypadkowa oporność Rw równoległego połączenia dąży do nieskończoności. Prąd w nierozgałęzionej części obwodu osiąga wartość minimalną, a prądy płynące w gałęziach zawierających indukcyjność i pojemność wielokrotnie przewyższają prąd źródła. Jest to rezonans prądowy, gdzie zawada jest dana wzorem:
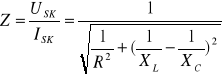
Krzywą rezonansową równoległego obwodu RLC przedstawia rys.6.
Równanie krzywej rezonansowej możemy uzyskać również rozwiązując równanie różniczkowe drgań wymuszonych napięciem ![]()
.
Z drugiego prawa Kirchoffa otrzymamy:
![]()
gdzie:
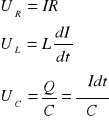
Wstawiając do powyższego równania otrzymamy:
![]()
Po zróżniczkowaniu i przekształceniu równania otrzymamy:
![]()
Jest to równanie różniczkowe drugiego stopnia, które dla ustalonych wartości ma następujące rozwiązanie:
![]()
gdzie:
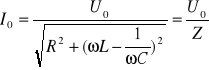
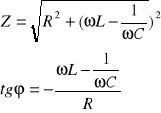
Wyszukiwarka
Podobne podstrony:
18 rezonans, Studia, Semestr 1, Fizyka, Sprawozdania
Lab fiz 43 2, Studia, Semestr 1, Fizyka, Sprawozdania
Lab fiz 15, Studia, Semestr 1, Fizyka, Sprawozdania
Lab fiz 44, Studia, Semestr 1, Fizyka, Sprawozdania
17 - hallotron, Studia, Semestr 1, Fizyka, Sprawozdania
74A, Studia, Semestr 1, Fizyka, Sprawozdania
Ściąga 2 sem, Studia, Semestr 1, Fizyka, Sprawozdania
Zrodlo swiatla za pomoco fotometru, Studia, Semestr 1, Fizyka, Sprawozdania
30, Studia, Semestr 1, Fizyka, Sprawozdania
47, Studia, Semestr 1, Fizyka, Sprawozdania
konspekt f3, Studia, Semestr 1, Fizyka, Sprawozdania
teoretyczna, Studia, Semestr 1, Fizyka, Sprawozdania
sprawozdanie73b, Studia, Semestr 1, Fizyka, Sprawozdania
więcej podobnych podstron