Opracowanie i dyskusja wyników pomiarów

1. Przeliczenie odczytanych wartości h' w mmH₂O na mmHg i na Pa.
   - mmHg
   
   
   
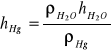
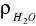
   =1·10³ kg/m³ gęstość wody

=13,6·10³ kg/m³ gęstość rtęci

,
- wysokość słupa wody i rtęci
dla pierwszego punktu pomiarowego : h''=10³·h'/13600=10³·206/13600=15,15 mmHg

- na Pa

760mmHg=1atm=1,013·10⁵ N/m²=1,013·10⁵ Pa

dla pierwszego punktu pomiarowego p'=h''·1,013·10⁵ /760=15,15·1,013·10⁵/760=2018,9Pa
resztę wyników ponizej umieściłam w tabeli.

Nadciśnienie	h'	h"	p'	p=b+p'	τ	T
nr pomiaru	[mmH20]	[mmHg]	[Pa]	[Pa]	[K]	[K]
1	206	15,15	2018,9	103019	4,62	373,15
2	193,5	14,23	1896,4	102896	4,59	373,12
3	175	12,87	1715,1	102715	4,55	373,08
4	158	11,62	1548,5	102549	4,51	373,04
5	143	10,51	1401,5	102401	4,46	372,99
6	119	8,75	1166,3	102166	4,4	372,93
7	102	7,50	999,7	102000	4,36	372,89
8	82,5	6,07	808,6	101809	4,31	372,84
9	56	4,12	548,8	101549	4,24	372,77
10	23	1,69	225,4	101225	4,15	372,68
Podciśnienie	h'	h"	p'	p=b+p'	τ	T
nr pomiaru	[mmH20]	[mmHg]	[Pa]	[Pa]	[K]	[K]
1	221	16,25	2166,0	98834	3,46	371,88
2	195,5	14,38	1916,0	99084	3,57	371,93
3	178,5	13,13	1749,4	99251	3,61	372,00
4	159,5	11,73	1563,2	99437	3,67	372,05
5	143,5	10,55	1406,4	99594	3,71	372,10
6	114	8,38	1117,3	99883	3,78	372,16
7	83	6,10	813,5	100187	3,86	372,21
8	69,5	5,11	681,1	100319	3,90	372,27
9	52,5	3,86	514,5	100485	3,94	372,31
10	25	1,84	245,0	100755	4,01	372,37

2. Obliczenie ciśnienie p [Pa] dla nadciśnienia p=b+p' i dla podciśnienia p=b-p'.

b-ciśnienie atmosferyczne=1010hPa

dla pierwszego punktu pomiarowego:p=101000+2018,9=103019Pa

3. Wykres p=f(
   )
   

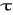
4. Odczyt z wykresu p=f(T) temperatury wrzenia wody T_b odpowiadającą ciśnieniu atmosferycznemu b.
   
   T_b=T=372,63K
   

5. Obliczenie na podstawie wykresu p=f(T) metodą graficzną współczynnika prężności pary
   .
   
   
   
   
   
   

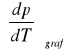
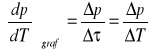
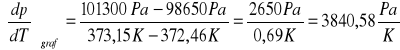
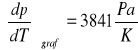
6. Współczynnik
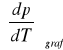
   obliczyłam metodą najmniejszych kwadratów wykorzystując funkcję REGLINP w Excelu.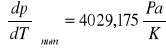
   
   
   
   
   

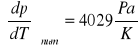
7. Wiedząc, że molowe objętości wody w stanie pary V^β i cieczy V^α wynoszą
   V^β=30,062⋅10^-3 m³mol^-1, V^α=0,019⋅10^-3 m³mol^-1 obliczam z przekształconego równania Clausiusa-Clapeyrona molową entalpię parowania ΔH_par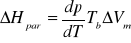
   
   
   
   
   
   
   
   
   

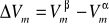
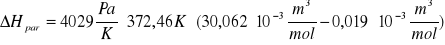
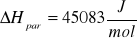
8. Obliczam molową entropię parowania wody ΔS_par w temperaturze T_b
   
   
   
   
   
   
   
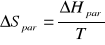
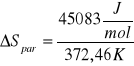
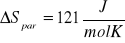
   Wartość wynikająca z równania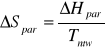
   dla wielu cieczy wynosi 88 J/molK.
   Uzyskana przeze mnie wartość molowej entalpii parowania wody jest wyższa. Wynika to z tego, że odstępstwa od tej reguły wykazują związki ulegające asocjacji. We wszystkich cieczach ( również w wodzie) wykazujących większe wartości entropii parowania, występuje asocjacja cząsteczek przez wiązanie wodorowe. W przypadku wody dla T_ntw=373K i ΔH_par=40656J/mol molowa entropia parowania wody ΔS_par wynosi 109J/mol.
   

Nadciśnienie	h'	hHg	p'	p=b+p'	τ	T
nr pomiaru	[mmH20]	[mmHg]	[Pa]	[Pa]	[K]	[K]
1	283	20,81	2773,6	101424	4,25	373,15
2	188	13,82	1842,5	100493	4,03	372,93
3	167,5	12,32	1641,6	100292	3,99	372,89
4	144	10,59	1411,3	100061	3,92	372,82
5	125	9,19	1225,1	99875	3,88	372,78
6	104	7,65	1019,3	99669	3,83	372,73
7	85	6,25	833,1	99483	3,77	372,67
8	65	4,78	637,0	99287	3,73	372,63
9	43	3,16	421,4	99071	3,68	372,58
10	24	1,76	235,2	98885	3,62	372,52

Nadciśnienie	h'	hHg	p'	p=b+p'	τ	T
nr pomiaru	[mmH20]	[mmHg]	[Pa]	[Pa]	[K]	[K]
1	210	15,44	2058,1	96592	2,98	371,88
2	188,5	13,86	1847,4	96803	3,03	371,93
3	168	12,35	1646,5	97003	3,10	372,00
4	148	10,88	1450,5	97199	3,15	372,05
5	128	9,41	1254,5	97396	3,20	372,10
6	106,5	7,83	1043,8	97606	3,26	372,16
7	88	6,47	862,5	97788	3,31	372,21
8	64	4,71	627,2	98023	3,37	372,27
9	48,5	3,57	475,3	98175	3,41	372,31
10	26	1,91	254,8	98395	3,47	372,37

Celem ćwiczenia było wyznaczenie molowej entalpii i entropii parowania wody na podstawie pomiaru temperaturowego współczynnika prężności pary. Współczynnik prężności pary wyznaczony metodą graficzną wynosi 3841 Pa/K, a metodą numeryczną 4029 Pa/K. Różnica pomiędzy tymi dwiema wartościami wynika ze zbyt małej precyzji wykreślania wykresu i późniejszego odczytu wartości. Dlatego też dalsze obliczenia opierają się na wartości temperaturowego współczynnika prężności pary obliczonej metodą numeryczną. Wyliczona wartość molowej entalpii parowania ΔH_par wynosi 45083 J/mol natomiast molowa entropia parowania wody ΔS_par wynosi 121 J/mol K. Wyniki różnią się od wartości tablicowych (dla wody), gdzie ΔH_par=40,7kJ/mol (p=1atm) a ΔS_par=109 J/molK (t=25°C). Różnice te wynikają z warunków w jakich przeprowadzony został pomiar (p=986,5hPa i t=23°C) oraz z błędów popełnianych podczas odczytu wysokości słupa wody (odczytujący mógł patrzeć pod różnym kątem i z różnej wysokości).

3

---