Marta Wypych, Mateusz Jankowski 14.03.2013

WNoŻ

Towaroznawstwo

Grupa I

Zespół 6

Sprawozdanie 55

Temat: Wyznaczanie współczynnika przewodnictwa cieplnego

Cel: wyznaczenie współczynnika przewodnictwa cieplnego

• CZĘŚĆ TERORETYCZNA

Przepływ energii między ciałami może odbywać się przez

• przewodzenie

• unoszenie

• promieniowanie

jako odrębny sposób utraty energii przez ciecze wymienia się ponadto parowanie.

Warunkiem przepływu ciepła jest różnica temperatur, dla konwekcji oraz przewodzenia musi istnieć materialny ośrodek kontaktujący. Przenoszenie energii przez promieniowanie odbywa się również w próżni.

Przewodzenie energii zwanej ilością ciepła, polega na tym ze cząsteczki ciała o wysokiej temperaturze, a więc dużej średniej energii kinetycznej wprawiają za pośrednictwem sił międzymolekularnych w intensywniejsze drgania cząsteczki ciała o niższej temperaturze, czyli przekazują im część własnej energii kinetycznej. W ten sposób temperatura drugiego ciała wzrasta a pierwszego maleje. Proces ten stopniowo się rozszerza i trwa tak długo aż temperatury obu ciał się zrównają. Jeżeli chcemy aby źródło energii zachowało stałą oraz wyższą temperaturę musimy jego energię uzupełniać. W tym celu przekształcamy najczęściej energię uzupełnić. W tym celu przekształcamy najczęściej energię wiązań chemicznych lub energię elektryczną w energię ruchu drgającego. W ten sposób zapewniamy ciągły przepływ energii w kierunku ciała o niższej temperaturze.

Pod względem technicznym ciała można podzielić na przewodniki, izolatory, półprzewodniki. Kryterium takiego podziału stanowi wartość energii przenoszonej przez poszczególne ciała w jednostce czasu i w tych samych warunkach. Szczególnie dobrze energia przekazywana jest przez drgania sieci krystalicznej, zwłaszcza w metalach. Łatwość przekazywania energii przez metale jest szczególnie duża. Dużej koncentracji swobodnych elektronów metale zawdzięczają też dobre przewodnictwo elektryczne. Zachodzi przy tym również dość znaczna dyfuzja elektronów. Zachodzi przy tym również dość znaczna dyfuzja elektronów o wyższych energiach drgań w kierunku odwrotnym. Zjawisko nie jest jednak symetryczne ze względu na nieco różną energię drgań w miejscach o różnych temperaturach ciała. Udział w przenoszeniu elektronów w przenoszeniu energii jest zresztą niewielki.

Jeżeli przez dany przekrój poprzeczny ciała przepływa w jednakowych odstępach czasu jednakowa ilość energii, to przepływ nazywamy ustalonym. Ilość ciepła przeprowadzanego wzdłuż odcinka x w jednostce czasu jest wprost proporcjonalna do pola przekroju S oraz różnicy temperatur na tym odcinku, a odwrotnie proporcjonalna do długości tego odcinka ponadto zależy w dużej mierze od rodzaju materiału.

Powyższy opis jest przybliżaną treścią równania Fouriera:

Gdy
dąży do zera, wówczas stosunek
nazywamy gradientem temperatury.

W podręcznikach powyższy wzór bywa nazywany równaniem transportu energii. Występujący na ogół w tym równaniu znak minus przed współczynnikiem
nie oznacza ujemnej wartości tego współczynnika, lecz wiąże się z tym, że gradient temperatury oznacza nie spadek a wzrost temperatury. Kierunek jest zatem ten sam co kierunek ruchu energii, ale zwrot przeciwny.

Współczynnik proporcjonalności
nazywamy współczynnikiem przewodnictwa cieplnego lub przewodnictwem właściwym materiału. Wyznaczenie współczynnika
przewodności jest treścią tego ćwiczenia. Z równania wynika definicja współczynnika przewodności cieplnej.

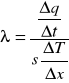
oznacza ilość energii przepływającej w jednostce czasu przez powierzchnię 1 m², prostopadłą do kierunku przepływu energii, przy spadku temperatury wynoszącym 1K na 1m.

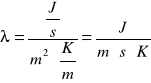
Dla cieczy wartości współczynnika
są ok.100 razy mniejsze od przeciętnej dla ciał stałych, a dla gazów - około 10 razy mniejsze niż dla cieczy. Współczynnik
wykazuje pewną zależność od temperatury. Na ogół rośnie z temperaturą, często jednak maleje, a nawet może mieć ekstrema.

Do wyznaczenia przewodnictwa cieplnego materiałów źle przewodzących energię np. materiałów sypkich lub cieczy. Badany materiał znajduje się w szczelinie pomiędzy dwoma metalowymi współosiowymi walcami. Wewnętrzny walec nagrzewany jest od grzejnika elektrycznego i przekazuje energię do walca zewnętrznego przez warstwę badanego ciała. Z równania Fouriera dochodzimy, za pomocą rachunku całkowego, do wyrażenia na

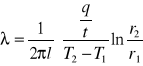
Ilość ciepła przekazywaną ciału badanemu przez grzejnik elektryczny w ciągu każdej sekundy obliczamy ze wzoru:

Gdzie:

współczynnik sprawności

U - napięcie

I - natężenie prądu

Podstawiając wyrażenie do równania otrzymujemy

Temperatury T₁ i T₂ mierzymy termometrami rtęciowymi lub wycechowanym termografem umieszczając jedno ze spojeń na miejscu termometru T₁, drugie w miejscu termometru T₂. Wskaźnikiem będzie galwanometr, którego skala może być opisana w jednostkach temperatury lub w jednostkach prądu, przy czym powinna być dołączona krzywa cechowania termoogniwa z której można odczytać różnicę temperatur. Zatrzymanie się galwanometru jest informacja że T₂ - T₁= const, czyli że przepływ energii jest już ustalony.

Wystarczy teraz odczytać wskazanie galwanometru i przerwać ćwiczenie.

Zagadnienie przewodnictwa cieplnego jest również ważne w budownictwie jak i w kuchni oraz w wielu dziedzinach przemysłowych. Ze względu na szczególne zastosowanie tego zjawiska w procesach wewnętrznej i zewnętrznej regulacji termicznej zarówno organizmu człowieka jak i zwierząt.

Wykonanie pomiaru przepisać:

Obliczenia: wzór roboczy 4.54

Wzór z zdj.

Tabela nr 1

r1	r2	l	U	I	T1	T2	T

---