Wydział WNiG	Michał Kubik Jakub Molęda Łukasz Czerwik	Rok II	Grupa 2	Zespół 2/1
	Temat: Wyznaczanie współczynnika filtracji przy przepływie przez ośrodek porowaty.			Nr ćwiczenia 4

1. Cel ćwiczenia.

Celem ćwiczenia jest zbadanie zmienności przepływu cieczy przez ośrodek porowaty przy zmianie wysokości zbiornika z wodą, oraz na pomiarze ciśnienia w 10 punktach rury z ośrodkiem porowatym.

2. Wprowadzenie.

Należy zmierzyć ciśnienie w 9 punktach rury z ośrodkiem porowatym (punkty 0 i 1 należy odrzucić) dla 6 różnych wydatków przepływu, tj. 6 różnych położeń ruchomego zbiornika przelewowego dla stałego ośrodka porowatego (rura A).

3. Podstawy teoretyczne.

Porowatość jest to właściwość substancji stałych polegająca na istnieniu w nich otwartych lub zamkniętych pustych przestrzeni, tzw. porów. Porowatość ośrodka zależy od wielkości ziaren między, którymi płynie medium. 

Zakłada się, że transport cieczy następuje w wyniku gradientów ciśnienia i sił grawitacyjnych wyrażonych przez równania przepływu cieczy Darcy'ego. Przyjmuje się przy tym, że ośrodek porowaty jest traktowany jako ciało stałe.

Tabela pomiarów:

wysokość [mm] nr rurki	h1	h2	h3	h4	h5	h6
1	504	530	562	628	691	878
2	494	518	550	610	676	857
3	401	423	450	503	558	709
4	344	362	386	432	478	600
5	288	303	322	360	400	510
6	233	246	262	292	375	414
7	168	178	190	215	238	304
8	109	115	123	140	155	202
9	49	52	54	64	70	95
Czas t [s]	29	27	25	23	21	16

4. Obliczenia.

Obliczanie wydatku i prędkości przepływu:

- wzór na wydatek, gdzie: t - czas, V - objętość

Wzór na prędkość filtracji:

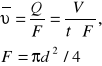
, gdzie d = 0,04 m - średnica rurki

Lp	Objętość: V [cm^3]	t [s]	Wydatek Q [m^3/s]	Prędkość υ [m/s]
1	100	29	3,45 *10^-6	2,74 *10^-3
2	100	27	3,70 *10^-6	2,95 *10^-3
3	100	25	4 *10^-6	3,18 *10^-3
4	100	23	4,3*10^-6	3,46 *10^-3
5	100	21	4,7*10^-6	3,79 *10^-3
6	100	16	6,25*10^-6	4,98 *10^-3

Z prawa Darcy'ego

J - spadek hydrauliczny

k - współczynnik filtracji

υ- prędkość filtracji

Obliczanie spadku J_i hydraulicznego ze wzoru:

Lp.	∆h [m]	L [m]	υ i [m/s]	Ji [bezw]
1.	0,056	1,12	2,47 *10^-3	0,05
2.	0,059	1,12	2,95 *10^-3	0,053
3.	0,063	1,12	3,18 *10^-3	0,056
4.	0,07	1,12	3,46 *10^-3	0,062
5.	0,077	1,12	3,79 *10^-3	0,068
6.	0,097	1,12	4,98 *10^-3	0,087

Wartość współczynnika kierunkowego „a":

Odchylenia standardowego:

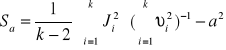
= 149,43

Z prawa Darcy'ego współczynnik filtracji k:

k = a^-1 = 0,0556 [m/s]

5. Wnioski.

Prędkość przepływu jest proporcjonalna do spadków hydraulicznych. Prędkość filtracji jest wprost proporcjonalna do wydatku i odwrotnie proporcjonalnie do powierzchni przekroju. Im wyżej znajdował się zbiornik z wodą tym wyższe były ciśnienia w poszczególnych punktach rurki i większy wydatek przepływu.

---