[26] Kąty Eulera i macierz obrotu

Euler zauważył, że dowolne położenie czworościanu w przestrzeni może być reprezentowane poprzez trzy kąty, tj. obroty czworościanu nieruchomego względem pewnych osi i przy pomocy tylko trzech kątów obrotu w pewnych płaszczyznach doprowadzą do pokrycia się ostrosłupa nieruchomego z ruchomym.

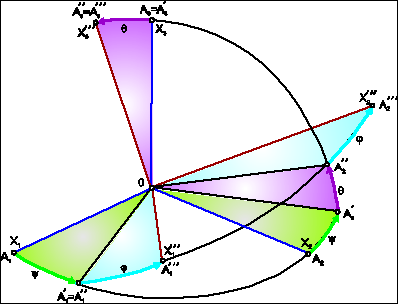
Rys. 6.5. Kąty Eulera

Kąty Eulera przedstawiono na rys. 6.5 (patrz [V. E. Zhuravlev, „Osnowy Tieoreticheskoy Mechaniki”. Fizmatlit, Moskva 2001])

Czworościan 0A₁A₂A₃ po złożeniu trzech płaskich obrotów kolejno o kąty ψ, θ i ϕ znajduje się w położeniu
. Pierwszy obrót o kąt ψ (kąt precesji) odbywa się w płaszczyźnie 0A₁A₂ wokół osi 0A₃. Drugi obrót o kąt θ (kąt nutacji) zachodzi w płaszczyźnie
wokół osi
. Na koniec dokonujemy obrotu o kąt ϕ (kąt obrotu właściwego) w płaszczyźnie
wokół osi
. Kolejność obrotów czworościanu można schematycznie przedstawić w następujący sposób:

(6.49)

Po zrzutowaniu wersorów kolejnych układów współrzędnych na osie układów przed kolejnym obrotem otrzymujemy:

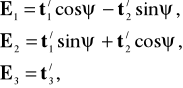
(6.50)

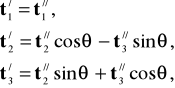
(6.51)

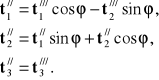
(6.52)

Działania opisane wzorami (6.50) - (6.52) można przedstawić w postaci:

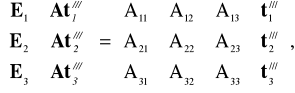
(6.59)

gdzie:

(6.60)

jest tensorem obrotu będącym wynikiem działania trzech tensorów obrotu Ψ, Θ, φ.

---