POLITECHNIKA CZĘSTOCHOWSKA

LABORATORIUM FIZYKI WSPÓŁCZESNEJ

TEMAT: Wyznaczanie grubości cienkiej folii aluminiowej metodą pochłaniania promieni β.

Ćw.wykonali:

Dariusz Frydrych

Paweł Łakomy

Wydz. Elektryczny

grupa II.

I.Wstęp teoretyczny.

Rozpad β. Przechodzenie promieniowania β przez materię.

Pojęcie rozpadu β odnosi się do trzech procesów jądrowych, a mianowicie do rozpadu β^- związanego z emisją elektronu rozpadu β⁺ pozytonu , i tzw. wychwytu elektronu , polegającego na wychwycie przez jądro jednego z elwktronów powłoki atomu . Najczęściej zachodzi tzw. wychwyt K, to znaczy przejście elektronu z najbliższej jądru powłoki K.

W procesie rozpadu β jądro wyjściowe traci określoną ilość energii , która powinna być jak się wydaje , uniesiona tylko przez cząstkę β . W związku z tym cząsti β powinny posiadać określoną jerdną lub kilka wartości energii. Mówiąc inaczej widmo promieniowania β powinno mieć charakter liniowy . Jednakże z doświadczenia wynika , widmo jest ciągłe , tzn. energia emitowanych cząstek przyjmuje wszystkie wartości od zera aż do do pewnej wartości maksymalnej E_max chociaż jądro traci w każdym akcie rozpadu β dokładnie określona energię równą właśnie E_max.

Ten paradoksalny fakt wyjaśniono , zakładając, że w procesie rozpadu β oprócz elektronu wylatuje jeszcze jedna cząstka (nazwana neutrinem) unosząca energię E_ν taką , że w każdym elementarnym akcie emisii elektronu spełniona jest zasada zachowania energii:

E_max=E_β+E_ν

gdze: E_β - energia emitowanego elektronu.

Rozpad β jest związany z przejściem jednego z neutronów jądra w proton z jednoczesną emisja elektronu i antyneutrina lub przejściem protonu w neutron z jednoczesną emisja pozytonu i neutrina.

Odpowiednie reakcje można zapisać w postaci:

n¹₀- n¹₀--p¹₁+e⁰_-1+ν⁰₀ - rozpad β^-

p¹₁--n¹₀+ e⁰₊₁ + ν⁰₀ - rozpad β⁺.

Trzeci rozpad β, a mianowicie wychwyt elektronu, zwiazany jest z rozdziałem energii między

jądro pochodne a neutrino .

Schemat tego procesu ma postać :

p¹₁ + e⁰_-1 -- n¹₀ + ν⁰₀ .

Przemianie protonu w jądrze towarzyszy zamkniecie elektronu z powłoki K . Z doświadczewnia wynika , że wychwytowei energii towarzyszy charakterystyczne promieniowanie rendgenowskie

odpowiadające linii K widma danego piewiastka.

W widmie β oprócz części ciagłej obserwuje się również monoenergetyczne piki. Obecność ich zwiazona jest z tzw. konwersją wewnętrzną , przy której wzbudzone jądro atomowe przechodzi do stanu podstawowego o niższej energii , przekazując bezpośrednio energię wzbudzenia elektronowi orbitalnemu (nazywa się elektronami konwersii).

Energia takiego elektronu jest mniejsza od energii kwantu γ emitowanego z jądra o wartoscxi energii wiązania elektronu na orbicie , z której został wyrzucony.

Licznik Geigera Mullera.

L

W

W stanie normalnym gaz wypełniający licznik nie przewodzi prądu elektrycznego.

Jeżeli jednak do wnętrz licznika dostanie siecząstka nałdowana , jonizująca gaz ewówczas oderwanie od atomów gazu elektrony przyciągane przez dodatnio naelektryzowanu drut uzyskuje w silnym polu elektrostatycznym panującym wokół anody tak dóże prędkosci , że przy zdeżeniach z obojętnymi atomami gazu jonizują je.

Powstałe elektrony z kolei rozpędzają się i wywołują dalsza jonizację. W bardzo krótkim czasie powstaje lawina elektronów , która przenosi stosunkowo duży ładunek.

Przez licznik , a więc w całym obwodzie przepływa prąd elektryczny wywołujący krótkotrwały impuls .

Wywołanie lawinowe daje zwiększenie liczby elekltronów zbieranych przez anodę wywołując impuls w liczniku.

Za pomocą licznika można również rejeatrować fotony , które wybijają ze ścianek licznika lub z atomów gazu wypełniającego licznik.

II. Schemat blokowy aparatury pomiarowej.

II

III I

gdzie: I - licznik Geigera Mullera

II - zasilacz wysokiego napięcia ZWN - 42

III - przelicznik PT - 72

III.Tabele pomiarowe.

Folia nr.	Ilość impulsów m [imp]	Ilość impilsów/s z=m/t [imp/s]
bez floi	6913	34.56
1	6868	34.34
2	6566	32.83
3	6446	32.23
4	6251	31.25
5	5964	29.82
6	5717	28.58
7	5375	26.87
8	5346	26.73
9	5398	26.99
10	5052	25.10
X	5529	27.64

Wyznaczanie gęstości powierzchniowehj folii d₀ .

n	G [mG]	m [g]	S [cm^2]	d^0=m/S [g/cm^2]
1	12.2	0.0122	4	0.00395
2	11.8	0.0118	4	0.00295
3	11.8	0.0118	4	0.00295
4	12.6	0.1260	4	0.00320
5	12.2	0.0122	4	0.00310
6	11.8	0.1228	4	0.00295
7	12	0.0120	4	0.0030
8	12.8	0.0128	4	0.0032
9	12	0.0120	4	0.0030
10	12.2	0.0122	4	0.00305

IV. Opracowanie wyników.

n	k	z	ln(z)	k^2	k ln(z)
1	0	34.52	3.52	0	0
2	1	32.83	3.49	1	3.49
3	2	32.23	3.47	4	6.94
4	3	31.25	3.44	9	10.32
5	4	29.82	3.39	16	13.56
6	5	28.58	3.35	25	16.75
7	6	26.87	3.29	36	19.74
8	7	26.73	3.28	49	22.96
9	8	26.99	3.29	64	26.32
10	9	25.10	3.22	82	28.98
	∑ki=45		∑ln(zi)= 33.74	∑ki^2=285	∑kilnzi= 149.06

Obliczenia.

10A-45B=33.74

A-45-285B=149.06

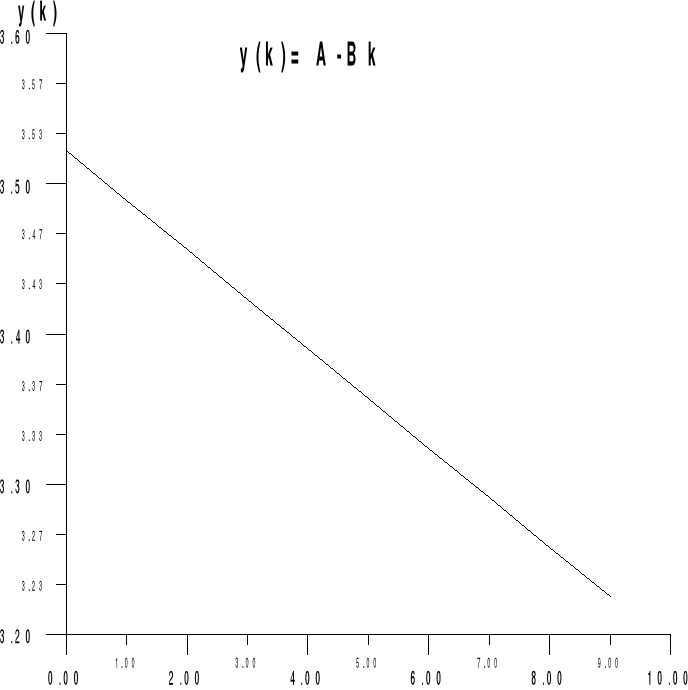
Wyznaczenie funkcji y(k)=A-B y(0) =

V. Masowy współczynnik pochłaniania.

VI.Wyznaczenie grubości folii.

VI. Wnioski.

Przeprowadzone pomiary pozwoliły nam na wyznaczenie z dość dużą dokładnością grubości folii aluminiowej .

Cała istota ćwiczenia opierała się na wykożystaniu promieni β przechodzących przez kolejne próbki folii.

Mósimy zatem zwrócić uwagę na to, że że natężenie promieni β przechodzących przez warstwy folii ulega osłabieniu na skutek pochłaniania i rozpraszania promieniowania.

Zmniejszwnie natężenia promieniowania jest proporcionalne do grubości folii.

Z otrzymanych wyników możemy wywnioskować ,że do trzeciego miejsca po przecinku dla wszystkich dadanych próbek otrzymalismy takie same wyniki , dalej pojawiają się już niewielkie róznice.

Głównym procesem odpowiedzialnym za straty energii czząstek β w osrodku jest tzw. promieniowanie hamowania.

Ze względu na małą masę elektrony doznają solnego hamowania. W procesie tym prędkości ich maleją.

---