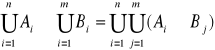[DM 10]
[1/10] Niech A = {1, 2, 3, 4}, B = 2, C = ∅, D = {1, 4, 5}, E = {3, ∅}, F = {{1}, 2, {3}, 4}. Dla każdej pary X, Y ∈ {A, B, C, D, E, F} odpowiedz na pytanie czy:
(a) X ⊆ Y
(b) X ∈ Y
[2/10] Czy istnieje zbiór, który nie posiada podzbioru właściwego?
[3/10] Czy to prawda, że jeśli A ⊆ B ∪ C to A ⊆ B lub A ⊆ C. ?
[4/10] Wyznacz zbiór ![]()
, gdzie P(n) jest spełnione gdy n jest liczbą pierwszą, a Ai = {i, i + 1, 2i}. (Nie mylić z {i, i + 1,..., 2i}).
[5/10] Ile elementów ma zbiór:
(a) {0, 1}3 ∪ {0, 1, 2}2
(b) {{0,1}}3
(c) {∅, {∅}} × ∅
(d) {0, {0, {0, {0}}}} × {1, {9, {9, {7}}}}
[6/10] Na cztery różne, przedstawione na wykładzie sposoby (bezp. z def., metodą 0-1, za pomocą diagramów Venna, w oparciu o prawa algebry zbiorów) udowodnij, że:
(a) A ∩ B ⊆ A ∪ B
(b) A \ (A \ B) = A ∩ B
(c) A \ (B ∩ C) = (A \ B) ∪ (A \ C)
(d) A \ (B \ (C \ D)) = (A \ B) ∪ ((A ∩ C) \ D)
[7/10] Czy dla dowolnej skończonej liczby zbiorów A1, A2,..., An można narysować poprawny diagram Venna?
[8/10] Sprawdź, czy dla dowolnych zbiorów A, B, C zachodzi:
A × (B ∪ C) = (A × B) ∪ (A × C)
A ∩ (B × C) = (A ∩ B) × (A ∩ C)
A × (B \ C) = (A × B) \ (A × C)
A \ (B × C) = (A \ B) × (A \ C)
(A × B) ∩ (B × A) = (A ∩ B) × (B ∩ A)
[9/10] Wyznacz ![]()
oraz ![]()
dla rodzin zbiorów (zakładamy, że 0 ∈ R+):
At = {x : 0 < x ≤
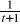
}At = {x :
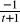
< x <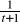
}At = {(x, y) : x2 + y2 ≤ t2}
At = {(x, y) : x2 ≤ t2y2
[10/10] Które z poniższych implikacji są prawdziwe? Co można powiedzieć o implikacjach odwrotnych?
A = B ⇒ A ∩ C = B ∩ C
A = B ⇒ A ∪ C = B ∪ C
A = B ⇒ A \ C = B \ C
A = B ⇒ Ac = Bc
A ⊆ B ⇒ A ∩ C ⊆ B ∩ C
A ⊆ B ⇒ A ∪ C ⊆ B ∪ C
A ⊆ B ⇒ A \ C ⊆ B \ C
A ⊆ B ⇒ Ac ⊆ Bc
[11/10] Korzystając z praw algebry zbiorów oraz z wyników poprzedniego zadania wykaż, że:
A ∩ B = A ⇔ A ∪ B = B ⇔ A \ B = ∅ ⇔ Ac ∪ B = X
((A ⊆ B) ∧ (C ⊆ D)) ⇒ A \ D ⊆ B \ C
[12/10] Wykaż, że
[13/10] Które z poniższych implikacji lub równoważności są prawdziwe? Co można powiedzieć o implikacjach odwrotnych?
[(A ∩ B) \ C = ∅] ⇒ [(A ∪ B) \ (A ∪ C) = B \ C]
[A \ (A \ B) = B] ⇒ [C ⊆ B → C ⊆ A]
[AC ∩ BC = A ∩ B] ⇔ [AC = B]
Wyszukiwarka
Podobne podstrony:
DEgz2-2007-rozw, AA informatyka - studia, cwiczenia i egzaminy
DEgz1-2006, AA informatyka - studia, cwiczenia i egzaminy
DEgz1-2007, AA informatyka - studia, cwiczenia i egzaminy
DEgz2-2010 rozw, AA informatyka - studia, cwiczenia i egzaminy
Zad02 relacje binarne, AA informatyka - studia, cwiczenia i egzaminy
DEgz2-2009 rozw, AA informatyka - studia, cwiczenia i egzaminy
Zad03 relacje binarne-domkniecia, AA informatyka - studia, cwiczenia i egzaminy
Zad04 zliczanie, AA informatyka - studia, cwiczenia i egzaminy
DEgz2-2005, AA informatyka - studia, cwiczenia i egzaminy
DEgz1-2008 zakres 2007-2008, AA informatyka - studia, cwiczenia i egzaminy
DEgz2-2010, AA informatyka - studia, cwiczenia i egzaminy
Karta Inform MatElem, AA informatyka - studia, cwiczenia i egzaminy
DEgz1-2009, AA informatyka - studia, cwiczenia i egzaminy
DEgz1-2005, AA informatyka - studia, cwiczenia i egzaminy
DEgz2-2008, AA informatyka - studia, cwiczenia i egzaminy
więcej podobnych podstron