I OPRACOWANIE MATERIAŁU STATYSTYCZNEGO

Materiał statystyczny otrzymujemy w wyniku obserwacji statystycznej ma postać nieuporządkowanego zbioru danych o poszczególnych jednostkach statystycznych i jest on określany jako surowy (indywidualny) materiał statystyczny. Materiał ten nie może być przedmiotem analizy, porównań i wyciągania wniosków, gdyż zawiera informacje o poszczególnych jednostkach, a nie o całej zbiorowości statystycznej. Dlatego materiał ten w kolejnym etapie badania statystycznego podlega opracowaniu (uporządkowaniu).

Opracowanie materiału obejmuje: grupowanie statystyczne i zliczanie materiału statystycznego. W zależności od możliwości instytucji prowadzącej badanie statystyczne opracowanie materiału statystycznego może być prowadzone przy wykorzystaniu różnych metod organizacyjno - technicznych. Jeżeli badanie statystyczne jest prowadzone przez małe przedsiębiorstwo, wówczas większość czynności związanych z opracowaniem materiału statystycznego jest prowadzona ręcznie, bądź z wykorzystaniem komputera osobistego. Jeżeli natomiast badanie jest prowadzone przez wyspecjalizowaną instytucję, wówczas do opracowywania materiału statystycznego wykorzystuje się specjalistyczne urządzenia.

W wyniku opracowania surowego materiału statystycznego zostaje on przekształcony w materiał zbiorczy, charakteryzujący całą badaną zbiorowość bądź próbę.

Grupowanie materiału statystycznego

Grupowanie statystyczne - polega na podziale całej zbiorowości statystycznej na mniejsze jej części, czyli jednolite grupy jednostek. Wyodrębnienie tych grup dokonywane jest na podstawie jednoznacznych kryteriów. Tymi kryteriami są warianty cechy statystycznej. Jeżeli cecha statystyczna ma charakter naturalny (np. płeć), wówczas grupowanie statystyczne ma również naturalny charakter (np. podział mieszkańców Warszawy na mężczyzn i kobiety). Niekiedy jednak kryteria podziału zbiorowości grup nie mają charakteru naturalnego, wtedy podmiot prowadzący badanie musi zdecydować jakie mniejsze zostaną wyodrębnione w ramach badanej zbiorowości. Grupowanie statystyczne pozwala na uporządkowanie materiału statystycznego i zapewnia jego porównywalność. Celem grupowania statystycznego jest wskazanie podobieństwa i różnic występujących w badanej zbiorowości statystycznej oraz sformułowanie obiektywnych wniosków ogólnych. Decydujące znaczenie, przy dokonywaniu grupowania statystycznego, ma cel badania statystycznego.

Dokonanie prawidłowego grupowania statystycznego wymaga przestrzegania niżej wymienionych zasad:

• Wykaz klasyfikacyjny (wykaz wariantów cech) musi być skonstruowany w taki sposób, aby żadna jednostka statystyczna poddana badaniu nie znalazła się poza wykazem - jest to zasada grupowania wyczerpującego;

• Wykaz musi być skonstruowany w taki sposób, aby żadna jednostka statystyczna poddana badaniu nie była zaliczona jednocześnie do dwóch grup (wariantów) - jest to zasada grupowania rozłącznego;

• Jeżeli jednostki statystyczne są bardzo zróżnicowane pod względem wartości cechy, należy tworzyć więcej przedziałów klasowych, tak aby każdy z nich zawierał jednostki o małym zróżnicowaniu wartości cechy;

• Grup nie powinno być zbyt dużo, dlatego jeżeli niektóre warianty cechy występują u niewielkiej liczby jednostek, możliwe jest stworzenie grup zbiorczych, które określa się jako pozostałe;

• Przy badaniach powtarzalnych nie powinno się zmieniać wykazu klasyfikacyjnego, dzięki czemu możliwie będzie porównywanie wyników tych badań.

Zliczanie materiału statystycznego - czyli metody techniczno - organizacyjne opracowania materiału statystycznego

Po dokonaniu grupowania statystycznego następuje zliczanie materiału, czyli ustalenie liczebności poszczególnych grup. Efektem zliczania materiału statystycznego jest stwierdzenie, ile jednostek statystycznych przypada na poszczególne warianty cechy przyjęte w wykazie klasyfikacyjnym.

Zliczanie bezpośrednie (ręczne) jest stosowane wówczas, gdy badane zbiorowości mają małą liczebność i gdy podział jednostek na grupy jest prosty. Zliczanie bezpośrednie polega na zliczeniu i zanotowaniu liczby jednostek statystycznych posiadających określony wariant i cechy.

Zliczanie sposobem kreskowym wymaga skonstruowania tablicy roboczej, w której pionowymi kreskami zaznacza się wystąpienie określonego wariantu cechy. Ułatwieniem jest zastosowanie jako piątej - kreski poziomej, która przecina cztery kreski pionowe. W taki sposób każda wiązka oznacza pięć jednostek obserwacji. W celu sprawdzenia prawidłowości zliczania materiału statystycznego sposobem kreskowym porównuje się liczbę kresek z liczebnością badanej zbiorowości. Jednak nawet w sytuacji, gdy liczba kresek jest równa liczebności zbiorowości, mógł zostać popełniony błąd, że kreska została postawiona przy niewłaściwym wariancie cechy.

Zliczanie sposobem kartkowym (uwzględnianie tylko w niektórych pozycjach literatury) polega na posegregowaniu indywidualnego materiału statystycznego w postaci wypełnionych formularzy statystycznych na stosy o jednakowych wariantach cechy. Po zliczeniu formularzy znajdujących się w każdym stosie zapisuje się ich liczbę. Zliczanie sposobem kartkowym może być stosowane jedynie wówczas, gdy informacje o poszczególnych jednostkach podlegających badaniu zostały zebrane na indywidualnych formularzach.

Zliczanie sposobem maszynowym jest stosowane, gdy liczebność badanej zbiorowości jest duża. Jest rzadko stosowana ze względów finansowych, wysoki koszt maszyn. Ten sposób zliczania materiału statystycznego jest stosowany przez instytucje, które prowadzą wiele różnych badań statystycznych, w których można wykorzystać zakupione maszyny. Dokonując zliczenia sposobem maszynowym należy wykonać symbolizację materiału statystycznego.

II METODY PREZENTACJI DANYCH STATYSTYCZNYCH

Przedział to zbiór elementów danego zbioru częściowo uporządkowanego, zawartych między dwoma ustalonymi elementami tego zbioru, nazywanymi początkiem i końcem przedziału.

Przedział nazywa się domkniętym, gdy oba jego końce doń należą, zaś otwartym gdy żaden nie należy. Jeśli do przedziału należy tylko początek albo tylko koniec, przedział taki nazywa się, odpowiednio, lewostronnie albo prawostronnie domkniętym.

A. Tabelaryczna prezentacja danych statystycznych - szeregi i tablice

Szereg statystyczny - ciąg wielkości statystycznych, uporządkowanych wg określonego kryterium

Wśród szeregów statystycznych wyróżnia się szeregi:

• jednocechowe (jednowymiarowe) - obejmują wartości liczbowe jednej cechy, czyli próby jednowymiarowe (np. cecha - przychody z podatków z nieruchomości; jednostki - przedsiębiorstwa),

• wielocechowe (wielowymiarowe) - uwzględniają wartości liczbowe dwu lub więcej cech, czyli próby wielowymiarowe (np. cechy - liczba złożonych zeznań podatkowych, liczba prywatnych działalności gospodarczej, opłaty z działalności gospodarczej; jednostki - osoby fizyczne prowadzące działalność gospodarczą).

Wśród jednych i drugich wyodrębnia się szeregi szczegółowe i strukturalne. W szeregach pierwszego rodzaju podawane są szczegółowe wartości liczbowe cech jednostek wchodzących w skład próby jedno lub wielowymiarowej. W przypadku drugim zadawane są pewne przedziały liczbowe oraz liczby jednostek do nich zaliczanych.
Szeregi szczegółowe najczęściej mają postać szeregu surowego i wtedy jest określany jako szereg nieuporządkowany. Gdy ma on postać odpowiednio uporządkowaną dla jednej z wybranych cech według wartości rosnących (niemalejących) lub malejących (nierosnących), to wówczas otrzymuje się szereg uporządkowany.

Sposób grupowania cech zależy od: rodzaju badania (przekrojowe, czasowe), rodzaju cechy statystycznej, sposobu pomiaru oraz liczby obserwacji (szczegółowe, rozdzielcze).

Szeregiem szczegółowym nazywamy uporządkowany, wyłącznie według wartości badanej cechy, zbiór danych. Porządkowanie polega na ustawieniu wartości określonej cechy danej zbiorowości lub próby według kolejności rosnącej lub malejącej.

• Szereg szczegółowy obejmuje wartości zmiennych występujących u wszystkich jednostek badanej zbiorowości.

• Szeregiem rozdzielczym nazywamy uporządkowany i pogrupowany (według przyjętych kryteriów) zbiór informacji dotyczących badanej cechy występującej w określonej zbiorowości lub próbie. Otrzymuje się go dzieląc zbiorowość statystyczną na klasy zbiorcze według pewnej cechy i podając liczebności każdej z tych klas, zwane liczebnościami klasowymi ni, i=1,2,...,k.

Szeregi rozdzielcze mogą dotyczyć zarówno cechy jakościowej, jak i ilościowej. Charakteryzują one strukturę danej zbiorowości stąd nazywane są czasem szeregami strukturalnymi.

Kolejne kroki podczas wykonywania szeregu rozdzielczego:

• porządkujemy (jeśli to możliwe rosnąco) wartości cechy

• zliczamy ilość wystąpień danej cechy w próbie

• obliczamy częstości występowania dla każdej wartości cechy

• prezentujemy wynik w formie tabeli

Jeśli cecha ma charakter ciągły, wtedy dzielimy przedział wartości cechy na przedziały klasowe. Liczba i rozpiętości przedziałów powinny być tak dobrane, aby dawały przejrzysty obraz rozkładu. Na ogół przyjmuje się, że liczba przedziałów powinna być większa od 5 i mniejsza od 20.

Jeśli cecha ma charakter skokowy, ale liczba możliwych wartości jest bardzo duża, wtedy możemy postąpić podobnie jak w przypadku cechy o charakterze ciągłym.

• Szereg geograficzny - przedstawiają rozmieszczenie wielkości statystycznych według jednostek administracyjnych (gmin, województw w układzie terytorialnym) a także w układzie krajów i części świata.

Zbudowane z dwóch kolumn, w pierwszej z tych kolumn wymieniamy jednostki podziału zbiorowości statystycznej na mniejsze grupy. Jednostkami przedziału szeregów terytorialnych są jednostki geograficzne (terytorialne, przestrzenne), np. gmina, województwo, państwo, regiony gospodarcze, kontynenty.

W drugiej kolumnie szeregu terytorialnego informuje się o wielkości badanego zjawiska w jednostce wymienionych w pierwszej kolumnie. Szereg geograficzny pozwala na przedstawienie przestrzennego rozmieszczenia badanego zjawiska w określonym czasie.

• Szereg czasowy - (dynamiczny chronologiczny) powstaje w wyniku grupowania typologicznego i wariacyjnego, gdy podstawą grupowania jest zmiana badanego zjawiska w czasie:

- Szereg czasowy okresów - zawiera informację o rozmiarach zjawiska w krótszych lub dłuższych okresach.

- Szereg czasowy momentów - ujmuje wielkość zjawiska w danym momencie, najczęściej na początku lub końcu np. miesiąca.

Tablica statystyczna jest formą uporządkowania danych liczbowych dotyczących jednej lub więcej zbiorowości według przyjętych kryteriów.

Elementy składowe tablicy statystycznej są:

• numer

• tytuł

• właściwa treść tablicy

• objaśnienia

• źródło

 

Tytuł - określa jaka zbiorowość statystyczna jest ujęta w tablicy. Powinien być on sformułowany jasno, dokładnie i zwięźle a przy tym należycie informować o zawartej w niej treści.

Właściwa treść tablicy - zawarte są w rubrykach (kolumnach) i wierszach których sens określają główka i boczek

Główka - górna część tablicy określająca poszczególne kategorie podziału zbiorowości

Boczek - obejmuje poszczególne zbiorowości podzielone liczbowo na na kategorie wykazane w główce.

Objaśnienia - zawierają dodatkowe wyjaśnienia poszczególnych wierszy i kolumn lun całej tablicy

Źródło - mówią skąd pochodzą liczby zamieszczone w tabeli - szczególnie ważne przy wykorzystaniu wtórnego materiału statystycznego.

Kontrola materiału statystycznego. Rozróżniamy 2 rodzaje kontroli:

• kontrolę formalną materiału statystycznego obejmującą kontrolę kompletności materiału statystycznego, kontrolę zupełności zapisów oraz kontrolę zgodności rachunkowej

• kontrolę merytoryczną materiału statystycznego sprowadzającą się do kontroli logicznej poprawności zapisu

Kontrola kompletności materiału statystycznego polega na sprawdzeniu czy otrzymano materiał od wszystkich jednostek sprawozdawczych zobowiązanych do jego przesłania. Kontrola zupełności zapisu polega na sprawdzeniu czy odpowiedziano na wszystkie pytania zawarte w formularzu ankiecie lub innych materiałach statystycznych.

B Graficzna prezentacja danych statystycznych

Graficzna prezentacja danych statystycznych oznacza obrazowanie ich za pomocą różnych metod, które ogólnie można nazwać wykresami.

Wykres - szeroko stosowany środek w popularyzacji danych statystycznych. W różnej formie sporządzony wykres znacznie skuteczniej przyciąga uwagę na wystawie, w czasopiśmie czy książce, aniżeli zbiór danych zawarty w tablicy czy nawet pojedynczym szeregu statystycznym. Jest również czynnikiem ułatwiającym analizę.

Jednym z ważnych warunków skutecznego spełnienia celów stawianych wy-kresom jest ich staranne wykonanie. Duże znaczenie ma umiejętne dobranie formy wykresu do prezentowanej zbiorowości oraz kolorystyka.

Podobnie jak tablica statystyczna, każdy wykres musi mieć tytuł informujący, co przedstawia, a nadto być zaopatrzony w legendę (objaśnienia wyjaśniające znaczenie zastosowanych w nim barw, znaków, symbol; oraz przyjęta podziałkę.

Wyróżniamy następujące metody graficznej prezentacji danych statystycznych:

• Metoda liniowa - najprostsza i najłatwiejsza do sporządzenia graficzną formą prezentacji danych liczbowych. Podstawą do sporządzenia wykresu mogą być tablice lub pojedyncze szeregi statystyczne. Mogą nią być również pojedyncze wielkości nie ujęte w szeregu statystycznym, np. długość rzek w Polsce. Wielkość prezentowanego zjawiska określa właściwa dla niej, w przyjętej skali, długość linii. Wykres może być sporządzony w postaci poziomej lub pionowej.

• Metoda powierzchniowa - to graficzna forma przedstawiania danych liczbowych za pomocą figur geometrycznych lub obrazków (symboli) dostosowanych rozmiarami swojej powierzchni do wielkości zjawiska, które ilustrują. Można zastosować prezentacje pionową, jak i poziomą, dlatego, że obie będą w dobry sposób obrazować to zjawisko.

• Metoda obrazkowa - prezentowane dane liczbowe dotyczące badanej zbiorowości są, przedstawione za pomocą znaków lub obrazków (symboli) odpowiadających swoim wyglądem rodzajowi zbiorowości, która reprezentują. I tak symbolem oznaczającym samochody jest obrazek samochodu, ludność - sylwetka człowieka, lasy - obrazek drzewa itp.

Rysowanie symboli większych rozmiarów dla grup o większych liczebnościach nie wchodzi praktycznie w rachubę ze względu na trudność obliczania powierzchni figur o nieregularnych kształtach. Z tego względu za słuszną należy uznać zasadę prezentowania zróżnicowania liczebności poszczególnych grup szeregu statystycznego przez odpowiednia liczbę znaków - symboli identycznego rozmiaru. Jeżeli, dla przykładu, sylwetka jednego ucznia ma reprezentować dziesięciu uczniów objętych badaniem i ujętych w szeregu strukturalnym lub dynamicznym, to dla grupy liczącej trzydziestu uczniów trzeba wymalować trzy sylwetki.

Wykresy obrazkowe nie odznaczają się rachunkowa dokładnością. Nie to jest jednak dla nich najważniejsze. Ich celem nadrzędnym jest przyciągnięcie uwagi i skierowanie jej na prezentowane na wykresie zjawisko, co pośrednio przybliża do statystyki i jest czynnikiem jej popularyzacji. Wiele tego rodzaju wykresów spotyka się na rożnych wystawach.

• Metoda ilościowa - wielkość zjawiska zostaje zaprezentowana wielokrotnością dowolnego, łatwego do narysowania i podzielenia znaku graficznego, np.: trójkąta, koła, prostokąta.

• Metoda ilościowo - symbolowa - znana także jako metoda wiedeńska - połączenie metody obrazkowej i ilościowej. Polega na tym, ze w metodzie ilościowej zamiast znaków stosuje się małe rysunki-symbole, które przedstawiają prezentowane zjawisko. Rysunki-symbole muszą być proste, czytelne, starannie wykonane graficznie i tak dobrane, aby wyraźnie sugerowały, o jakie zjawisko chodzi.

• Podobnie jak metoda ilościowa nie jest metoda całkowicie dokładna.

• Kartogram - jest wykresem sporządzony na mapie konturowej. Kartogramy są szczegó1ną  postacią wykresów stosowana  w prezentacji szeregów terytorialnych.

Różne są środki, którymi posługujemy się w technice sporządzania kartogramów. Mogą nimi być: punkty, figury geometryczne, zakreskowane powierzchnie, symbole. Wielkość obrazowanego zjawiska na danym terenie (województwo, gmina) może tez określać kolor przypisany zjawisku o danym natężeniu.

Posługując się prostokątami lub kołami możemy jednocześnie z przedstawianiem wielkości danego zjawiska właściwego dla określonego terenu ujmować wewnętrzną jego strukturę dzieląc prostokąty lub koła na elementy składowe i odpowiednio je graficznie różnicując. Np. słupki lub koła umieszczone w poszczególnych województwach obrazujące ogólną, liczbę ludności mogą, być podzielone na części wyodrębniające płeć męską i żeńską.

Kartogramy są, częstą formą graficzną prezentacji danych statystycznych w różnych publikacjach statystycznych, niekiedy w czasopismach oraz na różnych wystawach.

• Wykresy w układzie współrzędnych

Stosowany w statystyce do graficznego przedstawiania liczbowych danych układ współrzędnych stanowi zwykle ćwiartkę. Wynika to z tego, ze w wykresach statystycznych mamy do czynienia z reguły z wielkościami dodatnimi.

Właściwymi wykresami sporządzanymi w układzie współrzędnych są. histogramy i diagramy.

Histogram jest wykresem składającym się ze słupków bezpośrednio przylegających do siebie, ustawionych na osi odciętych (x).

Na każdym histogramie może być opisany diagram. Możemy go skonstruować za pomocą linii ciągłej łącząc środki górnych boków prostokątów w histogramach.

III. ANALIZA STATYSTYCZNA

Analiza statystyczna to badanie i interpretacja zebranego materiału statystycznego w celu ujawnienia w nim określonych prawidłowości i związków oraz formułowanie na ich podstawie wniosków; obejmuje analizę struktury, dynamiki, natężenia i współzależności.

Struktura zbiorowości określona jest przez podział badanej zbiorowości statystycznej na grupy jednostek różniących się od siebie wartościami poszczególnych cech. Liczbową formą opisu struktury są liczby względne powszechnie stosowane jako wskaźnik struktury.

Miary przeciętne charakteryzują średni lub typowy poziom wartości cechy. Są to więc takie miary, wokół których skupiają się wszystkie pozostałe wartości analizowanej cechy.

Miary średnie dzielą się na dwie grupy: średnie klasyczne i pozycyjne.

Średnie klasyczne otrzymywane są droga rachunkową z uwzględnieniem wszystkich wartości szeregu statystycznego. Należy do nich głównie średnia arytmetyczna(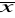
) - najczęściej stosowana w analizach statystycznych. Otrzymujemy ja w wyniku podzielenia sumy wartości cechy wszystkich jednostek zbiorowości przez liczebność zbiorowości.

Średnie pozycyjne są wartościami konkretnych wyrazów szeregu statystycznego, wyrazów wyróżniających się pod jakimś względem, tzn. zajmujących w szeregu wyraźnie określona pozycję

Najczęściej wykorzystywanymi średnimi pozycyjnymi są:

• dominanta - zwana jest również modą, wartością typową, wartością modalną lub wartością najczęstszą. Jest ona wartością cechy, która najczęściej występuje w zbiorowości badanej. Dominantę wykorzystuje się w przypadku cech niemierzalnych, jest ona jedyną miarą, która do tego służy.

• mediana - nazywana jest również wartością środkową lub też środkiem obszaru zmienności rozpatrywanej zmiennej. Jest to wartość zmiennej, która rozdziela całą populację na takie dwie równe części. W pierwszej częścią są jednostki o wartościach niższych od mediany, a w drugiej są jednostki o wartościach wyższych. Medianę obliczamy w zależności od tego, z jakiego rodzaju szeregiem statystycznym przedstawiającym informacje o wartości cechy statystycznej, mamy do czynienia oraz czy liczba jednostek statystycznych (liczebność zbiorowości) jest parzysta, czy nieparzysta.
  

Analiza dynamiki polega przede wszystkim na określeniu rozmiarów i kierunków rozwoju (zmian w czasie) badanych zjawisk, tzn. ustaleniu stopnia poziomu wzrostu lub spadku badanego zjawiska. Wstępne informacje dotyczące tendencji rozwojowych (wzrost, spadek, utrzymanie się na niezmienionym poziomie w poszczególnych okresach) uzyskujemy w wyniku przeglądu szeregów dynamicznych obrazujących zmiany badanych zjawisk w czasie.

W badaniach statystycznych jedną z najczęściej stosowanych miar dynamiki są indeksy, zwane również wskaźnikami dynamiki.

Indeks jest to wielkość stosunkowa powstała w wyniku podzielenia wielkości danego zjawiska w okresie badanym przez wielkość tego zjawiska w okresie podstawowym. Wyróżniamy indeksy:

• indywidualne (proste) - są miara dynamiki zjawisk prostych indywidualnych, tzn. służą do badania zmian w czasie jednego szeregu faktów.

• złożone (agregatowe, zespołowe) - są miara dynamiki zespołu zjawisk. Wyznaczane są dla określonej grupy badanej zbiorowości.

K. Romaniuk „Elementy ogólnej teorii statystyki”

B. Szulc „Statystyka dla ekonomistów”

S. Diamond „ Wszechstronna statystyka”

W. Starzyńska (red.), Podstawy statystyki, Difin, Warszawa 2004

A. Komosa, J. Musiałkiewicz, Statystyka, Ekonomik, Warszawa 1996

5

---