POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ ORGANIZACJI I ZARZADZANIA Katedra Podstaw Systemów Technicznych

Laboratorium z przedmiotu PODSTAWY METROLOGII

Ćwiczenie nr 2

Dokładność pomiarów, wyznaczanie błędów pomiarowych

Wykonali	Piotr Gola Marek Gaura
Kierunek	ZIP
Grupa	2
Sekcja	1
Data	30.01.2008

Rok akademicki 2008/2009

Semestr zimowy

1. Celem obu ćwiczeń było zapoznanie się z metodami wyznaczania błędów pomiarowych wielkości prostych i złożonych. W ćwiczeniu 1 należało wyznaczyć błędy względny i bezwzględny dla napięcia prądu stałego dokonanego dwoma różnymi miernikami aby zbadać poprawność dokonanych pomiarów. Natomiast w ćwiczeniu 2 należało wyznaczyć rezystancję żarówki metodą techniczną oraz obliczyć błąd wielkości złożonej korzystając z metody pochodnej logarytmicznej i różniczki zupełnej.

2. Do wykonania ćwiczenia użyliśmy dwóch mierników uniwersalnych typu:

1. MASTECH MY 67

2. DT 832

3. a) Wyniki pomiarów i obliczeń wynikających z przebiegu ćwiczeniu 1:

- Pomiar napięcia za pomocą miernika MASTECH MY 67 wynosił U_m = 3,661V na zakresie 4V co pozwoliło na wyznaczenie błędów bezwzględnego i względnego pomiarów.

Błąd bezwzględny:

ΔU_m= ± 0,5%W ± 2D

ΔU_m=

ΔU_m= 0,020305V

Błąd względny:

δU_M =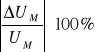
₌

- Pomiar napięcia za pomocą miernika DT832 wynosi U_D = 3,62V na zakresie 20V. Zatem wyznaczamy błędy względny i bezwzględny dokonanego pomiaru.

Błąd bezwzględny

ΔU_D = ±0,5%W ± 2D

ΔU_D =

ΔU_D = 0,0381V

Błąd względny:

δU_D =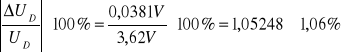

Tak, więc można stwierdzić, że oba pomiary różnią się wzajemnie z uwagi na różne zakresy, na których były dokonywane pomiary.

b) Wyniki pomiarów i obliczeń wynikających z przebiegu ćwiczenia 2:

Pomiar rezystancji metodą techniczną:

U = 5,96 V na zakresie 20V

I = 1,564 mA na zakresie 4mA

R_z = 3,776 kΩ

Błąd bezwzględny:

ΔR_z = ±0,8%W ± 1D

ΔR_z =

Błąd względny:

δR_z =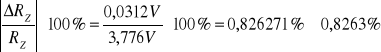

Rezystancję można obliczyć także stosując wzór prawa Ohma. Tak, więc:

R_W =

R_W =

Błąd bezwzględny:

ΔU = ±0,5%W ± 2D

ΔU =

ΔI = ±0,8%W ± 2D

ΔI =

ΔR_W =

ΔR_W =

Błąd bezwzględny:

δR_W =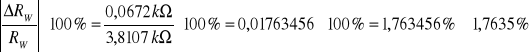

Metoda różniczki zupełnej

ΔR =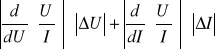

ΔR =

ΔR =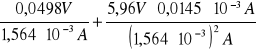
=

2

---