Sprawozdanie z ćwiczenia nr B-12

Michał Tomaniak Marcin Kmiecik	Zespół nr 22
Wydział Elektryczny	Ocena z przygotowania:
Czwartek 1115 - 1400	Ocena ze sprawdzenia:
Data: 4 maj, 1994	Zaliczenie:
Prowadzący: p. Ejchart	Podpis:

Temat: Badanie właściwości statystycznych elektronów emitowanych

z katody lampy próżniowej.

Podstawy teoretyczne.

1. Rozkład Maxwella dla gazu doskonałego.

Gaz doskonały jest to układ cząstek w którym można zaniedbać energię ich oddziaływania w porównaniu z ich energią kinetyczną, a same cząstki traktowane są jako punkty materialne. W takim układzie cząstki poruszają się ruchem jednostajnym prostoliniowym, zderzając się przy tym między sobą oraz ze ściankami naczynia w którym znajduje się gaz.

Rozpatrując układ makroskopowy w postaci gazu doskonałego wypełniającego naczynie i składającego się z bardzo dużej lecz skończonej liczby cząstek i zakładając, że gaz znajduje się w stanie stacjonarnym ( liczba cząstek w jednostce objętości, o danych prędkościach nie zależy od czasu).można stwierdzić, że średnia liczba cząstek o składowych prędkościach zawartych w przedziałach; vx,vx+dvx, vy,vy+dvy, vz,vz+dvz jest proporcjonalna do ogólnej liczby cząstek n(v)=n(vx,vy,,vz) znajdujących się w jednostce objętości i szerokości tego przedziału.

Funkcja n(v) nosi nazwę funkcji rozkładu prędkości cząstek. dla dużej liczby cząstek można przyjąć, że funkcja ta jest ciągła. Czyli:

,

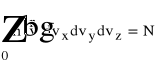
równanie to stanowi warunek normalizacji funkcji rozkładu prędkości n(v).

Z założonego warunku o stanie idealnego bezładu gazu wynika, że rozkład prędkości będzie izotropowy czyli taki, że funkcja rozkładu n(v) nie może zależeć od kierunku prędkości. Czyli funkcja ta powinna być funkcją argumentu:

co wyrażone we współrzędnych sferycznych można zapisać w postaci:

Z kolei traktując gaz jako idealny, czyli spełniający wszystkie warunki wymagane w kinetycznej teorii gazu, można zderzenia cząstek traktować jako całkowicie sprężyste. Ponadto zakładając że wszystkie cząstki mają taką samą masę m, to można zgodnie z zasadą zachowania energii napisać, że:

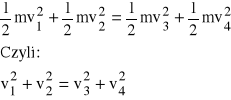
gdzie: v1,v2 - prędkości dwóch cząstek przed zderzeniem,

v3, v4 - prędkości dwóch cząstek po zderzeniu.

Powyższe równania przedstawiają warunki jakie powinna spełniać poszukiwana funkcja n(v).

Funkcją spełniającą te warunki jest funkcja postaci:

pozostaje jedynie wyznaczyć stałą B:

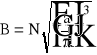
Po podstawieniu do wcześniejszego równania otrzymujemy ostateczną postać funkcji rozkładu n(v):

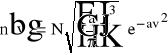
Mając rozkład prędkości cząstek można wyprowadzić funkcję rozkładu liczby cząstek według posiadanych przez nie energii kinetycznych:

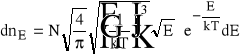
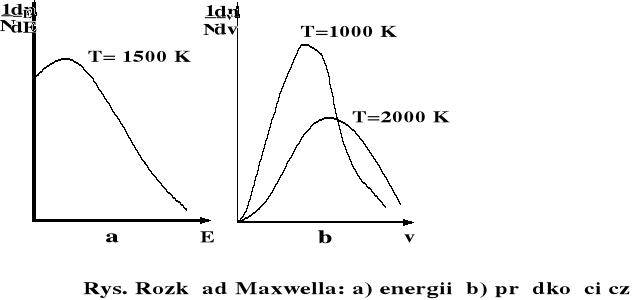
Powyższe funkcje rozkładu względnej liczby cząstek według posiadanych przez nie energii lub prędkości obrazuje poniższy rysunek:

Zjawisko termoemisji.

Termoemisją nazywamy emisję elektronów zachodzącą pod wpływem nagrzania metalu. W wysokich temperaturach pewna liczba elektronów w metalu znajduje się na wyższych poziomach energetycznych. Część tych elektronów pokonuje siły wiążące je z metalem i wydostaje się poza barierę potencjałów na zewnątrz. Emisję elektronów określa liczba elektronów emitowanych w jednostce czasu z jednostki powierzchni. liczba ta pomnożona przez ładunek elektryczny elektronu przedstawia prąd emisyjny na jednostkę powierzchni tzw. gęstość prądu emisyjnego która zależy od temperatury metalu i wyraża się wzorem:

gdzie: A - stała, - efektywna praca wyjścia z metalu, T - temperatura źródła elektronów.

natomiast średnia energia emitowanych elektronów wynosi:

gdzie: k - stała Boltzmanna, T - temperatura powierzchni emitującej .

Rozkład Maxwella dla elektronów termicznych.

Rozkład Maxwella obowiązujący dla gazu doskonałego można zastosować do opisu rozkładu elektronów termicznych emitowanych przez lampę elektronową dlatego, że koncentracja elektronów które opuściły metal jest o 10-15 rzędów mniejsza niż elektronów w metalu, co powoduje, że można zaniedbać odziaływanie między nimi upodabniając tym samym gaz elektronowy do gazu doskonałego.

W naszym wypadku źródłem elektronów termicznych jest katoda lampy próżniowej.

Elektrony opuszczając rozżarzoną katodę dzięki posiadanej energii kinetycznej docierają do anody powodując przepływ prądu anodowego. Energie kinetyczne poszczególnych elektronów są różne co potwierdza fakt, iż przykładając między anodę a katodę coraz większe napięcie hamujące liczba elektronów docierających do anody maleje. Docierają jedynie te elektrony których energia kinetyczna spełnia warunek:

Dla pewnej wartości Ua pole hamujące jest tak duże, że tylko nieliczne elektrony docierają do anody.

Liczba elektronów o energii większej od E=eUa , które przechodzą w jednostce czasu przez jednostkę powierzchni i osiągną anodę wyraża się wzorem:

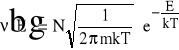
Natomiast prąd anodowy można zapisać jako:

Wykonanie ćwiczenia.

1. Łączymy układ pomiarowy wg dołączonej instrukcji.

2. Dla 4 różnych prądów żarzenia lampy elektronowej; w naszym przypadku:

- Iż = 0,58 A

- Iż = 0,59 A

- Iż = 0,60 A

- Iż = 0,50 A,

dokonujemy pomiarów prądu anodowego dla różnych wartości napięcia hamującego, które regulujemy za pomocą dzielnika napięcia. Wyniki notujemy w protokóle pomiarów.

3. Sporządzamy wykres zależności prądu anodowego w funkcji napięcia hamującego

( prąd anodowy na wykresie jest to ln(Ia/I0).

4. Z wykresu odczytujemy tangens kąta nachylenia prostej.

5. Wyznaczone tangensy kąta nachylenia prostej pozwalają nam wyznaczyć temperaturę

żarzenia katody. Korzystamy przy tym ze wzoru:

gdzie: k - stała Boltzmanna, e - ładunek elektronu.

Po podstawieniu i obliczeniu otrzymaliśmy następujące temperatury:

- dla Iż= 0,58 A T=1140 K

- dla Iż= 0,59 A T=1153 K

- dla Iż= 0,60 A T=1200 K

- dla Iż= 0,55 A T=1105 K

Dyskusja błędów.

Wyznaczone temperatury żarzenia katody obarczone są dość znacznymi błędami które wynikają z:

- klasy dokładności użytych mierników, błąd odczytanych wartości prądu anodowego i napięcia hamującego sięga w sumie około 5%

- Zastosowanej metody pomiarowej tzn. poprawnie mierzonego prądu anodowego. Skutkiem tego woltomierz wskazuje napięcie hamujące pomniejszone o spadek napięcia na amperomierzu, co wprowadza największe błędy do wyznaczonej później pośrednio temperatury żarzenia katody. Oczywiste jest że im większy prąd mierzy amperomierz tym większy spadek napięcia na jego ustroju pomiarowym i tym samym napięcie mierzone przez woltomierz sporo odbiega od rzeczywistej wartości. Dlatego też największymi błędami obarczona jest temperatura żarzenia katody T dla większych prądów żarzenia

i wynosi Twzgl 20%.

Najmniejszym błędem obarczona jest temperatura dla najmniejszego prądu żarzenia, co wynika z powyższych rozważań i wynosi Twzgl 10%

Poza wyżej wymienionymi źródłami błędów można wymienić jeszcze błędy wynikające ze:

stabilizacji prądu żarzenia lampy, jednak są one dużo mniejsze od wcześniej wymienionych.

Laboratorium z Fizyki.

Strona nr 5

---