Tomasz Michalski
Wyznaczanie współczynnika termicznej rozszerzalności liniowej metalu
W siatce krystalicznej ciała stałego każda drobina, atom lub jon, znajduje się w określonym położeniu równowagi, dookoła którego oscyluje. Drobiny w ciele stałym mogą przechodzić z miejsca na miejsce, jednakże takie przejścia zachodzą dosyć rzadko. Świadczą o tym niezmiernie powolny przebieg dyfuzji.
Wraz ze wzrostem temperatury ciała stałego wzajemne odległości między położeniami równowagi drobin wzrastają. W wyniku tego ma miejsce rozszerzalność cieplna ciał stałych.
Jeżeli weźmiemy pod uwagę ciało stałe określonego kształtu, to w miarę wzrostu temperatury rosną jego wymiary liniowe. W celu ujęcia zjawiska rozszerzalności liniowej przypuśćmy, że pręt, którego długość w temperaturze T0 wynosi l0 ogrzaliśmy do temperatury T, wskutek czego długość pręta wzrosła do lT. Zatem długość pręta wskutek jego ogrzania o ΔT = T - T0 wzrosła o Δl = lT - l0.
Przyrost długości pręta jest wprost proporcjonalny do przyrostu temperatury. Całkowita długość pręta podczas jego ogrzania o ΔT wzrośnie o
Δl = α l o ΔT,
A wartość każdej jednostki długości pręta ogrzanego o 1oC wzrośnie o
α =Δl/(l0*ΔT)
Wielkość α nazywamy współczynnikiem termicznym rozszerzalności liniowej. Jak widać, współczynnik rozszerzalności liniowej jest równy stosunkowi przyrostu długości do iloczynu pierwotnej długości i przyrostu temperatury.
Uwzględniając, że
Δl= lT- l0
Otrzymamy wzór na długość pręta w temperaturze T:
lT =l0 (1+ α ΔT).
Powyższa zależność stosuje się dokładnie tylko w niewielkim zakresie temperatur, stanowi bowiem pierwsze przybliżenie.
Dokładne pomiary wskazują, że należałoby stosować wyrażenie zawierające zależność długości również od kwadratu, a nawet i od sześcianu przyrostu temperatury, a więc typu:
lT = l0 (1+ α ΔT+ β ΔT2),
Przy czym współczynnik β jest na ogół znikomo mały i wywiera wpływ tylko przy stosunkowo dużych zmianach temperatury.
W miarę wzrostu temperatury wszystkie wymiary ciała rosną w tym samym stosunku, wobec tego rośnie też jego powierzchnia i objętość. W związku z tym można wprowadzić pojęcie współczynnika rozszerzalności powierzchniowej i objętościowej. Rozważmy przypadek ciała izotropowego.
Weźmy pod uwagę sześcian o krawędzi l0 w temperaturze T0 to po ogrzaniu do T długość każdej krawędzi wyniesie lT. Wobec tego w temperaturze T objętość VT sześcianu wyniesie:
VT = lT3 =l03 (1+α ΔT)3.
Z uwagi na małą wartość współczynnika α można zaniedbać wyrazy zawierające jego kwadrat i sześcian i w przybliżeniu przyjąć, że
VT =T0(1 +3 α ΔT)
Albo
VT =V0(1 + γ ΔT)
Gdzie
γ=3α
Jest współczynnikiem termicznym rozszerzalności objętościowej.
Przyrząd pozwalający na wyznaczenie współczynnika termicznej rozszerzalności
liniowej nazywamy dylatometrem. Stosowany w ćwiczeniu dylatometr przedstawia rysunek:
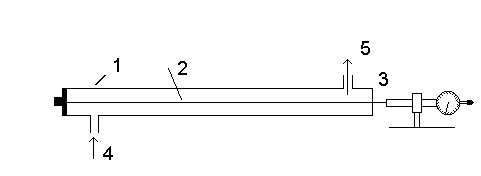
Posiada on płaszcz parowy 1, przez który przepuszcza się parę wodną w celu ogrzania badanego pręta. Czujnik zegarowy 3 pozwala ustalić wartość wydłużania pręta. Znajdujący się w płaszczu parowym pręt 2 podgrzewamy tak długo, aż temperatura płaszcza i pręta będzie równa temperaturze pary, nastąpi to wtedy, gdy ustanie ruch wskazówki czujnika wywołany wydłużeniem się pręta,
Kolejność czynności:
Zmierzyć długość pręta L0 i temperaturę początkową T0 .
Wstawić badany pręt między tylną ściankę płaszcza i główkę 3 trzpienia mierniczego czujnika. Odczytać wskazanie czujnika.
Przepuścić parę przez płaszcz parowy.
Odczytać ciśnienie barometryczne i z tablic- odpowiednią temperaturę wrzenia wody.
Odczytać położenie wskazówki czujnika i obliczyć LT - L0 pręta oraz ΔT (przyrost temperatury).
Obliczyć współczynnik rozszerzalności liniowej.
Wyszukiwarka
Podobne podstrony:
Wyznaczanie współczynnika rozszerzalności liniowej i objętościowej, Fizyka
Wyznaczanie współczynnika rozszerzalności liniowej metalu
Wyznaczanie współczynnika rozszerzalności liniowej i objętościowej, Fizyka
Wyznaczanie współczynnika rozszerzalności liniowej metalu
Wyznaczanie współczynnika lepkości cieczy metodą Ostwalda, Fizyka
20 wyznaczanie wspolczynnika zalamania swiatla refraktometrem abbego, fizyka lab
Wyznaczanie współczynnika lepkości dynamicznej metodą Stokes'a, Fizyka
Cw 11 - Wyznaczenie współczynnika rozszerzalności liniowej ciał stałych, Sprawozdania fizyka
Wyznaczanie współczynnika rozszerzalności liniowej metodą elektryczną, Pwr MBM, Fizyka, sprawozdania
Wyznaczanie współczynnika rozszerzalności liniowej i objętościowej ciał stałych, Fizyka
sprawozdanie 105 - Wyznaczanie współczynnika rozszerzalności liniowej ciał stałych, Fizyka
,Laboratorium podstaw fizyki, WYZNACZANIE WSPÓŁCZYNNIKA ROZSZERZALNOŚCI LINIOWEJ METODĄ
Wyznaczanie współczynnika rozszerzalności liniowej ciał stałych przy pomocy dylatometru 1 (2)
Wyznaczanie współczynnika rozszerzalności liniowej ciał stałych
Wyznaczanie współczynnika rozszerzalności liniowej metodą elektryczną 1 (2)
105 Wyznaczanie współczynnika rozszerzalności liniowej ciał stałych
więcej podobnych podstron