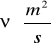Pracownia Zakładu Fizyki Technicznej Politechniki Lubelskiej
Nazwisko i imię Hanaj Daniel studenta:							Instytut i symbol grupy Ed 3.5
Data wykonania ćwiczenia: 96-12-04		Symbol ćwiczenia: 9.1	Temat zadania: Wyznaczanie współczynnika lepkości dynamicznej metodą Stokes'a
Zaliczenie:			Ocena:	Data:	Podpis

1.Tabela pomiarów:

Pomiar		2r [m]				t [s]			2R [m]			s [m]
1		0.001965				4.2			0.05135			0.500
2		0.001929				4.6			0.05130			0.499
3		0.001965				4.6			0.05135			0.500
4		0.001965				4.4
5		0.001965				4.6
6		0.001929				4.6
7		0.001965				4.4
8		0.001965				4.6
9		0.001929				4.6
10		0.001965				4.8
11		0.001929				4.6
12		0.001965				4.4
Ciecz
Olej Parafinowy	0,000977		0,02567	4.5	0,5			800		11340	296		0,18087	0,000226

2.Schemat wykonania ćwiczenia:

W celu wyznaczenia współczynnika lepkości cieczy stosuje się wiskozymetr Stokes'a. W ćwiczeniu mierzono czas opadania kulki t, drogi s, promienia kulki r, oraz promienia cylindra R.

Kulki użyte w doświadczeniu cechowała różnica średnic nie przekraczająca jednej działki okularu mikroskopu.

3.Część teoretyczna:

Zjawisko tarcia wewnętrznego zwanego lepkością związane jest z ruchem polegającym na przemieszczaniu się różnych części tego samego ciała względem siebie. Lepkość wykazują ciała we wszystkich stanach skupienia, chociaż niektóre z nich w bardzo niskich tempera-turach przechodzą w stan nadpłynności, w którym ich lepkość równa jest zeru.

Lepkością nazywa się właściwość ciał polegającą na występowaniu sił oporu, wywoływanych siłami zewnętrznymi, powodującymi odkształcenia ciał stałych, a płynięcie cieczy i gazów. Przy analizie płynów odstępuje się od ich budowy cząsteczkowej, traktując je jako ośrodki ciągłe tzn. Rozmieszczone w sposób ciągły w zajmowanej przez nie przestrzeni. Przy takim podejściu wykorzystuje się najczęściej metodę Eulera, która podaje zależność wektora prędkości przepływu płynu od współrzędnych przestrzennych i czasu:

.

Ciecze traktować możemy jako substancję lepką i nieściśliwą. Przepływ jej może mieć charakter laminarny - warstwowy. Siły oporu występujące w trakcie przepływu cieczy przy przesuwaniu się jednych warstw względem drugich powodują, że warstwa poruszająca się szybciej działa siłą przyspieszającą na warstwę poruszającą się wolniej i odwrotnie.

Wartość siły tarcia wewnętrznego dla przepływu laminarnego podaje wzór Newtona:

gdzie  jest współczynnikiem lepkości dynamicznej, jest zmianą prędkości ruchu warstw na jednostkę długości w kierunku wewnętrznej normalnej do powierzchni warstwy. Wynika z tego więc, że współczynnik lepkości dynamicznej jest równy liczbowo sile statycznej jaka powinna działać na powierzchnię 1m² warstwy cieczy o grubości 1m, aby górna powierzchnia tej warstwy poruszała się z prędkością o 1 m/s większą niż dolna.

Jednostką współczynnika tarcia wewnętrznego jest niutonosekunda na metr kwadratowy:

.

Często używa się również współczynnika lepkości kinematycznej  Oblicza się go jako stosunek współczynnika lepkości dynamicznej do gęstości cieczy .

.

Współczynnik lepkości dynamicznej zależy od rodzaju cieczy, temperatury i ciśnienia. Jego wartość określa wzór:

gdzie E_a jest energią aktywacji przepływu lepkiego, k - stałą Boltzmana, T - temperatura w skali Kelvina.

Na ciało poruszające się w cieczy lepkiej działają siły oporu. Jeżeli poruszające się ciało ma kształt opływowy i porusza się z dostatecznie małą prędkością, siła oporu wywołana jest lepkością cieczy. Warstewka cieczy bezpośrednio przylegająca do ciała porusza się razem z tym ciałem. Prowadzi to do przesuwania się warstw cieczy względem siebie, co jest bezpośrednią przyczyną występowania siły tarcia wewnętrznego. Siła ta powoduje hamowanie najszybszych warstw cieczy, a więc i warstwy przylegającej do ciała tzn. I samego ciała.

Zgodnie z prawem Stokes'a działająca wtedy siła oporu jest wprostproporcjonalna do prędkości, współczynnika lepkości dynamicznej i liniowych rozmiarów ciała. Jeżeli tym ciałem jest kula o promieniu r, która porusza się w cieczy o współczynniku ruchem jednostajnym z prędkością V, to zgodnie z tym prawem działa na nie siła oporu wyrażona wzorem:

.

Drugi mechanizm powstawania siły oporu w cieczy lepkiej związany jest z powstawaniem wirów. W takim przypadku część pracy zostaje zużyta na powstanie wirów. Energia wirów w wyniku lepkości przechodzi w energię wewnętrzną płynu, a to pociąga za sobą szybki wzrost siły oporu.

Dla kulki poruszającej się w cylindrze o promieniu R w cieczy o gęstości ρ_c, współczynniku lepkości  Parametry kulki: r - promień, ρ_k.

Wartość współczynnika lepkości dynamicznej przyjmuje postać:

.

Prędkość kulek powinna być mała, aby nie tworzyły się wiry. Można to uzyskać, jeżeli promień kulki jest mały, a ich gęstość niewiele różni się od gęstości cieczy.

4. Opracowanie wyników pomiaru:

Obliczanie błędu względnego maksymalnego lepkości dynamicznej:

Pomiar lepkości dynamicznej był pomiarem pośrednim - poprzez pomiar r, R, s, t.

Błąd względny maksymalny wynosi więc:

Obliczanie błędu względnego maksymalnego pomiaru lepkości dynamicznej dla pomiaru

najbardziej zbliżonego do średniej :

Metoda Gaussa:

Lp.
1	0.000982	4.2		0.000006	-0.3	0.000040	0.09
2	0.000964	4.6		-0.000012	0.1	0.000134	0.01
3	0.000982	4.6		0.000006	0.1	0.000040	0.01
4	0.000982	4.4		0.000006	-0.1	0.000040	0.01
5	0.000982	4.6		0.000006	0.1	0.000040	0.01
6	0.000964	4.6		-0.000012	0.1	0.000134	0.01
7	0.000982	4.4		0.000006	-0.1	0.000040	0.01
8	0.000982	4.6		0.000006	0.1	0.000040	0.01
9	0.000964	4.6		-0.000012	0.1	0.000134	0.01
10	0.000982	4.8		0.000006	0.3	0.000040	0.09
11	0.000964	4.6		-0.000012	0.1	0.000134	0.01
12	0.000982	4.4		0.000006	-0.1	0.000040	0.01

Średni błąd kwadratowy pojedynczego pomiaru:

Średni błąd kwadratowy średniej:

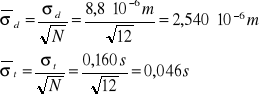
Średni błąd kwadratowy pomiaru współczynnika lepkości dynamicznej:

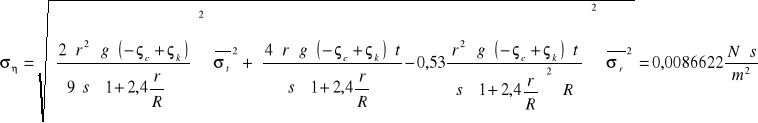
Otrzymany wynik napięcia powierzchniowego wyznaczony z prawdopodobieństwem 68,3%.

Otrzymany wynik napięcia powierzchniowego wyznaczony z prawdopodobieństwem 99,7%.

---