Pd am2.5 18.03.2010

Zad.1 Wyznaczyć dziedzinę funkcji oraz jej ilustrację graficzną

a)
b)

Zad.2 Wyznaczyć warstwice funkcji f, a następnie najmniejszą i największą wartość tej funkcji na podanym zbiorze A

a)

b)

zad.3

Naszkicować wykresy funkcji

a)
, b)
, c)

zad.4

Obliczyć granice

a)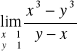
b)
, c)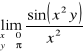

Zad.5

Wykazać, że nie istnieją granice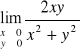
,
.

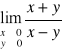
Zad.6

Obliczyć z definicji pochodne cząstkowe funkcji rzędu pierwszego we wskazanym punkcie

a)

b)

Zad.7

Korzystając z reguł różniczkowania obliczyć wszystkie pochodne cząstkowe funkcji rzędu drugiego

a)
b)

odpowiedzi

zad.1

a) dwa sektory kątowe
oraz
bez punktu

b)

oktant (ósemka
)

zad.2

a) największa wartość funkcji na zbiorze A wynosi
, najmniejsza
.

Warstwicami są linie proste
gdzie c dowolna liczba rzeczywista.

b)
dla
największa wartość funkcji na zbiorze A wynosi
, najmniejsza
.

Zad.4 a)
; b)
; c)

zad. 6 a)

b)

zad.7

a)

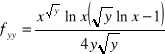
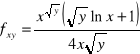
b)

---