i - jednostka urojona
![]()
Wprowadzamy liczby zespolone z mające postać sumy
![]()
Gdzie a i b są liczbami rzeczywistymi. Część rzeczywistą liczby zespolonej z oznacza się symbolem Re z, a część urojoną - symbolem Im z, zatem
Re z=a, Im z=b
Liczbę zespoloną różniącą się od liczby z=a+Bi tylko znakiem współczynnika przy i nazywamy liczbą sprzężoną z liczbą z i oznaczamy przez ![]()
:
![]()
![]()
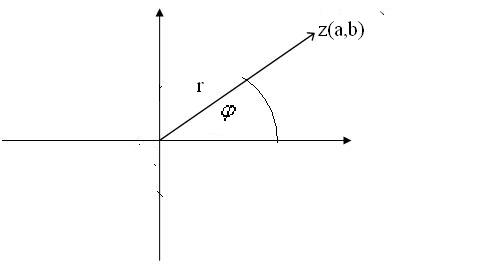
Liczbę zespoloną a+bi sprowadzamy do postaci trygonometrycznej
![]()
![]()
gdzie liczba dodatnia r jest modułem, a ![]()
- argumentem danej liczby zespolonej.
![]()
![]()
![]()
Aby podnieść liczbę zespoloną do potęgi naturalnej, posługujemy się tzw. wzorem Moivre'a:
![]()
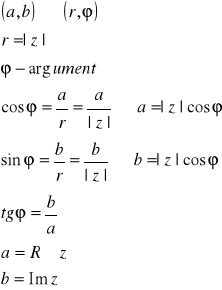
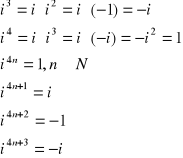
TEORIA GAUSSA
![]()
Działania na liczbach zespolonych:
![]()
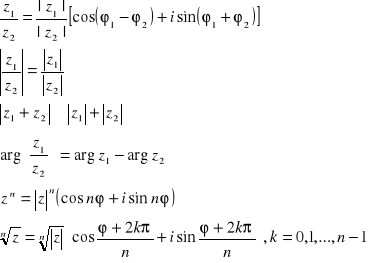
Dodawanie, odejmowanie i mnożenie liczb zespolonych w postaci algebraicznej wykonuje się tak samo jak odpowiednie operacje na wyrażeniach algebraicznych; należy tylko pamiętać o równości i2 = − 1:
Aby podzielić przez siebie dwie liczby zespolone, wystarczy pomnożyć dzielną i dzielnik przez liczbę sprzężoną do dzielnika (analogicznie do usuwania niewymierności z mianownika w wyrażeniach algebraicznych)
Liczby zespolone
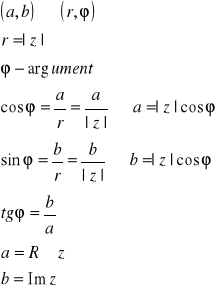
![]()
Wyszukiwarka
Podobne podstrony:
Liczby zespolon1, Matematyka
Matematyka (rok I i II), Zespolone, Liczby zespolone:
liczby zespolone zadania, Matematyka
Matematyka - Liczby zespolone i Szeregi liczbowe, AM SZCZECIN, MATEMATYKA, Matematyka
Matematyka - pochodne + całki + liczby zespolone, STUDIA
liczby zespolone teoria, Matematyka
Matematyka III (Ćw) Lista 01 Liczby zespolone Odpowiedzi
Matematyka (rok I i II), ZESPOLKI, Liczby zespolone:
Matematyka (rok I i II), SCIAGA, Liczby zespolone:
ZAdania z matematyki, LICZBY ZESPOLONE 2010, LICZBY ZESPOLONE - ZADANIA
2 Matematyka liczby zespolone
F 13 Liczby zespolone
liczby zespolone 6 id 267992 Nieznany
więcej podobnych podstron