Część teoretyczna

Ogniwo galwaniczne stanowi układ zbudowany z dwóch półogniw, który może wykonać pracę elektryczną kosztem zmiany energii zachodzącej w układzie w wyniku przemian chemicznych lub zmian stężenia. Półogniwa (elektrody) stanowią najczęściej fazy metaliczne, zanurzone w przewodniku jonowym.

W ogniwie galwanicznym obydwa półogniwa graniczą ze sobą w taki sposób, że po połączeniu przewodnikiem na zewnątrz ogniwa możliwa jest wędrówka ładunku elektrycznego od jednej elektrody do drugiej. W czasie przepływu prąd na elektrodzie dodatniej (katodzie)przebiega reakcja redukcji:

(1)

A na elektrodzie ujemnej (anodzie) - reakcja utleniania :

(2)

Elektrony płyną od anody do katody. Proces wypadkowy tych reakcji składowych przedstawia reakcję zachodzącą w ogniwie :

(3)

Dla każdego ogniwa charakterystyczna jest wielkość różnicy potencjałów pomiędzy dwoma jednakowymi przewodnikami metalicznymi dołączonymi do elektrod, gdy przez ogniwo nie przepływa prąd elektryczny. Zostaje wtedy osiągnięty stan równowagi reakcji elektrodowych w obu półogniwach. Taka równowagowa różnica potencjałów jest definiowana jako napięcie ogniwa w warunkach bezprądowych lub siła elektromotoryczna ogniwa E.

Badanie reakcji chemicznej w ogniwie ma szczególne znaczenie ze względu na możliwość przeprowadzenia w nim procesu w sposób odwracalny. W warunkach izotermicznychno-izobarycznych praca elektryczna, której dostarcza ogniwo, równa jest potencjałowi termodynamicznemu ΔG reakcji zachodzącej w ogniwie :

(4)

Gdzie: n - liczba moli elektronów biorących udział w pracy ogniwa, F - stała Faradaya, E - siła elektromotoryczna ogniwa.

Jeżeli w układzie przebiega reakcja:

(5)

To towarzysząca jej zmiana potencjału termodynamicznego ΔG określona jest równaniem:

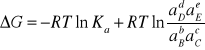
(6)

Gdzie: K_a - stała równowagi reakcji, a_D,a_E....- aktywności reagentów, R - stała gazowa, T - temperatura reakcji

Łącząc równania (4) i (6) otrzymujemy:

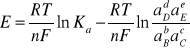
(7)

Siłę elektromotoryczną ogniwa, w którym aktywności wszystkich reagujących substancji są równe jedności, nazywa się standardową siłą elektromotoryczną i oznacza symbolem E°. Jej wartość zależy od ogniwa i jest stała w danej temperaturze.

Z równania (7) wynika:

(8)

A więc

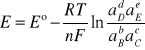
(9)

Zależność określającą związek siły elektromotorycznej ogniwa z aktywnością reagentów, zwaną równaniem Nernsta, można zastosować do obliczania potencjału pojedynczej elektrody, na której zachodzi reakcja utleniania bądź redukcji.

Różniczkując równanie (4) względem temperatury ( pod stałym ciśniniem) otrzymujemy:

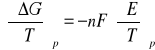
(10)

Porównując otrzymaną pochodną z zależnością wynikająca z II zasady termodynamiki:

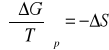
(11)

Otrzymuje się wyrażenie na entropię ΔS reakcji zachodzącej w ogniwie:

(12)

Na podstawie równań (4) i (12) oraz ogólnej zależności termodynamicznej:

(13)

Można obliczyć entalpię ΔH rteakcji elektrochemicznej ogniwa:

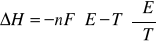
(14)

Zatem, pomiar siły elektromotorycznej ogniwa i jej zależności od temperatury umożliwia wyznaczenie funkcji termodynamicznych ΔH, ΔS i ΔG reakcji zachodzącej w ogniwie.

W badanym ogniwie:

Nie występuje potencjał dyfuzyjny, ponieważ nasycony roztwór KCl jest elektrolitem wspólnym dla obu elektrod.

Na elektrodzie kalomelowej (katodzie) zachodzi reakcja redukcji:

Natomiast na elektrodzie chlorosrebrowej (anodzie) - utleniania

Sumaryczną reakcję zachodzącą w tym ogniwie można przedstawić za pomocą równania:

Część obliczeniowa

Wyznaczam metodą najmniejszych kwadratów współczynnik kierunkowy
prostej E=f(T)

Wyznaczam metodą graficzną współczynnik kierunkowy
prostej E=f(T)

Obliczam entropię ΔS reakcji przebiegającej w ogniwie w temperaturze 298 K wykorzystując do obliczeń współczynnik
obliczony metodą najmniejszych kwadratów z równania:

Obliczam entalpię ΔH reakcji przebiegającej w ogniwie w temperaturze 298 K wykorzystując do obliczeń współczynnik
obliczony metodą najmniejszych kwadratów z równania:

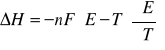
Obliczam potencjał termodynamiczny ΔG reakcji przebiegającej w ogniwie w temperaturze 298 K wykorzystując do obliczeń współczynnik
obliczony metodą najmniejszych kwadratów z równania:

---