M-01. Równia pochyła
1. Cel eksperymentu
Wyznaczenie rozkładu przyspieszenia wózka zjeżdżającego po równi pochyłej, dla różnych wartości kąta nachylenia bieżni względem poziomu.
2. Wiadomości teoretyczne
W celu obliczenia przyspieszenia masy Mw zsuwającej się po płaszczyźnie nachylonej do poziomu pod kątem α, to musimy uwzględniać trzy siły działające na ciało:
Siła ciężkości Mw g skierowana w dół;
Siła nacisku N = Mw cosα ciała na płaszczyznę skierowana w dół pod kątem α do pionu;
Siła tarcia T przeciwstawiająca się ruchowi ciała w dół po równi.
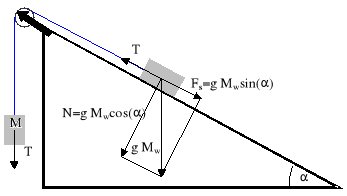
Rozkładając siłę Mw⋅g na kierunki prostopadły i równoległy do równi możemy wyznaczyć siłę nacisku N ciała na równię oraz siłę ściągającą Fs. Składowa N jest niezbędna do określenia wielkości siły tarcia, jeśli znany jest współczynnik tarcia μk. Trzy siły, dodane wektorowo, wskazują siłę wypadkową Fwyp która powoduje ruch ze stałym przyśpieszeniem a:
![]()
, ![]()
.
Jeżeli ciało porusza się po równi pochyłej bez tarcia (praktycznie rzecz biorąc można to zrealizować w przypadku toczenia się ciała - wózka) to przyspieszenie ciała zależy tylko od kąta nachylenia równi:
![]()
.
W przypadku niniejszego ćwiczenia, gdy siła tarcia T jest siłą naciągu linki można otrzymać:
![]()
,
gdzie: Mw, M, m - masy wózka, obciążnika, bloczka[20 g]; α - kąt nachylenia bieżni równi pochyłej do poziomu i przyspieszenie ziemskie g = 9.81 m/s2
3. Opis aparatury pomiarowej
Do eksperymentów wykorzystano stanowisko COBRABID zawierające komputer z oprogramowaniem pomiarowym, interfejs pomiarowy, bloczek z otworami zespolony z foto-bramką, uchwyt mocujący bloczek, ocechowane obciążniki z wieszakami i nić.
4. Przebieg ćwiczenia.
Po uruchomieniu programu „Fizyka”, Po wybraniu z menu opcji 4 i potwierdzeniu klawiszem Enter, wyświetlane są parametry istotne dla tego doświadczenia w następującej formie:
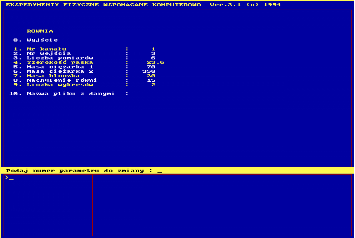
W pozycjach 5 i 6 wpisać masy ciężarka M i wózka Mw a w pozycji 8 kąt nachylenia równi α. Potwierdzenie, że dokonano już wszystkich zmian przez wciśnięcie klawisza `0', a następnie `Enter', co powoduje pojawienie się napisu „wciśnij dowolny klawisz”. Po naciśnięciu dowolnego klawisza należy zwolnić wózek, aby zaczął się staczać po równi. Przed puszczeniem wózka sprawdzić czy nie ma zbyt dużych wahań ciężarka hamującego, ponieważ mogłoby to znacznie obniżyć dokładność pomiarów. Pozycja startowa wózka powinna znajdować w okolicach połowy długości równi.
5. Pomiary przyspieszenia wózka w funkcji kąta nachylenia równi przy stałych wartościach Mw i M
Dla zadanych przez prowadzącego wartości mas wózka Mw i ciężarka M znaleźć minimalną wartość kąta nachylenia równi, przy której jeszcze występuje zjeżdżanie.
Masa wózka: Mw [g] = |
||||||||||
Masa ciężarka: M [g] = |
||||||||||
α [deg] |
|
|
|
|
|
|
|
|
|
|
sinα |
|
|
|
|
|
|
|
|
|
|
a [m/s2] |
|
|
|
|
|
|
|
|
|
|
Δa [m/s2] |
|
|
|
|
|
|
|
|
|
|
Następnie należy wykonać pomiary przyspieszenia wózka a i błędu pomiaru przyspieszenia Δa, dla różnych wartości kąta nachylenia bieżni względem poziomu. Wartość kąta nachylenia równi należy dobrać w zakresie między αmin a około 50°. Model równi pochyłej ma możliwość stałego nastawu kątów nachylenia o wartościach (kolejne otwory od lewej): 5, 10, 15, 20 i 250. Należy przy tym zmierzyć (obliczyć) właściwy kąt nachylenia z powodu możliwego rozkalibrowania zastawów pierwotnych.
6. Pomiary przyspieszenia wózka przy różnych wartościach Mw i M i przy stałym kącie nachylenia równi
Dla zadanej przez prowadzącego wartości kąta nachylenia równi α i masy wózka Mw wyznaczyć wartość maksymalną masy obciążnika, przy której występuje jeszcze zjeżdżanie wózka. Mmax=.......................[g]
Następnie należy wykonać pomiary przyspieszenia a i błędu pomiaru przyspieszenia Δa wózka dla różnych wartości mas ciężarka i przy stałej wartości kąta α nachylenia równi. Masy ciężarka należy dobrać w zakresie od 10g do Mmax.
Kąt nachylenia równi: α [deg] = |
||||||||||
Masa wózka: Mw [g] = |
||||||||||
M [g] |
|
|
|
|
|
|
|
|
|
|
a [m/s2] |
|
|
|
|
|
|
|
|
|
|
a(Mw+M+0,5m) [kg⋅m/s2] |
|
|
|
|
|
|
|
|
|
|
Δa [m/s2] |
|
|
|
|
|
|
|
|
|
|
7. Prezentacja wyników eksperymentu
Wyniki pomiarów przyspieszenia doświadczalnego, adoś, zebrane w tablicach, należy przedstawić graficznie w postaci punktów na wykresach Y = f(X):
1) a = f1(sinα); 2) a(Mw+M+0,5m) = f2(M). Obliczyć niepewność względną Δa/a.
Na powyższe wykresy nanieść także odpowiednie zależności teoretyczne, Y = f(X), obliczone dla zadanych parametrów pomiaru, Mw, M, α i m.
Porównać odchylenie przyspieszenia doświadczalnego, adoś, od teoretycznego, ateor, (adoś - ateor), z niepewnością standardową Δa i podać objaśnienia ewentualnej rozbieżności wartości (adoś - ateor) i Δa, korzystając z podstaw pomiarów niepewności i w pracowni fizycznej.
8. Wnioski
Protokół pomiarowy
Ćw. M-01. |
Laboratorium z fizyki |
||
Rok akadem:
|
Temat: Równia pochyła |
||
Kierunek:
Grupa: |
Imię i Nazwisko:
|
||
|
Ocena |
Data Zaliczenia |
Podpis |
L |
|
|
|
S |
|
|
|
K |
|
|
|
Masa wózka: Mw [g] = |
||||||||||
Masa ciężarka: M [g] = |
||||||||||
α [deg] |
|
|
|
|
|
|
|
|
|
|
sinα |
|
|
|
|
|
|
|
|
|
|
a [m/s2] |
|
|
|
|
|
|
|
|
|
|
Δa [m/s2] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rys. 1. Wykres zależności a w funkcji sinα.
Kąt nachylenia równi: α [deg]= |
||||||||||
Masa wózka: Mw [g]= |
||||||||||
M [g] |
|
|
|
|
|
|
|
|
|
|
a [ms2] |
|
|
|
|
|
|
|
|
|
|
a(Mw+M+0,5m) [kg⋅m/s2] |
|
|
|
|
|
|
|
|
|
|
Δa [m/s2] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rys. 2. Wykres zależności a(Mw+M+0,5m) w funkcji M.
Pomiar okresu drgań wahadła prostego
Cel eksperymentu
Sprawdzić charakter teoretycznej zależności okresu drgań wahadła prostego T od jego długości l i wyznaczyć przyspieszenie ziemskie g.
Wiadomości teoretyczne
Wahadło fizyczne może być traktowane jako wahadło proste, jeżeli cała masa ciężarka m jest skoncentrowana na końcu nierozciągliwej nici o długości l. Moment bezwładności I może być obliczony w tym przypadku jako: ![]()
. Okres drgań wahadła prostego:
![]()
zależy od długości nici l i od przyspieszenia ziemskiego g. Podany wzór na okres drgań jest poprawny dla małych wychyleń θ, co odpowiada warunkowi: sinθ = θ.
Opis aparatury pomiarowej
Do eksperymentów wykorzystane jest stanowisko firmy COBRABID zawierające komputer z oprogramowaniem pomiarowym, interfejs pomiarowy, fotobramkę, stojak, ramię, obciążnik wahadła i nić.
W trakcie jednego okresu drgań, obciążnik wahadła wchodzi dwukrotnie w przestrzeń pomiarową fotobramki przesłaniając fototranzystor (stan wysoki). Okres drgań wahadła może być wyznaczony jako suma czasów, w których fototranzystor znajduje się dwukrotnie w stanie niskim i dwukrotnie w stanie wysokim. Czasy te są w trakcie eksperymentu precyzyjnie mierzone i zapamiętywane w pamięci interfejsu pomiarowego. Jako wynik użytkownik otrzymuje wartość średnią okresu drgań wahadła zmierzoną dla kilku okresów drgań wahadła.
Przebieg ćwiczenia
Po uruchomieniu programu „Fizyka”, wybraniu z menu opcji 2 i potwierdzeniu wyboru klawiszem Enter, wyświetlane są parametry istotne dla tego doświadczenia w formie następującej:
W pozycji 3 wpisać liczbę pomiarów (od 6 do 12) a w pozycji 4 długość wahadła. Po ustawieniu parametrów eksperymentu wcisnąć klawisz '0', a następnie `Enter', co powoduje pojawienie się napisu „wciśnij dowolny klawisz”. Należy obecnie wprawić w ruch wahadło, odchylając jego obciążnik o niewielki kąt od pionu, i po kilku wahnięciach wcisnąć dowolny klawisz w celu uruchomienia rejestracji pomiaru.
Należy wykonać pomiary okresu drgań wahadła prostego T dla różnych długości nici l a jednej masy wahadła.
Masa ciężarka: m [g] = |
||||||||||
l [m] |
|
|
|
|
|
|
|
|
|
|
T [s] |
|
|
|
|
|
|
|
|
|
|
ΔT [s] |
|
|
|
|
|
|
|
|
|
|
T2 [s] |
|
|
|
|
|
|
|
|
|
|
Gdzie: ΔT [s]-jest niedokładnością wyznaczenia okresu odczytanym z ekranu monitora.
Prezentacja wyników eksperymentu
Wyniki pomiarów okresu drgań, T, zebrane w tablicach wraz z jego błędami należy przedstawić graficznie w postaci punktów na wykresie, Y = f(X) → T2 = f(l).
Na powyższy wykres należy nanieść także odpowiednią zależność teoretyczną, Y = f(X), obliczoną dla zadanych parametrów pomiaru, l i g.
Porównać odchylenie doświadczalnego, Tdoś, i teoretycznego, Tteor, okresów, (Tdoś - Tteor), z niedokładnością standardową ΔT i podać objaśnienia ewentualnej rozbieżności wartości (Tdoś - Tteor) i ΔT, korzystając z podstaw pomiarów niedokładności w pracowni fizycznej.
Wnioski
Protokół pomiarowy
Ćw. M-02. |
Laboratorium z fizyki |
||
Rok alkadem.:
|
Temat: Pomiar okresu drgań wahadła prostego |
||
Kierunek:
Grupa: |
Imię i Nazwisko:
|
||
|
Ocena |
Data Zaliczenia |
Podpis |
L |
|
|
|
S |
|
|
|
K |
|
|
|
Wyniki pomiarów okresu drgań wahadła prostego w funkcji długości wahadła l.
Masa ciężarka: m[g]= |
||||||||||
l [m] |
|
|
|
|
|
|
|
|
|
|
T [s] |
|
|
|
|
|
|
|
|
|
|
ΔT [s] |
|
|
|
|
|
|
|
|
|
|
T2 [s] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rys. 1. Wykres zależności T2 w funkcji l.
6
Laboratorium Fizyki. Równia pochyła. Wahadło.
1
Katedra Podstaw Elektroniki, WEiI PK. Koszalin 2009.
Wyszukiwarka
Podobne podstrony:
InstrukcjeĆw.2009 2010, Cw.1.E-01. Badanie właściwości elektrycznych kondensatora płaskiego, Laborat
LKM cw 01 02
tope cw6 gr3, [ WEEKENDOWE ], 2009-2010 semestr 01 (zimowy)
cw 01 02
LKM cw 01 02
2010 01 02, str 106 110
9fizyka rownia pochyla cw 18, Uczelnia, sem I, fiza, LABORATORIUM, laborki
02 poznawcza reprezentacje 2009 2010 st2
2010 01 02, str 100 105
2010 01 02, str 083 086
2010 01 02, str 053
ćw 28 02 2010
ćwiczenia, Praca domowa ćw 2, Chemia ćwiczenia, I rok IŚ, studia stacjonarne 2009/2010
2010 01 02, str 154 157
2010 01 02, str 077 080
2010 01 02, str 122 126
Informatyka w administracji 01 2009 2010
więcej podobnych podstron