POLITECHNIKA LUBELSKA W LUBLINIE |
Laboratorium Podstaw Elektrotechniki I Ćwiczenie nr 5 |
||||
Nazwisko: |
Imię : |
Semestr : II |
Grupa : ED 2.7 |
Rok akademicki : 1996/97 |
|
Temat ćwiczenia : Obwody magnetyczne |
Data wykonania: 24-03-1990 |
Ocena : |
|||
1. Wyznaczenie i obserwacja dynamicznej charakterystyki magnesowania
Rys. 1.1. Schemat układu do oscylografowania pętli histerezy.
Tabela 1.2
Przekrój czynny rdzenia |
SFe = 13 cm2 |
Średnia długość linii strumienia w rdzeniu |
lśr = 44 cm |
Rezystancja opornika pomiarowego |
R1 = 8 W |
Liczba zwojów uzwojenia wzbudzającego pomiarowego |
z1 = 1100 z1 = 130 |
Parametry układu całkującego |
R2 = 11 kW C2 = 2 mF |
Czułość wejścia „X” oscyloskopu Czułość wejścia „Y” oscyloskopu |
Sx = 1 cm/V Sy = 0,5 cm/V |
Na podstawie zaobserwowanej charakterystyki magnesowania dokonano następujących odczytów:
Obliczenia:
2. Badanie nierozgałęzionego obwodu magnetycznego. Wyznaczanie charakterystyki magnesowania prądem przemiennym.
Rys. 2.1. Schemat połączeń układu do wyznaczania charakterystyki magnesowania.
Tabela 2.2
Z1 |
Zp |
l |
SFe |
- |
- |
m |
cm2 |
600 |
1100 |
0,34 |
11 |
Tabela 2.3
Pomiary |
Obliczenia |
||||||||
|
U1 |
I1 |
Up |
ka |
Qm |
Hm |
F |
Bm |
|
Lp |
V |
A |
V |
- |
A |
A/m. |
mWb |
T |
|
|
d = 0 |
||||||||
1 |
20 |
0,00 |
40 |
1,41 |
0,00 |
0,00 |
0,16 |
0,15 |
|
2 |
30 |
0,05 |
55 |
1,41 |
42,30 |
124,41 |
0,23 |
0,20 |
|
3 |
40 |
0,06 |
75 |
1,41 |
50,76 |
149,29 |
0,31 |
0,28 |
|
4 |
50 |
0,07 |
93 |
1,41 |
59,22 |
174,18 |
0,38 |
0,35 |
|
5 |
60 |
0,09 |
110 |
1,41 |
76,14 |
223,94 |
0,45 |
0,41 |
|
6 |
70 |
0,10 |
128 |
1,41 |
84,60 |
248,82 |
0,52 |
0,48 |
|
7 |
80 |
0,12 |
147 |
1,41 |
101,52 |
298,59 |
0,60 |
0,55 |
|
8 |
90 |
0,14 |
165 |
1,42 |
119,28 |
350,82 |
0,68 |
0,61 |
|
9 |
100 |
0,15 |
183 |
1,42 |
127,80 |
375,88 |
0,75 |
0,68 |
|
10 |
110 |
0,17 |
200 |
1,42 |
144,84 |
426,00 |
0,82 |
0,74 |
|
11 |
120 |
0,18 |
217 |
1,42 |
153,36 |
451,06 |
0,89 |
0,81 |
|
12 |
130 |
0,20 |
235 |
1,43 |
171,60 |
504,71 |
0,96 |
0,87 |
|
d = 0,3 |
|||||||||
1 |
20 |
0,09 |
38 |
1,41 |
76,14 |
223,94 |
0,16 |
0,14 |
|
2 |
30 |
0,12 |
53 |
1,41 |
101,52 |
298,59 |
0,22 |
0,20 |
|
3 |
40 |
0,16 |
90 |
1,41 |
135,36 |
398,12 |
0,37 |
0,34 |
|
4 |
50 |
0,21 |
87 |
1,41 |
177,66 |
522,53 |
0,36 |
0,32 |
|
5 |
60 |
0,24 |
103 |
1,41 |
203,04 |
597,18 |
0,42 |
0,38 |
|
6 |
70 |
0,28 |
120 |
1,41 |
236,88 |
696,71 |
0,49 |
0,45 |
|
7 |
80 |
0,32 |
137 |
1,41 |
270,72 |
796,24 |
0,56 |
0,51 |
|
8 |
90 |
0,37 |
155 |
1,41 |
313,02 |
920,65 |
0,63 |
0,58 |
|
9 |
100 |
0,41 |
170 |
1,41 |
346,86 |
1020,18 |
0,70 |
0,63 |
|
10 |
110 |
0,45 |
187 |
1,41 |
380,70 |
1119,71 |
0,77 |
0,70 |
|
11 |
120 |
0,49 |
205 |
1,41 |
414,54 |
1219,24 |
0,84 |
0,76 |
|
12 |
130 |
0,53 |
222 |
1,41 |
448,38 |
1318,76 |
0,91 |
0,83 |
|
d = 0,7 |
|||||||||
1 |
20 |
0,14 |
35 |
1,41 |
118,44 |
348,35 |
0,14 |
0,13 |
|
2 |
30 |
0,19 |
50 |
1,41 |
160,74 |
472,76 |
0,20 |
0,19 |
|
3 |
40 |
0,25 |
65 |
1,41 |
211,50 |
622,06 |
0,27 |
0,24 |
|
4 |
50 |
0,32 |
83 |
1,41 |
270,72 |
796,24 |
0,34 |
0,31 |
|
5 |
60 |
0,38 |
97 |
1,41 |
321,48 |
945,53 |
0,40 |
0,36 |
|
6 |
70 |
0,45 |
113 |
1,41 |
380,70 |
1119,71 |
0,46 |
0,42 |
|
7 |
80 |
0,52 |
130 |
1,41 |
439,92 |
1293,88 |
0,53 |
0,48 |
|
8 |
90 |
0,58 |
147 |
1,41 |
490,68 |
1443,18 |
0,60 |
0,55 |
|
9 |
100 |
0,64 |
162 |
1,41 |
541,44 |
1592,47 |
0,66 |
0,60 |
|
10 |
110 |
0,70 |
178 |
1,41 |
592,20 |
1741,76 |
0,73 |
0,66 |
|
11 |
120 |
0,77 |
195 |
1,41 |
651,42 |
1915,94 |
0,80 |
0,73 |
|
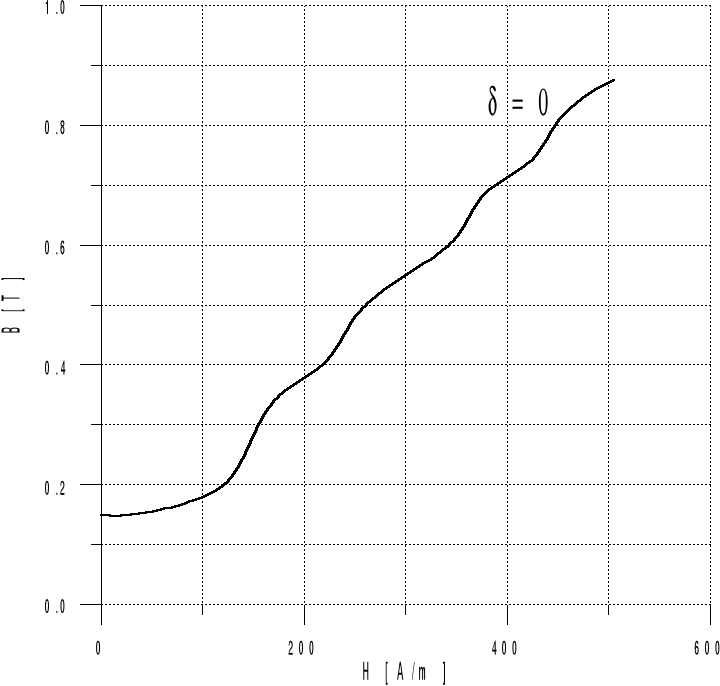
Rys. 2.4. Charakterystyka magnesowania B = f (H) przy d = 0
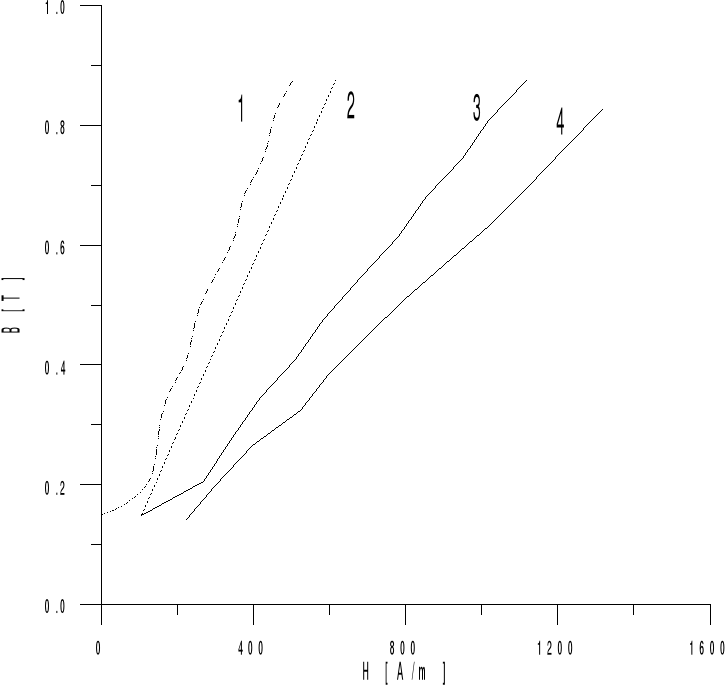
Rys. 2.5. Charakterystyka magnesowania B = f (H) przy d = 0,3
1 - charakterystyka rdzenia
2 - charakterystyka szczeliny
3 - charakterystyka wypadkowa (rdzenia i szczeliny)
4 - charakterystyka wyznaczona na podstawie pomiarów
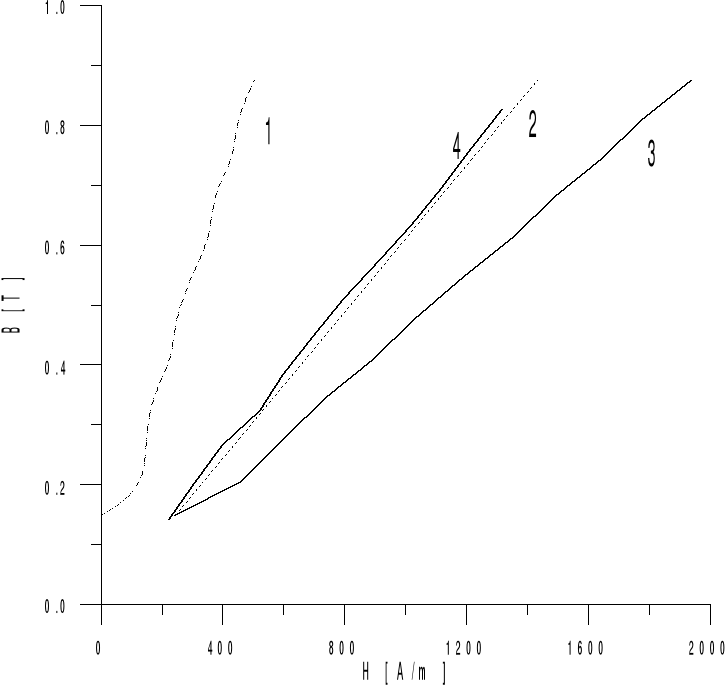
Rys. 2.6. Charakterystyka magnesowania B = f (H) przy d = 0,7
1 - charakterystyka rdzenia
2 - charakterystyka szczeliny
3 - charakterystyka wypadkowa (rdzenia i szczeliny)
4 - charakterystyka wyznaczona na podstawie pomiarów
Badanie rozgałęzionego obwodu magnetycznego.
Rys. 3.1. Układ pomiarowy do badania obwodu magnetycznego.
Tabela 3.2.
z1 |
zp1 |
zp2 |
zp3 |
S1 |
S2 |
S3 |
l1 |
l2 |
l3
|
- |
- |
- |
- |
mm2 |
mm2 |
mm2 |
m |
m |
m |
324 |
586 |
586 |
586 |
1987 |
1987 |
1987 |
0,183 |
0,473 |
0,473 |
Tabela 3.3.
|
Pomiary |
Obliczenia |
||||||||||
Lp |
I1 |
ka |
U1 |
Up1 |
Up2 |
Up3 |
Hm |
F1 |
F2 |
F3 |
Bm |
|
|
A |
- |
V |
V |
V |
V |
A/m. |
mWb |
mWb |
mWb |
T |
|
1 |
0,03 |
1,42 |
20 |
37 |
18 |
14 |
21,04 |
0,28 |
0,14 |
0,11 |
0,14 |
|
2 |
0,05 |
1,42 |
30 |
54 |
23 |
21 |
35,07 |
0,42 |
0,18 |
0,16 |
0,21 |
|
3 |
0,05 |
1,42 |
40 |
70 |
29 |
28 |
35,07 |
0,54 |
0,22 |
0,22 |
0,27 |
|
4 |
0,06 |
1,43 |
50 |
89 |
35 |
34 |
42,38 |
0,68 |
0,27 |
0,26 |
0,34 |
|
5 |
0,07 |
1,43 |
60 |
105 |
42 |
40 |
49,44 |
0,81 |
0,32 |
0,31 |
0,41 |
|
6 |
0,08 |
1,44 |
70 |
122 |
48 |
48 |
56,90 |
0,94 |
0,37 |
0,37 |
0,47 |
|
7 |
0,09 |
1,44 |
80 |
141 |
55 |
54 |
64,01 |
1,08 |
0,42 |
0,42 |
0,55 |
|
8 |
0,11 |
1,45 |
90 |
160 |
64 |
63 |
78,78 |
1,23 |
0,49 |
0,48 |
0,62 |
|
9 |
0,12 |
1,47 |
100 |
175 |
71 |
70 |
87,12 |
1,35 |
0,55 |
0,54 |
0,68 |
|
10 |
0,14 |
1,52 |
110 |
183 |
81 |
80 |
105,10 |
1,41 |
0,62 |
0,61 |
0,71 |
|
11 |
0,18 |
1,65 |
120 |
213 |
90 |
90 |
146,69 |
1,64 |
0,69 |
0,69 |
0,82 |
|
12 |
0,22 |
1,70 |
130 |
230 |
98 |
99 |
184,72 |
1,77 |
0,75 |
0,76 |
0,89 |
|
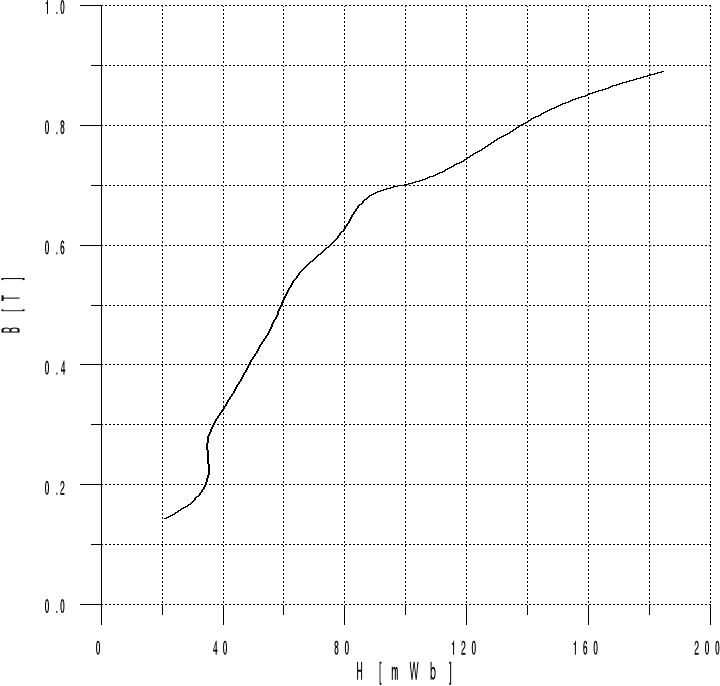
Rys. 3.4. Charakterystyka magnesowania obwodu
Sprawdzenie I prawa Kirchhoffa
Tabela 3.5.
Punkt na |
F1 |
F2 |
F3 |
DF |
DF% |
cha-styce |
mWb |
mWb |
mWb |
mWb |
% |
A |
0,54 |
0,22 |
0,22 |
0,10 |
19 |
B |
1,08 |
0,42 |
0,42 |
0,25 |
23 |
C |
1,77 |
0,75 |
0,76 |
0,25 |
14 |
Sprawdzenie II prawa Kirchhoffa
Tabela 3.6.
Punkt |
F |
B |
H |
Um |
Q
|
DQ% |
|||||
ch-ki |
|
|
z ch-ki magnes. |
napięcia magnet. |
obl. |
Dane |
|
||||
|
F1 |
F2 |
B1 |
B2 |
H1 |
H2 |
H1l1 |
H2l2 |
Um1 + Um2
|
I1kaz1 |
|
|
mWb |
mWb |
T |
T |
A/m. |
A/m. |
A |
A |
A |
A |
% |
A |
0,54 |
0,22 |
0,27 |
0,11 |
35,07 |
18,00 |
6,42 |
8,51 |
14,93 |
23,00 |
35,09 |
B |
1,08 |
0,42 |
0,55 |
0,21 |
64,01 |
35,07 |
11,71 |
16,59 |
28,30 |
41,99 |
32,60 |
C |
1,77 |
0,75 |
0,89 |
0,38 |
184,72 |
45,00 |
33,80 |
21,29 |
55,09 |
121,18 |
54,54 |
Obliczanie parametrów schematu zastępczego i sprawdzenie I prawa Kirchhoffa
Tabela 3.7.
Punkt |
m1 |
m2 |
m3 |
Rm1 |
Rm2 |
Rm3 |
Rmab |
Rm |
ch-ki |
H/m |
H/m |
H/m |
1/H |
1/H |
1/H |
1/H |
1/H |
A |
0,0077 |
0,0056 |
0,0061 |
11960,86 |
42508,45 |
39024,15 |
20345,92 |
32306,79 |
B |
0,0085 |
0,0065 |
0,0078 |
10835,13 |
36622,66 |
30518,89 |
16646,66 |
27481,8 |
C |
0,0112 |
0,009 |
0,0087 |
8223,093 |
26449,7 |
27361,76 |
13449 |
21672,09 |
Tabela 3.7. c.d.
Punkt |
F1 |
Umab |
F2 |
F3 |
DF |
DF% |
ch-ki |
Wb |
A |
Wb |
Wb |
Wb |
% |
A |
0,000501 |
10,20231 |
0,00024 |
0,000261 |
5,42E-20 |
1,08E-14 |
B |
0,000589 |
9,812894 |
0,000268 |
0,000322 |
0 |
0 |
C |
0,000748 |
10,0532 |
0,00038 |
0,000367 |
1,08E-19 |
1,45E-14 |
Wyznaczenie graficzne charakterystyki obwodu
Tabela 3.8.
|
F1 |
Um1 |
F2 |
Um2 |
F3 |
Um3 |
L.p. |
Wb |
A |
Wb |
A |
Wb |
A |
1 |
0,000529 |
0,000156 |
0,000246 |
0,000169 |
0,000246 |
0,000169 |
2 |
0,000623 |
0,00018 |
0,000307 |
0,000206 |
0,000307 |
0,000206 |
3 |
0,000776 |
0,000238 |
0,000369 |
0,000264 |
0,000369 |
0,000264 |
4 |
0,000922 |
0,000293 |
0,000438 |
0,000325 |
0,000438 |
0,000325 |
5 |
0,001061 |
0,000344 |
0,0005 |
0,000378 |
0,0005 |
0,000378 |
6 |
0,001191 |
0,00037 |
0,000569 |
0,000412 |
0,000569 |
0,000412 |
7 |
0,001307 |
0,000389 |
0,00063 |
0,000438 |
0,00063 |
0,000438 |
8 |
0,001445 |
0,000395 |
0,000692 |
0,000441 |
0,000692 |
0,000441 |
9 |
0,001568 |
0,000359 |
0,000769 |
0,00041 |
0,000769 |
0,00041 |
10 |
0,00166 |
0,000339 |
0,000799 |
0,000381 |
0,000799 |
0,000381 |
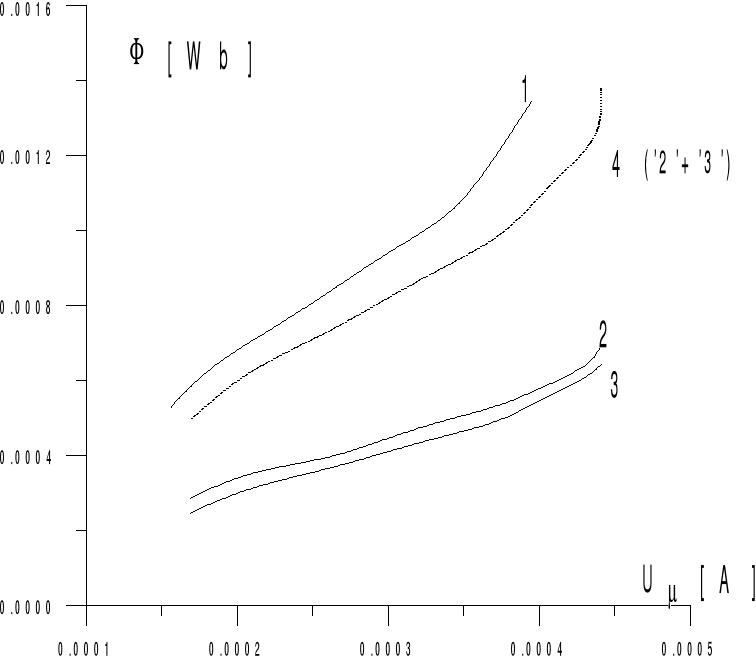
Rys. 3.9. Charakterystyki magnesowania
Wnioski:
Pętla histerezy jest to charakterystyka magnesowania. Na wykresie pętli histerezy magnetycznej możemy ustalić kilka istotnych punktów. Indukcję magnetyczną jaka występuje w rdzeniu przy natężeniu pola magnetycznego równym zeru nazywamy indukcją pozostałości magnetycznej lub indukcją remanencji. Natężenie pola magnetycznego, konieczne do uzyskania indukcji magnetycznej w rdzeniu równej zeru nazywamy natężeniem powściągliwym lub natężeniem koercji. Natężenie (max) pola magnetycznego oraz odpowiadającą mu indukcję magnetyczną nazywamy natężeniem oraz indukcją nasycenia. Dla danej próbki materiału ferromagnetycznego można otrzymać dowolną liczbę pętli histerezy różniących się kształtem , przy czym każda będzie odpowiadała innej wartości maksymalnej natężenia pola magnetycznego. Regulując odpowiednio napięciem zasilającym układ możemy zmieniać kształt krzywej magnesowania na oscyloskopie.
W obwodach magnetycznych źródłem pola magnetycznego może być albo uzwojenie przez które przepływa prąd elektryczny (tak jak w naszym ćwiczeniu) albo magnes trwały, będący ciałem ferromagnetycznym, w którym pole magnetyczne powstało i trwa nadal mimo że w obszarze na zewnątrz ciała prąd elektryczny nie płynie. Zależnie od charakteru prądu płynącego w obwodzie rozróżniamy obwody magnetyczne o strumieniu stałym w czasie i o strumieniu zmiennym w czasie. W naszym ćwiczeniu mieliśmy do czynienia ze strumieniem zmiennym w czasie który wywołany był przez zmienny w czasie prąd elektryczny. Ponadto w przypadku występowania w obwodzie szczeliny powietrznej obwód nasz był niejednorodny ponieważ właściwości magnetyczne powietrza są różne niż właściwości magnetyczne reszty obwodu czyli rdzenia złożonego z transformatorowych blach stalowych. Strumień magnetyczny zamykający się w rdzeniu obwodu magnetycznego nazywamy strumieniem głównym, natomiast strumień zamykający się w środowisku otaczającym ten obwód, nazywamy strumieniem magnetycznym rozproszonym. W obwodach magnetycznych wykonanych z materiałów ferromagnetycznych strumień rozproszenia można pominąć.
W naszym ćwiczeniu do badania rozgałęzionego obwodu magnetycznego używaliśmy transformatora trójfazowego o rdzeniu zbudowanym z wzajemnie izolowanych blach transformatorowych. Izolowanie blach jest konieczne ze względu na konieczność ograniczenia prądów wirowych, które mogą powodować nagrzewanie się rdzenia.
Zasada działania wielu urządzeń elektrycznych opiera się na przepływie strumienia magnetycznego w ferromagnetyku np: transformatory, dławiki, wzmacniacze magnetyczne(wzmacniacze dużych mocy), elektromagnesy itp.
Wyszukiwarka
Podobne podstrony:
05', Politechnika Lubelska
05', Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, sprawozdania, Sprawozdania, Labo
05, Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, sprawozdania, Sprawozdania, Labor
05'' 3, POLITECHNIKA LUBELSKA
05''''', POLITECHNIKA LUBELSKA
05''''' 2, POLITECHNIKA LUBELSKA
05 7, POLITECHNIKA LUBELSKA w LUBLINIE
Laboratorium elektroniki - Ćwiczenie 05, Politechnika Lubelska, Studia, sem III, materiały, Teoria O
11 Silnik indukcyjny pierścieniowy SUHf, Szkoła, Politechnika 1- 5 sem, SEM IV, Maszyny Elektryczne.
05 h zaokrąglanie, Politechnika Lubelska, Studia, Studia, organizacja produkcji, laborki-moje, Wydzi
ćw.5, 05 Gorski, Politechnika Krakowska
Wyznaczanie charakterystyki fotokomórki gazowanej 05, Uczelnia - Politechnika Slaska, Fizyka
05. Karta technologicza zbiorcza, Politechnika Lubelska, Studia, Studia, Sprawka 5 semestr, technolo
Politechnika Białostocka 05 Realizacja pneumatycznych układów sterowania sekwencyjnego
więcej podobnych podstron