Na podstawie rozkładu prawdopodobieństwa zmiennej losowej X
xi |
1 |
3 |
6 |
8 |
pi |
0,2 |
0,1 |
0,3 |
0,4 |
Wyznaczyć
wykres rozkładu prawdopodobieństwa
dystrybuantę
wykres dystrybuanty
Badano ile studenci II roku C geologii poświęcają czasu na przygotowanie się do zajęć ze statystyki. Otrzymano następujące wyniki w min:
10, 20, 15, 0, 15, 30, 30, 20, 10, 15, 10, 60, 0, 10, 30, 20, 120, 60, 10, 120,
proszę przedstawić wyniki na wykresie funkcji prawdopodobieństwa, wyznaczyć dystrybuantę i przedstawić ją w postaci graficznej. Policzyć funkcje przewyższenia R(x)=P(X≥x)
Dana jest dystrybuanta zmiennej losowej X:
xi |
(-∞, -2] |
(-2,0] |
(0,3] |
(3,4] |
(4,+ ∞) |
F(xi) |
0 |
0,2 |
0,4 |
0,8 |
1 |
Wyznacz
wykres dystrybuanty
funkcje prawdopodobieństwa i jej wykres
Obliczyć prawdopodobieństwo P(0≤x<3)
Dana jest dystrybuanta zmiennej losowej X
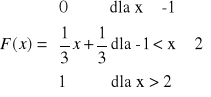
Obliczyć, z jakim prawdopodobieństwem zmienna losowa X w wyniku doświadczenia przyjmie wartość należącą do przedziału (0; 1).
Dana jest dystrybuanta zmiennej losowej X
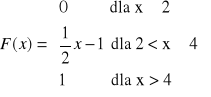
Obliczyć, z jakim prawdopodobieństwem zmienna X w wyniku doświadczenia przyjmie wartość należącą do przedziału (2; 3).
Dana jest funkcja gęstości prawdopodobieństwa zmiennej losowej X
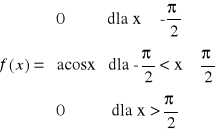
Znaleźć stałą a oraz dystrybuantę.
Pomiar natężenia pola magnetycznego nad pewną kopalnią można przedstawić w przybliżeniu za pomocą funkcji gęstości prawdopodobieństwa:
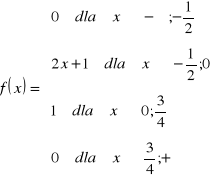
Wyznaczyć dystrybuantę F(x),
!!! w każdym zadaniu f. gęstości i dystrybuanty
proszę przedstawić w postaci graficznej!!!
Zmienna losowa dyskretna. Charakterystyki funkcyjne i liczbowe.
Wyznaczyć wartość przeciętną (oczekiwaną) i wariancje zmiennej losowej:
U1=2X+1
U2=X2
U3=-X2+2
Jeżeli EX=2 D2X=1 EX4=34
Dane są rozkłady niezależnych zmiennych losowych dyskretnych:
X= 1 2 Y= 0.5 1
P(X)= 0.2 0.8 P(Y)= 0.3 0.7
Obliczyć wartość oczekiwaną iloczynu XY
Dane są rozkłady niezależnych zmiennych losowych dyskretnych:
X= 1 2 Y= 0.5 1
P(X)= 0.2 0.8 P(Y)= 0.3 0.7
Obliczyć wartość oczekiwaną sumy X+ Y.
Obliczyć drugi moment początkowy, wariancję (dwoma sposobami) odchylenie standardowe, , modę i medianę zmiennej losowej X, mając jej rozkład
X= 0.1 2 10 20
P(X)= 0.4 0.2 0.15 0.25
Zmienna losowa X może przyjąć tylko dwie możliwe wartości: x1 z prawdopodobieństwem 0.3 i x2 z prawdopodobieństwem 0.7, przy czym x2 > x1. Obliczyć x1 i x2 wiedząc, że E[X] = 2.7, var(X) = 0.21.
Dla zmiennej losowej X która ma funkcję prawdopodobieństwa postaci
W wyższej szkole prywatnej uczy się 1000 studentów. Badamy zmienną losową X zdefiniowaną jako liczba podręczników przyniesionych na zajęcia przez losowo wybranego studenta w dniu 29 marca 2000 roku (przyjmujemy, że wszyscy studenci byli tego dnia w szkole). Załóżmy, że rozkład liczby podręczników wśród studentów wyglądał następująco
Dystrybuanta F zmiennej losowej X jest określona następującą tabelką:
Wykonując pewien eksperyment uzyskano następujące wyniki:
3, 1, 2, 2, 6, 1, 2, 3, 3, 6, 5, 6, 6, 6, 1, 1, 2, 3, 5, 6.
Proszę przedstawić wyniki na wykresie funkcji prawdopodobieństwa, wyznaczyć dystrybuantę, wartość oczekiwaną medianę kwantyl x0.75. Obliczyć prawdopodobieństwo P(2< x ≤ 5),
P(2< x <5), P(2≤ x ≤ 5), P(2≤ x < 5), P(x> 2), P(x ≥ 2), P(x < 5), P(x Ⴃ 5).Zmienna losowa X ma rozkład:
Niech dystrybuanta f ciągłej zmiennej losowej X wynosi
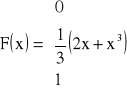
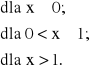
a). Znajdź f gęstości zmiennej losowej X oraz prawdopodobieństwo P(X>0.5)
b). Obliczyć wartość oczekiwaną, wariancje.Czas reakcji X na pewien typ bodźca jest ciągłą zmienną losową o dystrybuancie:
Zmienna losowa X ma rozkład o dystrybuancie:
Dla rozkładu o dystrybuancie
Dystrybuanta zmiennej losowej X jest dana wzorem (rozkład potęgowy):
Dana jest dystrybuanta rozkładu zmiennej T:
Pomiar natężenia pola magnetycznego nad pewną kopalnią można przedstawić w przybliżeniu za pomocą funkcji gęstości prawdopodobieństwa:
Dobrać tak stałą c
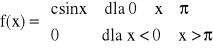
była gęstością, a następnie: Obliczyć medianę, kwantyl rzędu ¼ oraz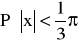
.Zmienna losowa X ma rozkład gęstości :
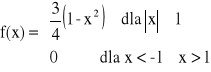
Naszkicować wykres gęstości. Wyznaczyć wartość przeciętną, modę, medianę.Zmienna losowa X ma rozkład o gęstości
xi |
-3 |
-1 |
3 |
5 |
pi |
0.1 |
0.2 |
0.5 |
0.2 |
Wyznaczyć;
wartość oczekiwaną,medianę,kwantyl x0,3, wariancję (dwoma sposobami), odchylenie standardowe, drugi moment początkowy, trzeci moment początkowy, trzeci moment centralny, współczynnik asymetrii CS, współczynnik zmienności CV, kurtozę (współczynnik skupienia) Ce
Liczba podręczników |
0 |
1 |
2 |
3 |
4 |
5 |
Liczba studentów |
100 |
300 |
250 |
200 |
100 |
50 |
a). obliczyć funkcje prawdopodobieństwa, dystrybuantę
b). Obliczyć wartość oczekiwaną, wariancję, modę, medianę, kwantyl rzędu x0.75
x |
(-∞,1] |
(1,3] |
(3,6] |
(6,∞) |
F(x) |
0 |
0,3 |
0,6 |
1 |
Wyznaczyć funkcje prawdopodobieństwa tej zmiennej, wartość oczekiwaną, wariancje, medianę, kwantyl x0,3, odchylenie standardowe, modę.
xi |
-1 |
0 |
2 |
3 |
pi |
0.1 |
0.4 |
0.2 |
0.3 |
Wyznaczyć wartość oczekiwaną i wariancję zmiennej losowej U = 3X + 4, korzystając z odpowiednich własności wartości oczekiwanej i wariancji.
Zmienna losowa ciągła. Charakterystyki funkcyjne i liczbowe.
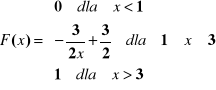
Obliczyć prawdopodobieństwo, że X znajdzie się w przedziale [1.5; 2.5] a następnie wartość oczekiwaną zmiennej losowej X.
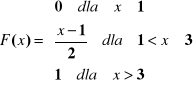
Wyznaczyć wartość oczekiwaną drugi moment początkowy, medianę, kwantyl rzędu 0.4 funkcję przewyższenia oraz odchylenie standardowe zmiennej losowej X.
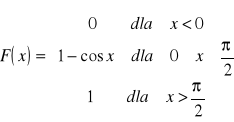
wyznacz funkcję przewyższenia wartość oczekiwaną modę i medianę.
Wyznaczyć funkcję gęstości prawdopodobieństwa oraz wariancję zmiennej X jeśli: b=2 , xm=9.
; (λ>0)
Wyznaczyć funkcję gęstości prawdopodobieństwa i wartość oczekiwaną zmiennej T.
Uwaga: (a>0)
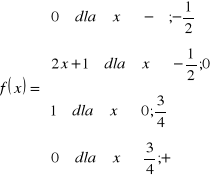
Wyznaczyć dystrybuantę F(x), oraz policzyć ![]()
![]()
gdzie c jest stałą dodatnią. Wyznaczyć wartość stałej c a następnie wartość oczekiwaną i odchylenie standardowe zmiennej losowej X.
!!! w każdym zadaniu f. gęstości i dystrybuanty
proszę przedstawić w postaci graficznej!!!
Wyszukiwarka
Podobne podstrony:
Tabelka Geometria Wykreślna, Pliki, Studia PK (Mechaniczny & WIL), Geometria wykreślna
Lab16 (1), Pliki, Studia PK (Mechaniczny & WIL), Fizyka, Laboratoria, Lab 16
eko odp mini, Pliki, Studia PK (Mechaniczny & WIL), Ekologia
Zadanie nr 3, Studia PK, Budownictwo Ogólne
3 zmienna losowa i rozkład normalny
Zadanie nr 1, Studia PK, Budownictwo Ogólne
Zadanie nr 2, Studia PK, Budownictwo Ogólne
Maliszewski Jacek Ekonometryczna analiza zmienności oraz rozkłady prawdopodobieństwa rtf
Zadania z, Studia, PK OŚ, technologia informacyjna, exel
36 ?finicja zmiennej losowej Zmienna losowa i jej rozkład
geometria analityczna zadania, Studia PK WIS, Sem 3 IS, Geometria analityczna
2 zmienna losowa zadania
zmienna losowa i jej rozklad
11 Zadania kontrolne geometria analityczna(2), Studia PK WIS, Sem 3 IS, Geometria analityczna
ZAD2-Naryswoać układ Arona do pomiaru mocy czynnej, Studia PK, Semestr III, Metrologia, Zadania Goto
więcej podobnych podstron