BŁĘDY POMIARU - NIEPEWNOŚC WYNIKU POMIARU

ŹRÓDŁA BŁĘDÓW

- niedoskonałość narzędzi pomiarowych BŁĄD PRZYRZĄDU

- uproszczenia metod pomiarowych BŁĄD METODY

- zakłócenie od wpływów obcych (temperatura) BŁĄD WPŁYWU

- predyspozycje fizyczno-psychiczne człowieka BŁĄD PERSONALNY

CHARAKTER BŁĘDÓW

• systematyczne; przyczyny znane, wartość stała lub zmienna wg stałego prawa

• przypadkowe; bez względu na źródło model błędu ma charakter stochastyczny, losowy

• grube, pomyłki; awaria, nieuwaga

DEFINICJE

• błąd bezwzględny Δ = X_m - X_r

• błąd względny δ = Δ / X_r

• błąd względny zakresowy δ_z = Δ / Z

• błąd maksymalny; największa wartość błędu z serii pomiarów tej samej wielkości lub pomiarów wykonywanych na całym zakresie narzędzia

• błąd graniczny Δ_g , takie że X_r = X_m ± Δ_max

• błąd graniczny względny

• klasa przyrządu (analogowego)
  

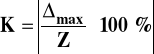
• błąd przyrządu cyfrowego δ_c ⁼ δ [%] ± δ_z [%]

NIEPEWNOŚĆ POMIARU

Dokładność pomiaru - stopień godności wyniku pomiaru z wartością rzeczywistą wielkości mierzonej.

Niedokładność pomiaru - im dokładniejszy pomiar tym mniejsza niedokładność

Przedziałowa interpretacja niedokładności wyniku pomiaru traktuje wynik nie jako punkt na osi liczbowej x_m lecz jako przedział wokół X(x_m) zwany przedziałem niepewności wyniku pomiaru, w którym leży nieznana wartość prawdziwa x_r.

Ponieważ każdy kolejny wyznaczony przedział niepewności jest przedziałem niepewności, za miarę niedokładności pomiaru uznaje się najmniejszy możliwy do wyznaczenia przedział niepewności wyniku pomiaru.

Przedział niepewności wyniku pomiaru określa się najczęściej jako przedział symetryczny podając estymatę x_m i graniczny błąd pomiaru Δ_gmax .

Rozróżnia się dwa typy modeli niedokładności pomiaru:

• model deterministyczny

• model losowy

MODEL DETERMINISTYCZNY NIEDOKŁADNOŚCI POMIARU

Zakłada się, że prawdziwa wartość x_m jest nieznana, ale leży wewnątrz przedziału niepewności i hipotetyczne powtarzanie pomiaru w warunkach powtarzalności daje zawsze takie same wyniki estymaty x_m i błędu granicznego Δ_gmax.

Błąd graniczny wyznaczany jest na podstawie danych technicznych narzędzi stosowanych w pomiarze a zawartych w ich instrukcjach lub świadectwach legalizacyjnych.

PRZYKŁADY WYZNACZANIA BŁĘDÓW GRANICZNYCH W PRZYPADKACH POMIARÓW BEZPOSREDNICH I POŚREDNICH

1. Wyznaczanie klasy przyrządu analogowego i błędu w pomiarze bezpośrednim

Woltomierz elektromagnetyczny o zakresie 120 V sprawdzono woltomierzem elektromagnetycznym wzorcowym klasy 0.2 i zakresie 150 V. Pomiarów dokonano dla każdej ocyfrowanej działki badanego woltomierza i wyniki przedstawiono w tabelce. Należy wykonać wykres poprawek i obliczyć klasę sprawdzanego woltomierza.

Ub [V]	0	10	20	30	40	50	60	70	80	90	100	110	120
Uw [V]	0,0	9,5	21,0	30,5	41,0	50,0	59,5	69,5	79,0	88,0	98,2	109,3	119,5

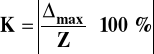
Δ

0.0

0.5

-1.0

-0.5

-1.0

0.0

0.5

0.5

1.0

2.0

1.8

0.7

0.5

Δ_max = 2.0 [V]

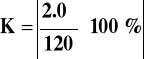
= 1.6666(6)

Klasa - 0.01, 0.02, 0.05, 0.1, 0.2, 0.5, 1, 2, 5

Klasa badanego woltomierza wynosi 2.

Woltomierzem tym zmierzono napięcie na stronie wtórnej pewnego transformatora. Uzyskano wynik U_m = 110 [V].

Δ_max tego woltomierza - klasa 2, zakres 120 [V] wynosi - Δ_max = K . Z / 100

Δ_max = 2 .120 /100 = 2.4 [V]

Wartość rzeczywista mierzonego napięcia mieści się w przedziale:

U_r = U_m ± Δ_max U_r = 110 ± 2.4 [V]

2. Wyznaczanie błędu przyrządu cyfrowego i błędu bezpośredniego pomiaru tym przyrządem

Dokładność wskazań cyfrowego woltomierza o parametrach - zakres 4 [V], błąd ±(0.1 % wielkości mierzonej + 0.025 % wielkości zakresowej), sprawdzano poprzez porównanie ze wskazaniami cyfrowego woltomierza uznanego za wzorcowy o parametrach - błąd ±(0.05 % rdg + 3 dgt) i zakres 5 [V]. Za pomocą precyzyjnego dzielnika napięcia na woltomierzu badanym nastawiano żądaną wartość napięcia a wartość rzeczywistą tego napięcia odczytywano na woltomierzu wzorcowym. Wyniki porównania w dziewięciu punktach zamieszczono w tabelce. Czy wskazania badanego przyrządu mieszczą się zadeklarowanej wartości jego błędu? Zapisz błąd woltomierza wzorcowego w taki sam sposób jak jest zapisany dla woltomierza badanego.

Ub [V]	0.000	0.500	1.000	1.500	2.000	2.500	3.000	3.500	3.999
Uw [V]	0.005	0.495	1.007	1.497	2.012	2.529	2.966	3.464	3.969

Δ [V]	-0.005	-0.005	-0.007	+0.003	-0.012	-0.029	+0.034	+0.036	+0.030
δ [%]		-1.0	-0.7	+0.2	-0.6	-1.16	+1.13	+1.03	+0.75
Δz [%]	-0.125	-0.125	-0.175	+0.075	-0.300	-0.725	+0.850	+0.900	+0.750

Błąd = ±(1.16 % w. mierzonej + 0.9 % w. zakresowej)

Błąd woltomierza wzorcowego:

błąd ±(0.05 % rdg + 3 dgt)

3 dgt = 0.003 (3 z najniższej pozycji odczytu) 0.003/5 = 0.06 %

błąd ±(0.05 % w. mierzonej + 0.06 % w. zakresowej)

Woltomierzem tym zmierzono napięcie wyjściowe pewnego wzmacniacza.

Wynik pomiaru U_m = 3.665 [V].

Wartość rzeczywista napięcia mieści się w przedziale (obliczenie wg instrukcji):

U_r = 3.665 ±(0.1 % w. mierzonej + 0.025 % w. zakresowej)

U_r = 3.665 ±(0.003665 + 0.001) = 3.665 ±(0.004 + 0.001) = 3.665 ± 0.005 [V]

3. Wyznaczanie błędów przy pomiarze pośrednim

W pomiarze pośrednim wielkość mierzona Y jest wyznaczana jako funkcja innych wielkości - X_j (gdzie j= 1,2,3,...k) mierzonych bezpośrednio.

Błędy pomiarów poszczególnych wielkości X_j decydują o błędzie z jakim jest wyznaczana wartość wielkości Y. Mówimy o prawie przenoszenia (propagacji) błędów.

Jeżeli Y = F (X₁ , X₂ , X₃ , X₄ , ..., X_k)

To błąd względny graniczny określenia wielkości Y wyznaczamy na ogół metodą różniczki zupełnej:

δ_Y = Δ_Y/Y =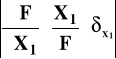
+
+... +

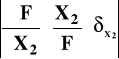
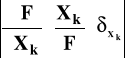
δ_Xj - wylicza się z danych technicznych (klas, błędów) używanych przyrządów.

WZORY UPROSZCZONE

Y=X₁ ± X₂ ΔY = |ΔX₁| + |ΔX₂|

Y= X₁ . X₂ ΔY = | X₂ ΔX₁| + | X₁ΔX₂|

Y= X₁ / X₂ ΔY = |ΔX₁/ X₂ | + | X₁/ X₂ ² .ΔX₂|

Y=Xⁿ ΔY= | n.X^n-1 ΔX₁|

Przykład

Dla określenia wartości mocy prądu stałego wydzielonej na pewnym odbiorniku zmierzono prąd i napięcie na tym odbiorniku. Używano woltomierz o danych: zakres 10 V, klasa 0.5, i amperomierz o danych: zakres 5 A i klasa 1.

Uzyskano następujące wyniki: U = 6.25 V, I = 2.17 A.

P=U.I P = 6.25. 2.17 = 13.5625 W

ΔP = |I.Δ U| + |U.Δ I|

Δ U =K.Z/100 = 0.5.10/100 = 0.05 V

Δ I = K.Z/100 = 1.5/100 = 0.05 A

ΔP = 2.17 . 0.05 + 6.25 . 0.05 = 0.421 W

P_r = 13.5625 ± 0.421 W

MIEJSCA ZNACZĄCE I DOKŁADNOŚĆ ZAPISYWANIA WYNIKU POMIARU

Miejsca znaczące zapisu wyniku pomiaru to miejsca pewne.

Cyfra na ostatnim miejscu znaczącym jest pewna wtedy gdy błąd pomiaru jest mniejszy niż połowa jednostki tego miejsca znaczącego.

1974.500 7 miejsc znaczących

1. 2 miejsca znaczące

Błędy graniczne zapisuje się z jedną (najwyżej wyjątkowo) z dwoma liczbami znaczącymi :

Z obliczeń Zapisujemy

W= 2.494, ΔW = ±0.043 W = 2.49 ± 0.05

W= 237.465, ΔW = ±0.127 W = 237.5 ± 0.2

W= 123375, ΔW = ±678 W = 123400 ± 700

W przypadku ostatniego zadania:

P_r = 13.5625 ± 0.421 W P_r = 13.6 ± 0.5 W

MODEL LOSOWY NIEDOKŁADNOŚCI POMIARU

Zakłada się, że hipotetyczne powtarzanie pomiaru w warunkach powtarzalności, prowadzi do randomizacji estymaty x_m (staje się ona zmienną losową) co pociąga na ogół także, randomizację błędu granicznego Δ_gmax. Przedział niepewności staje się przedziałem losowym (jego granice są zmiennymi losowymi). Mówimy więc, że rzeczywista wartość wielkości mierzonej znajduje się wewnątrz pewnego przedziału z prawdopodobieństwem - p, gdzie p - jest poziomem ufności. Niepewność pomiaru wyraża się za pomocą niepewności standardowej i niepewności rozszerzonej.

Niepewność standardowa u(x_m) jest odchyleniem standardowym lub estymatą odchylenia standardowego randomizowanej estymaty X_m . Przedział niepewności wyrażony za pomocą niepewności rozszerzonej U(x) ma postać:

[ X_m - U(x_m), X_m + U(x_m) ]

Niepewność rozszerzona i standardowa związane są zależnością:

U(x_m) = k_p . u(x_m)

Gdzie k_p jest współczynnikiem rozszerzenia o wartości zależnej od przyjętego poziomu ufności p i kształtu rozkładu prawdopodobieństwa randomizowanej estymaty X_m. Typowe wartości współczynnika rozszerzenia to 2 i 3 i przypisuje się im odpowiednio poziomu ufności p=0.95 i p=0.99.

Rozróznia się dwie metody obliczania niepewnośći:

Metoda typu A - Obliczanie na podstawie analizy statystycznej serii wyników pojedynczych pomiarów w tych samych warunkach. Jeśli poszczególne (j-te) wyniki w serii wynoszą x₁, x₂, x₃,..., x_n ,to

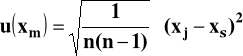
gdzie :x_s - wartość średnia arytmetyczna wyników.

Metoda typu B - Obliczanie niepewności metodami innymi niż analiza statystyczna, przeważnie na podstawie danych o stosowanych przyrządach pomiarowych (np. klasy czy błędy graniczne)

Niepewności typu A i B składają się na niepewność estymaty X_m przy czym sumowaniu podlegają kwadraty niepewności zgodnie z zależnością:

U² (x_m) = U² _A (x_m) + U² _B (x_m)

W pomiarach pośrednich na podstawie równania pomiaru tworzy się prawo propagacji błędów będące probabilistycznym odpowiednikiem klasycznego prawa :

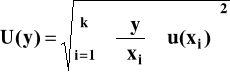
7

---