Zakład Chemii Fizycznej

Laboratorium Studenckie

SPRAWOZDANIE

ĆWICZENIE 26

ZALEŻNOŚĆ SEM OGNIWA OD TEMPERATURY

WYKONALI:

Kozieł Urszula

Piotr Gawroński

Technologia Chemiczna

rok III grupa II

SZCZECIN 2002r

CEL ĆWICZENIA:

Celem ćwiczenia jest wyznaczenie zależności SEM ogniwa od temperatury.

WSTĘP:

W przeprowadzonym ćwiczeniu użyto nasyconej elektrody kalomelowej oraz platynowej zanurzonej w r-rze 0,1m J₂ w 4% KJ. Po ustaleniu się stanu równowagi tegoż układu, zmnieniając kolejno temperaturę termostatu i regulując przepływ wody chłodzącej, dokonano pomiarów siły elektromotorycznej ogniwa SEM.

W ogniwie zaszły następujące procesy:na anodzie: reakcja utleniania

2Hg = 2Hg⁺ +2e

2Hg+ + 2Cl^- = Hg₂Cl_2(s)

2Hg + Cl^- = Hg₂Cl_{2 (s)} + 2e

na katodzie: reakcja redukcji

J₂ + 2e = 2J^-

Pomiaru SEM przez miliwoltomierz V-544 -różnicy potencjałów elektrod zmierzoną dla ogniwa przez które nie płynie prąd elektryczny, dokonywano dla temperatur 25, 30, 35, 40, i 450C co 3 minuty. Po ustaleniu się wskazań miliwoltomierza, przyjęto wynik jako prawidłowy.

Na podstawie odczytanych wartości siły elektromotorycznej układu, możliwe stało się określenie efektu cieplnego ΔH reakcji oraz zmianę entalpii swobodnej ΔG a także entropię ΔS.

W tym celu posłużono się równaniem Gibbsa i Helmholtza:

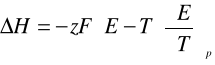
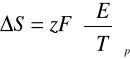
Zależność entalpii i entropii reakcji zachodzącej w ogniwie wiąże się także ze wzorem, który ujmuje zależność pomiędzy entalpią swobodna a siłą elektromotoryczną (E), czyli

gdzie: ΔG - entalpia swobodna

ΔH - entalpia

ΔS - entropia

z - liczba moli elektronów wymieniona w reakcji (tu: z = 2)

E - zbadana siła elektromotoryczna

F- stała Faradaya =96485,3 [C/mol]

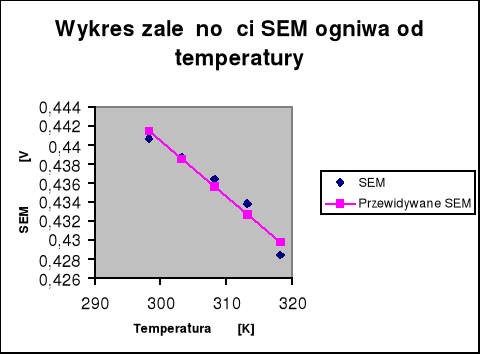
Zestawienie wyników:

T [^0C]	T [K]	SEM [V]
25	298,15	0,4406
30	303,15	0,4386
35	308,15	0,4364
40	313,15	0,4338
45	318,15	0,4285

Opracowanie wyników:

1. Sumaryczne równanie reakcji odpowiedzialnej za pracę ogniwa:

J₂ + 2Hg +2Cl^- = Hg₂Cl_2(S)+ 2J^-

2. Schemat używanego ogniwa zgodny z konwencją sztokholmską:

Hg I Hg₂Cl_2(s) I Hg₂Cl_2(nas.),KCl_(nas.) I KJ_(4%) II KJ_(4%)I J_{2 (0,1m)} I J₂ I Pt

3. Równanie Nernsta na SEM badanego ogniwa:

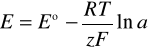
4. Odnalezione w literaturze potencjały normalne elektrod używanych w doświadczeniu:

- elektroda kalomelowa : + 0,2420 V,

- elektroda platynowa : + 0,536 V.

5. Z różnicy potencjałów obliczamy normalną siłę elektromotoryczną ogniwa

= + 0,536 - 0,242041 = 0,294 [V]

6. Z równania Nernsta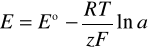

uwzględniając aktywności produktów i substratów (przyjmując dla ciał stałych a=1) otrzymujemy wzór:

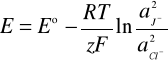
Dla SEM zmierzonej w warunkach standardowych

E= 0,4406 [V]

E⁰ = 0,294 [V]

R = 8,314 [J/K*mol]

z = 2

F = 96485,3 [C/mol]

otrzymujemy wzór na stosunek aktywności jonów J^-/Cl^-

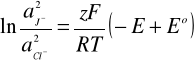
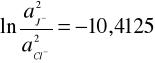
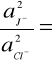
e^-10,4125 = 3*10^-5

7. Wykres zależności E = f(T):

8. Wyznaczenie wartości współczynnika temperaturowego:

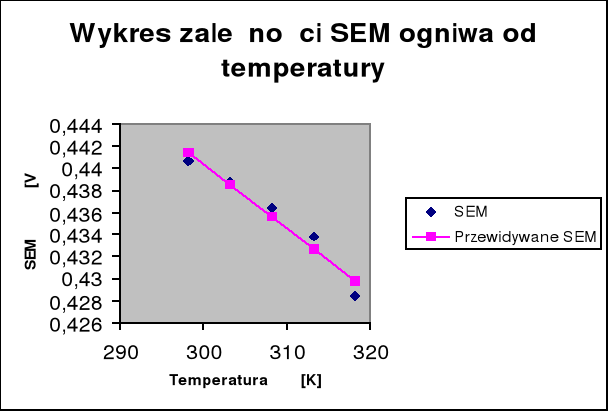
Współczynnik kierunkowy (a) prostej o równaniu ogólny y=ax+b

wynosi -0,00058 , czyli:

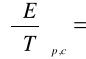
-0,00058 [V/K]

9. Ze wzoru Gibbsa-Helmholtza wyznaczamy wartości entalpii ΔH, entalpii swobodnej ΔG oraz entropii ΔS z jakimi przebiegała reakcja:

Dla T=298,15 [K]

E=0,4406 [V]

F=96485,3 [C/mol]

(dE/dT)_p= -0,00058 [V/K]

z=2

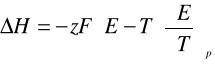
ΔH= -2 * 96485,3 *[ 0,4406 - 298,15 * (-0,00058)]= -118392,6733 [J/mol]

ΔH= -118,38926733 [kJ/mol]

Dla T=298,15 [K]

E=0,4406 [V]

F=96485,3 [C/mol]

(dE/dT)_p= -0,00058 [V/K]

z=2

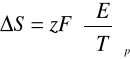
ΔS = 2 * 96485,3 * (-0,00058)

ΔS = -111,9229 [J/mol*K]

Dla E=0,4406 [V]

F=96485,3 [C/mol]

z=2

ΔG = -2 * 96485,3 * 0,4406 = 85022,84636 [J/mol]

ΔG = -85,02284636 [kJ/mol]

---