KUJAWA EWELINA

KATARZYNA KAMASZKO

ĆWICZENIE NR 7

TEMAT: ADSORPCJA NA GRANICY FAZ ROZTWÓR - GAZ. IZOTERMA ADSORPCJI GIBBSA.

Właściwością odróżniającą ciecz od gazu jest napięcie powierzchniowe. Napięcie międzyfazowe warunkuje spójność cieczy i powstanie powierzchni międzyfazowej ciecz-gaz.

Cząsteczka znajdująca się wewnątrz fazy ciekłej jest mniej więcej równomiernie otoczona przez inne cząsteczki, a siły z jakimi one na nią oddziaływują praktycznie kompensują się, więc ich wypadkowa równa jest zeru. Cząsteczki, które leżą na graniczącej z fazą gazową powierzchni cieczy ulegają oddziaływaniu cząsteczek z wnętrza cieczy. Dzieje się tak, ponieważ oddziaływanie cząsteczek powierzchniowych z cząsteczkami gazu nad powierzchnią są znikomo małe w porównaniu z siłami oddziaływania z cząsteczkami cieczy. Powoduje to, że każda cząsteczka cieczy znajdująca się w warstwie powierzchniowej doznaje jednostronnego przyciągania od strony cząsteczek cieczy, a wypadkowa sił działa prostopadle do powierzchni i jest skierowana do wnętrza cieczy, a więc cząsteczka cieczy w warstwie powierzchniowej znajduje się pod działaniem sił wciągających ją do wnętrza cieczy. Wskutek tego działania, obok ciśnienia wewnętrznego występuje zjawisko napięcia powierzchniowego.

Napięcie powierzchniowe σ jest to zmniejszenie potencjału termodynamicznego układu G towarzyszące zmniejszeniu się jego powierzchni A o jednostkę

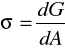
lub siła styczna do powierzchni potrzebna do rozerwania błonki powierzchniowej na długości jednostkowej. Wymiar tej wielkości jest J/m² lub N/m.

Istnieje szereg metod pomiaru napięcia powierzchniowego, które można podzielić na statyczne i dynamiczne. Najbardziej dogodne do oznaczania napięcia powierzchniowego cieczy i roztworów są następujące metody:

• kapilarnego wzniesienia,

• kroplowa,

• pęcherzykowa,

• Wilhelmy'ego,

• profilu leżącej kropli.

Szczegółowe rozważania dotyczące adsorpcji na granicy faz roztwór-gaz przeprowadził Gibbs. Równanie Gibbsa zwane izotermą adsorpcji ustala zależność między nadmiarem powierzchniowym zaadsorbowanych cząsteczek (jonów) i- tej substancji (Г_i), jej potencjałem chemicznym (μ_i) oraz napięciem powierzchniowym (σ). Równanie izotermy Gibbsa w stałej temperaturze i przy stałym ciśnieniu ma postać:

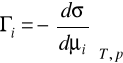
Metoda pęcherzykowa polega na powolnym wdmuchiwaniu pęcherzyków powietrza do badanej cieczy za pomocą kapilary, której wylot znajduje się pod powierzchnią cieczy. Względne pomiary napięcia prowadzi się używając jako cieczy wzorcowej wody. W metodzie tej posługuje się zależnością:

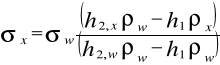
Stęż.C2H5OH (% wag.)	0	10	20	30	40	50	60	70	80
Ciśn. manom. pm (mmHg)	68	62	54	46	43	41	40	38	35
Napięcie pow. (N/m)	0,05067	0,04391	0,03566	0,02704	0,02416	0,02245	0,02192	0,02139	0,01754

Obliczanie napięcia powierzchniowego:

ρ_w-gęstość wody (kg/m3)

ρ_x -gęstość badanej cieczy (kg/m3)

h_2x -różnica poziomów wody w ramionach manometru, gdy badamy roztwór alkoholu (m)

h_2w - różnica poziomów wody w ramionach manometru, gdy badana cieczą jest woda (m)

h₁ - głębokość zanurzenia kapilary (m)

σ_w - napięcie powierzchniowe wody (N/m)

σ_x - napięcie powierzchniowe badanej cieczy (N/m)

Pomiar został wykonany w temp. 22˚C i dla tych warunków przyjmujemy:

σ_w = 0,07244 N/m

ρ_w = 998 kg/m³

h₁ = 23*10^-3 m

h_2,w = 87,33 * 10^-3 m

np.

0,05067

Obliczanie aktywności alkoholu etylowego:

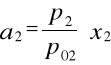
gdzie:

p₂ - prężność alkoholu nad jego roztworem wodnym

p₀₂ - prężność alkoholu nad czystym etanolem

Lp.	Stęż. C2H5OH (% wag.)	X1	X2	ρ (g/cm3)	p2 (mmHg)	a2	σ (N/m)		z (10^-3)	Γ2(10^-6) (mol/m^2)
1	0	1,00	0	0,998	0	0	0,07244		0	0
2	10	0,458	0,042	0,9982	6,7	0,00645	0,04729	-9,33	28	2,04
3	20	0,911	0,089	0,969	12,6	0,02572	0,04092	-2,4	24	1,76
4	30	0,857	0,143	0,954	17,1	0,05608	0,03793	-1,05	23	1,63
5	40	0,794	0,206	0,935	20,7	0,0978	0,03128	-0,56	22	1,53
6	50	0,719	0,281	0,914	23,5	0,15146	0,03109	-0,34	21	1,48
7	60	0,631	0,369	0,891	25,6	0,21666	0,03017	-0,23	20	1,42
8	70	0,524	0,476	0,868	28,0	0,30569	0,02815	-0,16	19	1,38
9	80	0,391	0,609	0,843	31,2	0,4358	0,02767	-0,08	13	1,33

Przykład obliczania nadmiarów powierzchniowych metodą analityczną:

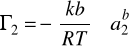
k=0,03

b= -0,1

R=8,31438 J/mol*K

T=295,15 K

a₂=0,02572

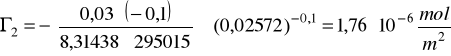
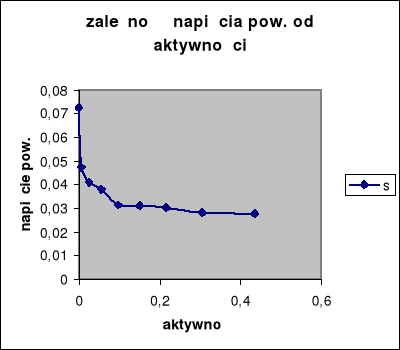
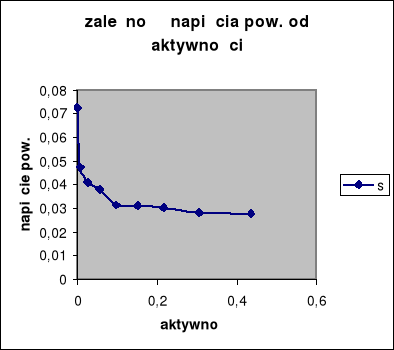
Przykład obliczania nadmiarów powierzchniowych metodą graficzną:

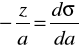
a₂=0,00645

z=0,028 (w jednostkach napięcia powierzchniowego J/m²)

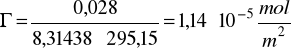
Porównanie wyników uzyskanych metodą graficzną i analityczną:

Lp.	Stęż.C2H5OH (%wag.)	Γ2(10^-6mol/m^2) (m. analityczna)	Γ (10^-5 mol/m^2) (m. graficzna)
1	0	0	0
2	10	2,04	1,14
3	20	1,76	0,98
4	30	1,63	0,94
5	40	1,53	0,90
6	50	1,48	0,86
7	60	1,42	0,82
8	70	1,38	0,78
9	80	1,33	0,53

---