Szczecin 27.01.03

Tomasz Klama

Krzysztof Juszczyk

Ćwiczenie 25

Pomiar pH w zastosowaniu do wyznaczania

stałej równowagi reakcji dysocjacji

WPROWADZENIE

W 1909 roku Sorensen za miarę kwasowo-zasadową przyjął ujemny logarytm stężenia jonu wodorowego, nazwał go wykładnikiem wodorowym pH.

pH = - log [H⁺] Powstała w ten sposób skala służąca do ilościowego określania własności kwasowo-zasadowych roztworu.Roztwory kwaśne charakteryzuje stężenie jonu wodorowego ,a zasadowe stężenie jonu wodorotlenowego.Przyjęto, że w roztworach kwaśnych , obojętnych i zasadowych niezależnie od stężenia , iloczyn stężeń jonu H⁺ i OH^- w danej temperaturze jest wielkością stałą. Dla temperatury bliskiej pokojowej przyjęto: [H⁺][OH^-]=10^-14 pH = -log [H⁺] pOH = -log [OH^-] pH + pOH = 14 Roztwór obojętny posiada [H+] = 10-7 , w roztworach kwaśnych [H+]> 10-7 , a zasadowych [H+]< 10^-7, tak więc pH w roztworach wynosi : obojętnym pH = 7 , kwaśnym pH < 7 , a zasadowym pH > 7. W roztworach wodnych słabego kwasu HA ustala się równowaga protolityczna : HA + H₂O ↔ H₃O⁺ + A^- W przypadku , gdy roztwór jest dostateczni rozcieńczony (aktywność wody a_H2O = 1 ) wartość stałej równowagi Ka tej reakcji można przedstawić jako :

Ka=(a_H3O*a_A-)/a_HA (2)

gdzie ai - współczynnik aktywności poszczególnych reagentów.Zlogarytmowanie równania (2) prowadzi do zależności :

logK_a=log_H3O+ +log(a_A-/a_HA) (3)

Po podstawieniu: pH = -log a_H3O+ (4)

pKa = -log Ka (5) a_i = c_i * γ_i (6) gdzie: c_i i γ_i to odpowiednio stężenia i współczynniki aktywności reagentów , otrzymuje się

pH=pK_a+log(C_a/C_HA)+log(γ_A-/γ_HA) (7)

Wprowadzenie do roztworu kwasu HA pewnej ilości soli MA tego kwasu i mocnej zasady , prowadzi do otrzymania roztworu buforowego , którego pH zależy od stosunku stężenia kwasu i soli oraz , w niewielkim stopniu , od współczynników aktywności γ_A- i γ_HA .Można to uzasadnić przyjmując, że sól MA , która jest mocnym elektrolitem , ulega całkowitej dysocjacji . Równocześnie jej obecność wywołuje cofnięcie dysocjacji kwasu HA w reakcji (1) tak, że występuje on wyłącznie w formie niezdysocjowanej, a stężenie jonów A^- pochodzi tylko z dysocjacji soli MA. C_osól = C_M+ = C_A- (8) C_okwas = C_HA (9) Podstawiając zależności (8) i (9) do równania (7) oraz przyjmując , że dla roztworów bardzo rozcieńczonych współczynniki aktywności γ_HA i γ_A- różnią się nieznacznie od jedności, a wtedy

log(γ_A-/γ_A)=0 (10)

otrzymujemy:

pH=pK_C+log(C_0sól/C_0kwas) (11) gdzie Kc jest klasyczną stałą równowagi zdefiniowaną za pomocą stężeń.

Wzór (11) zwany równaniem Hendersona - Hasselbalcha umożliwia ustalenie stosunku stężeń kwasu i soli w roztworze, który musi być zachowany, aby uzyskać wzorcowy roztwór buforowy o określonym pH. Konieczna jest w tym przypadku znajomość stałej dysocjacji.

Roztwory buforowe odznaczają się zdolnością zachowania w dużym stopniu stałości wykładnika jonów wodorowych.. Praktycznie pH roztworów buforowych nie ulega zmianom w wyniku dodania lub odparowania pewnej ilości rozpuszczalnika lub też dodania do roztworu niezbyt dużych ilości kwasu lub zasady.

Niezmienność pH roztworów buforowych obserwuje się tylko w pewnych granicach po przekroczeniu, których roztwór traci swoje buforujące własności. W związku z tym przyjęto stosować termin pojemności buforowej dla ilościowego określenia zmiany pH pod wpływem danej ilości mocnego kwasu lub zasady dodanej do ściśle określonej objętości roztworu buforowego. Miarą pojemności buforowej β jest stosunek dodanej ilości kwasu lub zasady Δb do osiągniętej przez to zmiany pH.

β=Δb/Δ(pH) (13)

Pojemność buforowa mieszaniny buforowej wzrasta wraz ze stężeniem roztworów i maleje wraz z ich rozcieńczeniem .Nie wpływa to w sposób widoczny na zmianę pH, jednak jest niekorzystne z uwagi na zmniejszanie pojemności buforowej roztworu..Wyznaczona z równania (11) klasyczna stała równowagi Kc nie jest identyczna z rzeczywistą stałą równowagi Ka. Chcąc wyznaczyć stałą równowagi Ka należy oprzeć się na równaniu sformułowanym za pomocą aktywności

pH=pK_a+log(a_A-/a_HA)=pK_a+log(C_A/C_HA) (14) Zakłada się przy tym , że współczynnik aktywności części niezdysocjowanej γ _HA jest równy jedności. O wartościach współczynnika aktywności części zdysocjowanej γ_A- decyduje sumaryczna siła jonowa roztworu I zdefiniowana : I=1/2∑c_iz_i (15)

z_i- ładunki jonów występujące w roztworze

c_i- stężenia jonów

Dla stężenia elektrolitów c = 0.001 do 0.01 mol/dm³ współczynnik aktywności jonów można obliczyć :

logγi=-Az²I^-2 (16)

1. stała zależna od stałej dielektrycznej rozpuszczalnika i temp. , dla wody w temp. 25 ^OC A= 0.509 [dm³ ]^1/2 mol ^-1/2

Dla roztworów o stężeniu do 0.1 [mol/dm³ ] log γ_i wynosi:

Log γi=-(Az²I^-2/(1+αβI^-2)) (17)

CEL ĆWICZENIA

Celem jest wyznaczenie stałej równowagi reakcji dysocjacji II stopnia kwasu fosforowego:

H₂PO₄^- ↔ H⁺ + HPO₄ ^2-

W oparciu o oznaczenia pH roztworów buforowych o znanym stosunku stężeń roztworów dwu soli kwasu fosforowego: 1/15 M Na₂HPO₄ i 1/15 M KH₂PO₄ stała równowagi tej reakcji wynosi:

Ka=(a_H+*a_HPO4^2-)/a_H2PO4-=a_H+*(C_HPO4^2-/C_H2PO^4-)(γ_HPO4^2-/γ_H2PO^4-) (20)

W celu określenia stałej równowagi Ka pomiary należy wykonywać dla szeregu roztworów o różnych wartościach stosunku stężeń mniejszych i większych od jedności . Wyznaczona doświadczalnie wartość pH

log(c_Na2HPO4/_CKH2PO4)+log(γ_HPO4^2-/γ_H2PO4)=0 (26)

daje szukaną wartość Ka na podstawie wzoru (25).

pH=pK_a+log(C_Na2HPO4/C_KH2PO4)+log(γ_HPO4^2-/_H2PO4)

POMIARY pH ROZTWORÓW Oznaczenie doświadczalne pH roztworów w ćwiczeniu polega na pomiarach siły elektromotorycznej ogniwa , którym jest elektroda kombinowana. Elektroda ta jest jedno prętowym ogniwem pomiarowym składającym się ze szklanej elektrody wskaźnikowej i chlorosrebrowej elektrody odniesienia umieszczonej w jednej obudowie. W praktyce wyznaczenie pH roztworu badanego wymaga uprzedniego wycechowania układu za pomocą roztworów wzorcowych.

OPRACOWANIE WYNIKÓW

Lp	Na2HPO4	KH2PO4	pH	CH+	CKH2PO4	CNa2HPO4	C1/C2	log(C1/C2)
	cm3	cm3			mol/dm^3	mol/dm^3
1	3	27	5,66	2,1878*10^-6	2,9872	0,3319	0,1111	-0,9542
2	6	24	6,05	8,9125*10^-7	2,6553	0,6638	0,25	-0,6021
3	9	21	6,29	5,1286*10^-7	2,3234	0,9957	0,4286	-0,368
4	12	18	6,48	3,3113*10^-7	1,9915	1,3276	0,6667	-0,1761
5	15	15	6,7	1,9953*10^-7	1,6596	1,6596	1	0
6	18	12	6,83	1,4791*10^-7	1,3276	1,9915	1,5	0,1761
7	21	9	7,02	9,5499*10^-8	0,9957	2,3234	2,3333	0,368
8	24	6	7,23	5,8884*10^-8	0,6638	2,6553	4	0,6021
9	27	3	7,6	2,5119*10^-8	0,3319	2,9872	9	0,9542

Wzór na współczynniki aktywności :
HPO₄^2-i
H₂PO₄^-

log
i=-(Az²_iI^-2)/(1+I^-2) (x)

B=1(mol/dm3)^-1/2

Siła jonowa roztworu I:

I=0,5(C_Na++C_K++C_H2PO4^-+4C_HPO4^2-)

Stężenia poszczególnych jonów wynoszą:

C_Na+=[2a/(a+b)]Co

C_HPO4^2-=[a/(a+b)]Co

C_K+= C_H2PO4^-=[b/(a+b)]Co'

Co i Co'- stężenia początkowe roztworów

a,b - ilość roztworów w mieszaninie w cm3

X=log a/b+logγ_i/γ_k

CNa+	CK+	CHPO4^2-	CH2PO4^-	I	HPO4^2-	H2PO4^2-	log 1/ 2	X
mol/dm^3	mol/dm^3	mol/dm^3	mol/dm^3	mol/dm^3
0,0133	0,06	0,0067	0,06	0,08	0,448	0,112	-0,3522	-1,3064
0,0267	0,0533	0,0133	0,0533	0,0933	0,4755	0,1189	0	-0,6021
0,04	0,0467	0,02	0,0467	0,1067	0,5003	0,1251	0,2341	-0,1339
0,0533	0,04	0,0267	0,04	0,12	0,5228	0,1307	0,4259	0,2499
0,0667	0,0333	0,0333	0,0333	0,1333	0,5435	0,1359	0,6021	0,6021
0,08	0,0267	0,04	0,0267	0,1467	0,5627	0,1407	0,7781	0,9542
0,0933	0,02	0,0467	0,02	0,16	0,5806	0,1451	0,97	1,338
0,1067	0,0133	0,0533	0,0133	0,1733	0,5973	0,1493	1,2041	1,8062
0,12	0,0067	0,06	0,0067	0,1867	0,6130	0,1533	1,5563	2,5105

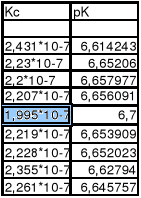
Stała równowagi reakcji dysocjacji I stopnia kw. fosforowego wynosi 1,995*10^-7.

---