Własności jąder atomowych:

1)masa jądra atomowego jest nieznacznie mniejsza od masy odpowiedniego atomu - w jądrze jest skupiona cała masa

2)masa jądra jest (w przybliżeniu) równa całkowitej wielokrotności A masy atomu wodoru i całkowitej wielokrotności A masy protonu, stanowiącego jądro atomu wodoru

(proton poza jądrem jest trwały, neutron nie)

3)liczba masowa A jądra jest liczbą całkowitą najbliższą masie atomowej atomu zawierającego dane jądro

4)ładunek jądra jest równy iloczynowi liczby atomowe Z odpowiedniego atomu oraz ładunku protonu

5)liczba atomowa określa położenie atomu w układzie okresowym pierwiastków

6)pierwiastków jest w przybliżeniu równe 2Z (tylko dla protonu Z=A=1)

7)promień jądra - odległość od środka jądra, na której potencjał działający na cząsteczkę
zaczyna różnić się od potencjału kolumbowskiego)

8)promień jądra (o niewielkim A) jest rzędu 10fm.

9)siły jądrowe mają charakter przyciągający i są krótko-zasięgowe (rzędu 2fm)

10) oddziaływanie jądrowe jest silne w porównaniu z kolumbowskim czy grawitacyjnym (to najsilniejsze oddziaływanie z występujących w przyrodzie)

11)siły jądrowe są niezależne od ładunku elektrycznego, co oznacza, że siła oddziaływania jądrowego między dwoma neutronami jest taka sama jak między dwoma protonami czy między protonem a neutronem

12)jądra atomowe posiadają magnetyczne momenty dipolowe (wynikają one z istnienia wewnętrznych dipolowych momentów magnetycznych protonów protonów neutronów w jądrze oraz z obecności prądów elektrycznych związanych z ruchami protonów wewnątrz jądra.

13)dla wszystkich jąder wartość dipolowego jądrowego momentu magnetycznego
jest rzędu magnetonu jądrowego
(
) gdzie M-masa protonu,
- magneton Bohra

14)znak dipolowego jądrowego momentu magnetycznego może być dodatni lub ujemny

15)dla jąder o parzystych liczbach A i Z magnetyczny moment dipolowy jest równy zeru

16)całkowity moment pędu jądra i zwany jest spinem jądrowym (spin jądrowy jest liczbą całkowita dla jąder o parzystej liczbie A i przyjmuje wartość równą zeru, gdy Z jest również liczbą parzystą). Dla jąder o nieparzystej liczbie A i jest liczbą połówkową (równe całkowitej wielokrotności ½). Liczba kwantowa i określa wartość całkowitego momentu pędu jądra
za pomocą wzoru

17)całkowity moment pędu jądra pochodzi z wewnętrznych spinowych momentów pędu składników jądra - nukleonów oraz z orbitalnych momentów pędu związanych z ich ruchem wewnątrz jądra

Doświadczenie Sterna-Gerlacha - podgrzewali wiązkę i przepuszczali przez pole magnetyczne niejednorodne pole magnetyczne. Spin elektronu
,
spinowa magnetyczna liczba kwantowa.

18)ze spinem jądra wiąże się zagadnienie symetrii funkcji własnych układu dwóch lub więcej identycznych jąder. Funkcje falowe układu identycznych jąder o całkowitej spinowej liczbie i (parzystym A) są symetryczne względem przestawień jąder, czyli są bozonami. Funkcje falowe układu identycznych jąder o połówkowych liczbach i (nieparzystym A) są antysymetryczne, czyli są fermionami.

19)neutron jest cząstką nie naładowaną o podobnej do protonu masie i takim samym wewnętrznym spinowym momencie pędu oraz takich samych własnościach symetrii (
, fermion).

20)jądro o liczbie masowej A i liczbie atomowej Z składa się z A nukleonów w tym Z protonów i A-Z neutronów. Przed odkryciem neutronu przypuszczano, że jądro składa się z A protonów i A-Z elektronów.

21)wiele jąder nie ma kształtu sferycznego, lecz elipsoidalny. Miarą odstępstwa rozkładu ładunków wewnątrz jądra od kształtu sferycznego jest kwadrupolowy moment elektryczny jądra q. Rozkładowi ładunku o kształcie elipsoidy obrotowej wydłużonej w kierunku osi symetrii odpowiadają dodatnie wartości q tym większe im bardziej wydłużona jest elipsoida. Rozkładowi ładunku o kształcie elipsoidy obrotowej spłaszczonej wzdłuż osi symetrii odpowiadają ujemne momenty kwadrupolowe q<0 o tym większej wartości bezwzględnej im bardziej spłaszczona jest elipsoida. Dla jąder o spinie
zdarzają się zarówno jądra o q>0 jak i q<0. Dla jąder o spinach i=0 i
zawsze q=0.

Rozmiary i gęstość jąder

1)rozpraszanie elektronów o energii kinetycznej rzędu kilkuset MeV w cienkich tarczach zawierających wybrane atomy, których jądra są obiektem badań - najdoskonalsza metoda wyznaczania rozmiarów jąder

2)jąder rozpraszaniu decyduje wyłącznie oddziaływanie kolumbowskie elektronów z rozkładem ładunku elektrycznego w jądrze - siły jądrowe nie działają na elektrony.

Przekrój czynny sigma jest miarą prawdopodobieństwa wystąpienia procesu fizycznego

, N- liczba centrów oddziaływania w jednostce objętości
, n - liczba cząstek

jeżeli

jednostki:

(barn)

(femtometry)

Różniczkowy przekrój czynny
(gdy interesuje nas rozkład kątowy zachodzącego procesu)

Zmiana kierunku ruchu elektronów jest skutkiem pojedynczego aktu, podczas którego elekton przebiega bardzo blisko jądra.

Pomiary rozpraszania elektr. Dostarczają inf o rozkładzie ładunku elektrycznego jąder, czyli o ich rozmiarach rozkład ładunku odtwarza rozkład protonów protonów jądrze.

Radialne rozkłady gęstości dają się opisać.

=> za r wstawiamy a-b =>

=>za r wstawiamy a+b =>

gdzie:
zależy od liczby masowej

b=0,55 fm wartość stała

Gęstość ładunku w jądrze jest wew stała i spada gwałtownie do 0 na powierzchni jądra.

Promień a, dla którego gęstość spada do połowy wartości odpowiadającej wnętrzu jądra wzrasta ze wzrostem A.

Grubość warstwy powierzchniowej jądra jest w przybliżeniu określona przez wielkość 2b.

Wartość
wew jądra nieznacznie zmniejsza się ze wzrostem A.

Gęstość ładunku
,określająca rozkład protonów pokrywa się z dokładnością do czynnika proporcjonalnego do Z/A z gęstością masy masy

Spadek
ze wzrostem A wynika ze zmniejszenia się Z/A. Gęstość masy wewnątrz jądra jest jednakowa dla wszystkich jąder.

MASY JĄDER

Dokładne pomiary mas jądrowych dostarczają inf o podst właściwościach jąder .

Metody fizyczne pozwalające wyznaczyć masy jądrowe z wymagana w badaniach dokładnością :-spektroskopia masowa

-bilans energii w reakcjach jądrowych

Odejmując od masy atomu Z masę elektronu wyznaczmy masę jądra atomowego. Równoważnik masowy energii wiązania elektronów w atomach jest tak mały ze można go zaniechać.

FILTR ENERGII(pole elektryczne)

F-siła odśrodkowa

jeżeli odpowiednio dobierzemy r to mamy filtr energii

FILTR PĘDU(pole magnetyczne)

F=nevB ;
;
;
;

FILTR PRĘDKOŚCI(skrzyżowane pole mag i elektr)

neE=nevB

v=E/B

Izotop węgla
przyjęto za wzorzec masy. Węgla
jest bardzo mało/

A,B-jądra

a,b-cząstki

Są to zderzenia niesprężyste, zmienia się masa i energia. Najtrudniej jest otrzymać inf o jądrze B. Jądro A jest najczęściej nieruchome.

Bilans energii w rekcjach jądrowych

Rutkerford dysponował cząstkami

Obowiązuje zasada zachowania ładunku pierwsza sztucznie wywołana reakcja jądrowa..

Zasada zachowanie całkowitej energii relatywistycznej
w laboratorium układzie odniesienia ma postac:

(1)

ponieważ jądro A znajduje się w spoczynku. Zmiana energii kinetycznej Q wynosi

lub
(2)

pomiar Q dla danej reakcji dostarcza inf o masach spoczynkowych obiektów biorących w niej udział. Najtrudniej jest zmierzyć
,wykorzystuje się zasadę zach. pędu do wyeliminowanie tej wartości ze wzoru (1)

W klasycznej granicy mamy:

W przybliżeniu, w którym zaniedbujemy równoważnik masowy, energii wiązania elektronów wzór (2) można zapisać w postaci

gdzie M oznacza masę obojętnych atomów

Masa atomu jest mniejsza od masy jego składników o wielkość
nazywaną niedoborem masy.

Gdy skład swobodnych nukleonów łączy się w jądrach, całkowita energia układu musi zmniejszyć się o wartość
energie wiązania jądra.

ΔMc²=ΔE

1uc²=931,5MeV

Wielkość ΔE/A nazywamy średnią energią wiązania na nukleon.

Dla liczb A ok. 60 mamy najstabilniejsze jądra jak połączymy dwa takie jądra to pojdziemy w stronę stabilnych układów.

Jak rozłączymy ciężkie jądra to tez nam się zrobią bardziej stabilne.

Z synteza do dziś są problemy natury technicznej(bariera kulombowska jest przeszkodą).

A	N	Z	Liczba stabilnych jąder
Parzyste	Parzyste, nieparzyste	Parzyste nieparzyste	166 8
Nieparzyste	Parzyste Nieparzyste	Nieparzyste parzyste	57 53

Przyroda wyraźnie nie lubi nieparzystych (?)

IV Modele jądrowe

a)Model kroplowy

Własności wspólne dla wszystkich jąder:

-gęstość masy wewnątrz jądra nie zależy od rodzaju jądra

-całkowita energia wiązania jara jest proporcjonalna do masy ΔE/A≈const

Własności klasycznej nieściśliwej kropli cieczy:

-gęstość cieczy wewnątrz jest identyczna

-ciepło potrzebne do jej odparowania jest proporcjonalna do masy kropli.

Jądro traktujemy jako kulę, której gęstość jest wewnątrz stała i raptownie spada do zera przekraczaniu powierzchni.

Promień kuli jest proporcjonalny do
a pole powierzchni do
a objętość do A .

Wzór masowy
składa się z sześciu członów

M _Z,A - masa atomu o liczbach Z i A

f₀(Z,A)=1,007825Z+1,008665(A-Z) człon zerowy

1,007825 - masa protonu 1,008665 - masa neutronu

Pozostałe składniki są równoważnikiem masowymi różnych rodzajów energii składających się na całkowitą energię wiązania jądra.

- Przyczynek objętościowy

F₁(Z,A) = -a₁A znak „-” zmniejsza masę jądra, a zwiększa energię

A₁ - pewien współczynnik - może być policzony (jako jedyny)

- Przyczynek powierzchniowy

F₂(Z,A) = a₂A^2/3 zwiększa masę czyli zmniejsza energię.

- Przyczynek kulombowski

f₃(Z,A) = a₃Z²/A^1/3

Uwzględnia on dodatnią energię kulombowksą naładowanego elektrycznie jądra.

- Przyczynek od asymetrii

f₄(Z,A) = a₄(Z-A/2)²/A

Z=N=A-Z

2Z=A

Z=A/2

Obrazuję on dążność jąder do posiadania równej liczby protonów i neutronów.

- Przyczynek po pairingu.

F5(Z,A)={ -f(A) dla Z i N parzystych; 0 dla Z parzystych, N nieparzystych f(A) dla Z i N nieparzystych.

f(A) = a₅A^-1/2

Liczby magiczne

Jądra dla których liczby Z i N przyjmują pewne wyróżnione wartości są nadspodziewanie stabilne.

Te wyróżnione wartości to Z i N zwane liczbami magicznymi są następujące:

2 , 8 , 20 , 28 , 50 , 82 , 126.

Liczbę atomową Z-20 ma 6 izotopów, gdy średnia ich liczba w tym obszarze wynosi ok. dwóch.

Dziesięć izotopów występuje dla Z=50, gdy średnia ich liczba w tym obszarze wynosi ok. 4.

Im bardziej stabilny jest określony rodzaj jądra, tym większa jest częstość jego występowania.

Minimalną energię niezbędna do oderwania od jądra neutronu lub protonu oznaczamy E_n lub E_p i nazywamy energią wiązania ostatniego neutronu lub protonu.

Dla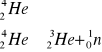
En = 20 MeV (cząstkowy)

(wyrywany neutron)

Ep=19,8MeV

Jądra spontaniczne emitują neutrony:

Dla tych jąder N jest większe o jąder od którejś z liczb magicznych.

b) Jądrowy model gazu Fermiego

Fermiony to cząstki o spinie połówkowym, które podlegają statystyce Fermiego-Diraca.

Nukleon (protony i neutrony) są fermionami.

Zakaz Pauliego.

Założenia modelu:

• każdy nukleon w jądrze porusza się w pewnym wypadkowym potencjale przyciągającym.

• Wypadkowy potencjał ma stałą głębokość wewnątrz jądra.

• Na zewnątrz jądra dąży do zera (w odległości równej zasięgu sił jądrowych)

• W stanie podstawowym jądra nukleonu obsadzają poziomy energetyczne odpowiadającemu wypadkowemu potencjałowi tak, aby bez złamania zakazu Pauliego energia całkowita miała wartość minimalną.

c) Model powłokowy

Szczegółowy opis zachowania się nukleonów w jądrze otrzymamy rozwiązując równanie Schrolingera z elektrycznym potencjałem jądrowym V(r), r - odległość nukleonu od środka jądra funkcje o symetrii sferycznej.

Energia poziomów nukleonu w potencjale V(r), zależy od ich liczb kwantowych n i l - określające radialne i kątowe własności funkcji falowych nukleonu.

Zapełniamy wyznaczone poziomy N neutronami i Z protonami począwszy od najniższego.

Zasada Pauliego ogranicza każdego z poziomów do Z(2l+1) neutronów lub protonów. Obsadzenie takie odpowiada dwu możliwym wartościom liczby kwantowej m_S (określającej kierunek wewnętrznego, spinowego momentu pędu nukleonu) i (2l+1) możliwym wartościom liczby kwantowej m_L (określającej kierunek orbitalnego momentu pędu nukleonu).

Każdy nukleon w jądrze czuje nie tylko efektywny potencjał jądrowy, lecz i silne oddziaływanie spin-orbita proporcjonalnie do S-L (spinowego i orbitalnego momentu pędu nukleonu).

Oddziaływanie spin-orbita ma pochodzenie niemagnetyczne.

Jest pewną cechą sił jądrowych.

W obecności tego oddziaływania m_L i m_S nie są już dobrymi liczbami kwantowymi.

Do numerowania rozczepionych poziomów należy uyć następujących liczb kwantowych n, l, j, m_j. Liczba j określa wartość całkowitego momentu pędu J będącego suma spinowego i orbitalnego momentu pędu nukleonu.

m_j jest liczbą kwantową określającą J_z - składową z całkowitego momentu pędu nukleonu.

Zgodnie z zasadą Pauliego, każdy poziom może pomieść

(2j + 1) nukleonów jednego typu, tyle bowiem różnych wartości moiże przyjmować m_j dla ustawionego j

Cztery liczby kwantowe

N = 1, 2, ... - w przybliżeniu całkowita energia nukleonu na orbicie

l = N (dowolna całkowita liczba nieparzysta) - orbitalny moment pędu (eliptyczność orbity)

j = l ± ½ - całkowity moment pędu (l + spin)

m - wszystkie liczby ułamkowe o mianowniku 2 od -j do +j - przestrzenna orientacja orbity względem dowolnie obranego kierunku

Liczba kwantowa	N = 1	N = 2		N = 3
l = N - 1 N - 3	0	1		2		0
j = l +1/2 l - 1/2	½	3/2	½	5/2	3/2	½
m = j,...,x/2,...,-j	+1/2 -1/2	+3/2 +1/2 -1/2 -3/2	+1/2 -1/2	+5/2 +3/2 +1/2 -1/2 -3/2 -5/2	+3/2 +1/2 -1/2 -3/2	+1/2 -1/2
liczba orbit o danym j	2	4	2	6	4	2
liczba orbit o danym l	2	6		10		2
liczba orbit o danym N	2	6		12

ten model tłumaczy liczby magiczne !!!

Przewidywania modelu powłokowego

1) liczby magiczne

2) całkowity moment pędu prawie wszystkich jąder w stanie podstawowym

3) oddziaływanie dwójkowania

Jeżeli podpowłoka zawiera parzystą liczbe nukleonów, to ich całkowite momenty pędu sprzęgają się parami i przyczynek od tej podpowłoki do całkowitego momentu pedu jądra równy jest zeru.

Dodanie dodatkowego nukleonu do takiej podpowłoki nie ma wpływu na występujące już tam pary.

Całkowity moment pędu jądra o nieparzystym A powinien być równy całkowitemu momentowi pędu jednego, pozbawionego partnera nukleonu w najwyższej, częściowo obsadzonej podpowłoce, czyli wartość spinu jądra powinna być równa liczbie kwantowej j dla danej powłoki.

Jeśli niesparowany nukleon znajduje się na podpowłoce o parzystej liczbie L, to funkcja własna jądra jest parzysta, jeśli L jest nieparzysta, to i funkcja własna jądra jest nieparzysta

d) MODEL KOLEKTYWNY

Dage Bohr - syn Niehlsa Bohra stworzył ten model

Model opiera się na założeniu, że nukleony niezapełnionych powłok jądrowych poruszają się niezależnie od siebie w jądrowym potencjale efektywnym wytwarzanym przez rdzeń jądra zbudowanego z wypełnionych podpowłok.

Potencjał rdzenia nie jest statystycznym potencjałem V(r) o symetrii sferycznej, lecz może ulegać odkształceniom i odpowiadają one kolektywnym ruchom nukleonów rdzenia jądrowego.

Jedną z własności jądrowych, które można wyjaśnić w ramach modelu kolektywnego jest efektywny moment kwadrupolowy q:

Q = ρ[3t² - (x² + y² + t²)]dτ dτ - element objętości

Im większe odchylenie od sferyczności, tym wartość q jest większa

ρ - uśredniona w czasie jądrowa gęstość ładunku

Nazwa modelu	Założenia	Używana teoria
Kroplowy Gazu Fermiego Powłokowy Kolektywny	Jądra mają podobne gęstości a energie wiązania w przybliżeniu proporcjonalne do masy - podobne jak naładowane krople cieczy Nukleony poruszają się niezależnie w potencjale efektywnym Nukleony poruszają się niezależnie w potencjale efektywnym z silnym odwrotnym sprzężeniem spin - orbita Efektywny potencjał jądrowy może ulegać odkształceniom	Klasyczna ( przyczynki od asymetrii wprowadzane bez uzasadnienia) Statystyka kwantowa gazu Fermiego (nukleonów) Równanie Schodinpera z potencjałem efektywnym Równanie Schodinpera z potencjałem efektywnym niesferycznym

Przewidywane własności:

Model kroplowy - poprawne wartości średnich mas i energii wiązania z półempirycznego wzoru masowego

Model gazu Fermiego - głębokość potencjąłu efektywnego jądra, przyczynek od asymetrii

Model kolektywny - magnetyczne momenty dipolowe, elektryczne momenty kwadropolowe

Model powłokowy - liczby magiczne, spiny jądrowe, parzystość

ROZPADY I REAKCJE JĄDROWE

Rozpady jądrowe ( promieniotwórcze) dzielą się na 3 kategorie:

1) rozpady α - spontaniczna emisja cząstek α przez jądra o dużych liczbach atomowych

2) rozpady β - jądra spontanicznie emitują lub absorbują elektrony lub pozytony. Dostarczają informacji o tzw. słabych oddziaływaniach

3) rozpady γ - spontaniczna emisja wysokoenergetycznych fotonów przy przeniesieniu jąder za stanów wzbudzonych do stanu podstawowego

ROZPAD α

Jądra nietrwałe pochodzenia naturalnego są nazywane promieniotwórczymi, a ich procesy rozpadu - promieniotwórczością.

Rozpad α występuje zwykle w jądrach o liczbach atomowych przewyższających 82.

Polega na przemianie niestabilnego jądra na nowe jądro przy jednoczesnej emisji cząstek α

Proces zachodzi samorzutnie, ponieważ jest korzystny energetycznie - masa jądra początkowego jest większa od sumy mas jądra końcowego i cząstki α.

Ubytek masy ( w czasie rozpadu ) wynika ze zmniejszenia się energii kulombowskiej jądra, gdy jego ładunek maleje z Ze o 2e.

Energia wyzwolona w czasie rozpadu jest unoszona w postaci energii kinetycznej cząstki α.

Rozpad α jest efektem kwantowym i polega na przenikaniu cząstki α przez barierę potencjału - efekt tunelowy.

Bariera potencjału jest rezultatem nałożenia się dwu oddziaływań pomiędzy cząstką α i pozostała częścią jądra:

1) oddziaływania jądrowego - przyciągającego i krótko zasięgowego

2) oddziaływania kulombowskiego - odpychającego i długo zasięgowego

Energie rozpadów α są znacznie mniejsze os wysokości bariery równej ok. 30 MeV

rozpad α

Energia wyzwolona w czasie rozpadu jest unoszona w postaci energii kinetycznej cząstki α

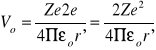
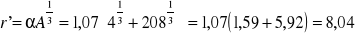
Bariera kulombowska jest jedyną barierą syntezy

r' - suma promieni jądra polonu i cząstki α

Układ zawiera w chwili początkowej wiele jąder tego samego typu, które podlegają rozpadowi.

Nie śledzimy jednego jądra. Bierzemy to statystycznie.

N oznacza liczbę tych jąder, dN<0 liczbę jąder, które ulegają rozpadowi w czasie dt.

Jeżeli R - prawdopodobieństwo rozpadu jednego wybranego jądra w czasie 1s to Rdt - prawdopodobieństwo rozpadu tego jądra w czasie dt, a NRdt - liczba rozpadów w czasie (t,t+dt)

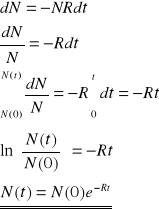
R <- odwrotność czasu, bo wykładnik e musi być bezwymiarowy

N(0) - liczba jąder promieniotwórczych w chwili t=0

N(t) - liczba jąder, które pozostały w układzie w chwili t>0

a tu wykres

(23)strona

Czas relaksacji - czas, po którym wartość spadnie do 1/e.

Czas T, zw. Czasem życia jądra promieniotwórczego jest wielkością charakterystyczną dla danego jądra i danego typu rozkładu.

Jeśli to średni czas istnienia jądra, zanim ulegnie ono rozpadowi

W czasie t, równym czasowi życia T, liczba jąder promieniotwórczych, która nie uległa rozpadowi maleje o czynnik e.

Czas połowicznego rozpadu
jest to czas, w jakim liczba jąder promieniotwórczych danego rodzaju maleje do połowy.

Prawdopodobieństwo rozpadu
bardzo silnie zależy od energii tego rozpadu. Jest ono tym większe im większa jest energia.

Warunek równowagi promieniotwórczej:

Iloczyn liczby jąder i stałej rozpadu jest wartością stałą.

Liczba atomów

Liczba atomów

- powstaje atomów B

- ubywa atomów A

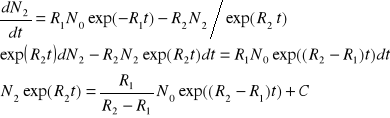
gdy t=0

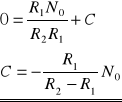
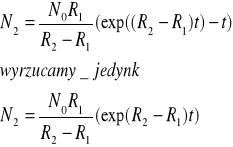
gdy R₂>>R₁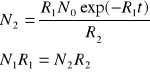

ZADANIE: Oszacowanie Wieku Ziemi

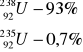
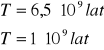
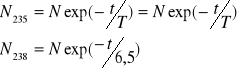
Obecny skład:

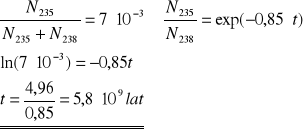
Szeregi promieniotwórcze

W 1903 Ruthenford i Soddy odkryli regułę pozwalającą określić peodukt rozpadu na podstawie znajomości rozpraszającego się pierwiastka i emitowanego promieniowania.

1.Całkowity ładunek elektryczny nie ulega zmianie przy rozpadzie.

2.Suma liczb masowych cząstek początkowych jest równa sumie liczb masowych cząstek końcowych.

Znane są 3 szeregi pierwiastków promieniotwórczych powstające z pewnych pierwiastków macierzystych drogą kolejnych przemian.

Szereg uranu 4n+2

Szereg aktynu 4n+3

Szereg tonu 4n

Każdy szereg kończy się trwałym izotopem ołowiu.

Szereg utworzony wyłącznie z otrzymanych pierwiastków to:

Szereg nept.... 4n+1

Układ zawiera w chwili początkowej wiele jąder tego samego typu, które podlegają rozpadowi.

Nie śledzimy jednego jądra. Bierzemy to statystycznie.

N oznacza liczbę tych jąder, dN<0 liczbę jąder, które ulegają rozpadowi w czasie dt.

Jeżeli R - prawdopodobieństwo rozpadu jednego wybranego jądra w czasie 1s to Rdt - prawdopodobieństwo rozpadu tego jądra w czasie dt, a NRdt - liczba rozpadów w czasie (t,t+dt)

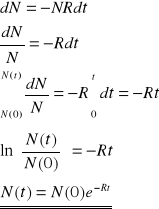
R <- odwrotność czasu, bo wykładnik e musi być bezwymiarowy

N(0) - liczba jąder promieniotwórczych w chwili t=0

N(t) - liczba jąder, które pozostały w układzie w chwili t>0

a tu wykres

(23)strona

Czas relaksacji - czas, po którym wartość spadnie do 1/e.

Czas T, zw. Czasem życia jądra promieniotwórczego jest wielkością charakterystyczną dla danego jądra i danego typu rozkładu.

Jeśli to średni czas istnienia jądra, zanim ulegnie ono rozpadowi

W czasie t, równym czasowi życia T, liczba jąder promieniotwórczych, która nie uległa rozpadowi maleje o czynnik e.

Czas połowicznego rozpadu
jest to czas, w jakim liczba jąder promieniotwórczych danego rodzaju maleje do połowy.

Prawdopodobieństwo rozpadu
bardzo silnie zależy od energii tego rozpadu. Jest ono tym większe im większa jest energia.

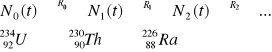
Warunek równowagi promieniotwórczej:

Iloczyn liczby jąder i stałej rozpadu jest wartością stałą.

Liczba atomów

Liczba atomów

- powstaje atomów B

- ubywa atomów A

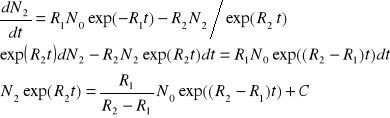
gdy t=0

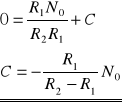
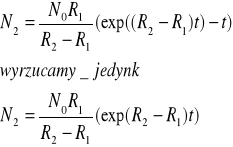
gdy R₂>>R₁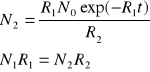

ZADANIE: Oszacowanie Wieku Ziemi

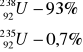
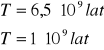
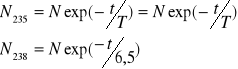
Obecny skład:

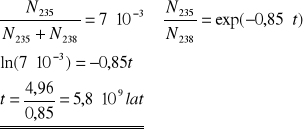
Szeregi promieniotwórcze

W 1903 Ruthenford i Soddy odkryli regułę pozwalającą określić peodukt rozpadu na podstawie znajomości rozpraszającego się pierwiastka i emitowanego promieniowania.

1.Całkowity ładunek elektryczny nie ulega zmianie przy rozpadzie.

2.Suma liczb masowych cząstek początkowych jest równa sumie liczb masowych cząstek końcowych.

Znane są 3 szeregi pierwiastków promieniotwórczych powstające z pewnych pierwiastków macierzystych drogą kolejnych przemian.

Szereg uranu 4n+2

Szereg aktynu 4n+3

Szereg tonu 4n

Każdy szereg kończy się trwałym izotopem ołowiu.

Szereg utworzony wyłącznie z otrzymanych pierwiastków to:

Szereg nept.... 4n+1

Rozpad β

Jądra, których Z różnią się od wartości odpowiadających stabilnym jądrom o tym samym A mogą zmieniać wartość Z w kierunku jąder stabilnych poprzez 3 różne rozpady β:

1) emisja elektronu zachodzi, gdy masa
początkowego jądra jest większa od sumy mas
jądra końcowego i masy spoczynkowej m elektronu.

Energia rozpadu wynosi:

i aby rozpad był możliwy musi energia musi być dodatnia

aby zachodziła emisja.

2) wychwyt elektronu zachodzi, gdy masa
jądra początkowego i masa spoczynkowa elektronu przewyższa masę
jądra końcowego. Energia rozpadu wynosi: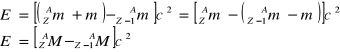

3) emisja pozytonu zachodzi, gdy masa
jądra początkowego przewyższa sumę masy
jądra końcowego i masy spoczynkowej pozytonu m. Energia rozpadu wynosi: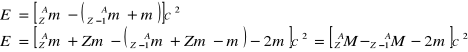

Przy emisji pozytonu atom musi wyemitować elektron, gdyż emitując pozyton jądro zmniejsza swój dodatni ładunek o jeden ładunek elementarny. Pauli w 1931r zapostulował, że emisji elektronu towarzyszy emisja innej cząstki - antyneutrino
. Oddziaływanie tej cząstki z materią jest skrajnie słabe i dlatego nie jest ona wykrywalna w normalnych warunkach. Antyneutrino musi mieć:

1. Ładunek równy zeru

2. Spin s=1/2

3. Zerową masę spoczynkową

Własność 1 zapewnia spełnienie zasady zachowania ładunku elektrycznego przy emisji elektronu

Własność 2 zapewnia spełnienie zasady zachowania momentu pędu elektronu.

Przy emisji pozytonu i wychwycie elektronu emitowana jest cząstka zwana neutrino

Gdzie: e⁺- pozyton

-neutrino

(powyższe oby dwie reakcje formalnie są zgodne)

Neutron się rozpada; proton jest trwały i jego rozpad nie zachodzi

- wychwyt elektronu

Widmo pędowe- funkcja, która określa częstość emisji elektronów o pędzie p_e:

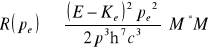
gdzie

-funkcja falowa jądra końcowa

-funkcja falowa jądra początkowa

-parametr

Przejście wzbronione → bardzo małe prawdopodobieństwo takiego przejścia

W przypadku widm atomowych i zamiast
-moment dipolowy

- stanowi miarę liczby stanów kwantowych ,w których może znaleźć się emitowana cząstka - elektron czy antyneutrino

Element macierzowy M. dla rozpadu β zależy od wielkości β i od funkcji
jądra w stanie początkowym i od sprzężonej funkcji
jądra w stanie końcowym. Stanowi on miarę łatwości z jaką jądro przechodzi ze stanu początkowego do końcowego.

Fermi założył, że β jest stałą uniwersalną, zwaną stałą sprzężenia dla rozpadu β.

Rozpad β nie jest skutkiem oddziaływania jądrowego, lecz jest następstwem tzw. słabego oddziaływania

W jądrach stabilnych neutron nie ulega rozpadowi β na proton, ponieważ przeciwdziała temu silne oddziaływanie jądrowe.

Całkując R(p_e) po całym przedziale pędu otrzymamy stałą rozpadu R:

F rośnie ze wzrostem energii kinetycznej K zależność F jest stablicowana

Możemy bardzo precyzyjnie mierzyć energię elektronów i czas życia.

F- funkcja zależna od
lub
(wprost proporcjonalnie)

Jak będziemy umieli wyznaczyć
, to możemy z tych rzeczy wyznaczyć β.

dla

dla

FT nazywamy porównawczym czasem życia, ponieważ zależy ono tylko od stałych uniwersalnych i od wartości jądrowego elementu macierzowego, dostarcza informacji o stanach jądrowych.

Gdy funkcja własna jądra początkowego

pokrywa się z funkcją własną jądra końcowego
to wówczas m'=1

Jeżeli obie funkcje własne nie są identyczne to m' * m' <1

Gdy funkcje własne odpowiadają różnym własnością spinu jądrowego lub\ i mają przeciwną parzystość to: m' * m' = 0.

Reguły wyboru Fermiego

• Δi = 0 zmian spinu

• parzystość jądrowa nie może ulegać zmianie

Reguły wyboru Gamola - Tellera:

• Δi = 0, ± 1 on uwzględnia spin

• parzystość jądrowa nie może ulegać zmianie

Słabe oddziaływania

tryt
hel

Wartość FT jest dla tego rozpadu bardzo mała.

Wartość m' = 1

Stanom podstawowym obu jąder odpowiada spin jądrowy i = ½ i całkowita funkcja własna parzysta.

Funkcja falowa jest niemianowaną ale tam jest element objętości

- objętość jądra

Rodzaj oddziaływania	Energia	Zasięg
Oddziaływanie stałe		bardzo krótki
Oddziaływanie silne		krótki
Oddziaływanie elektromagnetyczne		duży(1/r)
Oddziaływanie grawitacyjne		duży(1/r)

W 1956 Reines i Cowan odkryli antyneutrino wykorzystując rekacje:

asymetria emitowanych elektronów jest to cecha charakterystyczna dla oddziaływania stałego.

Wu stwierdziła, że elektrony emitowane są niesymetryczne względem płaszczyzny prądu kołowego.

Opis rozpadu β nie jest identyczny z opisem jego odbicia zwierciadlanego.

Rozpad β nie jest niezmienniczy względem inwersji przestrzennej albo parzystość nie jest zachowana w stałych oddziaływaniach.

Spiralność

Spinowy moment pędu antyneutrina jest zawsze równoległy do kierunku pędu - spiralność prawoskrętna.

Neutrino ma spiralność lewoskrętną.

Rozpad gamma.

W tych rozpadach nadmiar energii jader przy przechodzeniu od wzbudzonych do stanow o nizszej energii unoszony jest przez promieniowanie elektromagnetyczne.

Kwant gamma emitowany z jadra charakteryzuje się:

-energia jaka unosi z jadra Egamma=Ef-Ei

-moment pedu L jaki unosi z jadra

w zaleznosci od L mowimy o multipolowosci przejscia, L może przyjmowac wartosci 1,2,3..

okresla ona multipolowosc zarówno elektrycznych jak i magnetycznych L=1 dla przejsc dipolowych, L=2 kwadrupolowych, L=3 oktupolowych

Reguły wyboru dla przejsc elektrycznych:

-

-dla L nieparzystych parzystosc jadrowa ulega zmianie

-dla L parzystych jest niezmieniona

Reguły wyboru dla przejsc magnetycznych:

-

-dla L parzystych parzystosc jadrowa ulega zmianie

-dla L nieparzystych pozostaje niezmieniona

i=3 i=2 |ii-if|=1 E1-przejscie elektryczne dipolowe

i=2 i=0 |ii-if|=2 E2-przejscie elektryczne kwadrupolowe

jeżeli wartosc L jest nieparzysta, a stan poczatkowy i koncowy roznia się parzystoscia, to przejscie charakter ma elektryczny. Zas przy jednakowej parzystosci obu stanow ma charakter magnetyczny.

Jeżeli wartosc L jest parzysta to przejsciu elektrycznemu odpowiada jednakowa parzystosc przed i po emisji, zas przejscie magnetyczne zachodzi ze zmiana parzystosci jadrowej.

Prwdopodobienstwo przejscia gamma silnie zalezy od energii E gamma i multipolowosci L. Rosnie ono silnie ze wzrostem E gamma a silnie maleje ze wzrostem L.

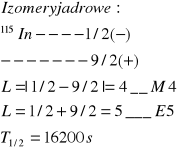
Γ-szerokosc w polowie wysokosci

Zjawisko konwersji wewnetrznej-energia jadra jest przekazywana elektronom.

Jest to przejscie w którym jadro przekazuje swoja energie bezposrednio jednemu z elektronow powloki atomowej. Elektron unosi energie moment pedu i parzystosc przejscia jadrowego podobnie jak kwant gamma.

Poniewz jeden elektron unosi cala energie przejscia to widmo elektronow konwersji wewnetrznej jest dyskretne w odroznieniu widma ciaglego elektronow pochodzacych z rozpadu beta.

Współczynnik konwersji wewnetrznej:

zalezy od energii przejscia, multipolowosci

Rt-calkowite prawdopodobienstwo

α-suma stosunkow prawdopodobienstw emisji z roznych powlok

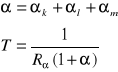
T-czas po jakim po jakim zachodzi dany proces od wzbudzenia jadra

Czas zycia stanu wzbudzonego wyrazany jest często za posrednictwem szerokosci i poziomu. Jeżeli jadro przebywa srednio w stanie wzbudzonym przez skonczony czas T , rowny czasowi bycia tego stanu, to energia tego stanu nie moze być okreslona scisle
.

Reakcje jadrowe.

W kazdej reakcji jadrowej musza być zachowane wielkosci:

-calkowita energia relatywistyczna

-ped

-moment pedu

-ładunek

-parzystosc

-liczba nukleonow

kazde stabilne jadro może być zarówno czastka padajaca jak i tarcza. W reakcjach jadrowych mogą powstawac rozmaite czastki. Jadra koncowe mogą być stabilne i niestabilne.

Celem zadania reakcji jadrowych jest:

-poznanie mechanizmu reakcji

-poznanie budowy jadra atomowego i struktury jego stanow wzbudzonych

Z reguly czastki oddzialujace z jadrem silami jadrowymi i wywolujace reakcje sa naladowane dodatnio .

Neutrony pozbawione ladunku elektrycznego nie oddzialywuja kulombowsko z jadrem. Brak bariery kulombowskiej powoduje ze nawet bardzo powolne neutrony mogą oddzialywac z jadrem.

Brak stron 37-41

Nie jest możliwe podtrzymanie tej reakcji.

K_∞-dotyczy materiału nieskończenie dużego; rozmiary krytyczne - nie zajdzie w nich samoistnie reakcja łańcuchowa.

Powyżej rozmiarów krytycznych K jest większe od jedności i ilości neutronów wykładniczo rośnie w czasie.

Przy rozmiarach krytycznych K=1 i ilość neutronów jest stała. Poniżej rozmiarów krytycznych K<1 i ilość neutronów wykładniczo maleje w czasie

²³⁵U- jest go bardzo mało, poniżej 1%

Każda absorpcja neutronu przy ²³⁵U powoduje rozczepienie.

Każde jądro ulega rozczepieniu przy pochłonięciu neutronu.

K_∞-2,5

W uranie naturalnym (99,3%-²³⁸U i 0,7% - ²³⁵U) nie może powstać reakcja łańcuchowa.

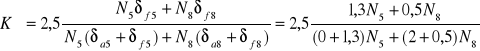
N₅ - ²³⁵U N₈ - ²³⁸U

W wyniku rozczepienia powstają neutrony o energii ~ 2MeV, bardzo szybkie.

Kładąc K_∞ =1

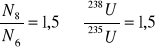
40% ²³⁵U 60% ²³⁸U

Przy składzie izotopowym rzeczywistym:

dla wolnych neutronów

Dlatego są moderatory:

1. przekrój czynny ²³⁸U na chwytanie neutronów powolnych

2. przekrój czynny na rozczepienie ²³⁵U przez neutrony powolne przy zależności
   

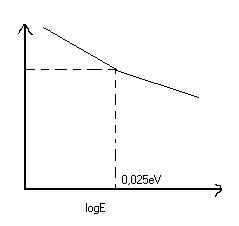
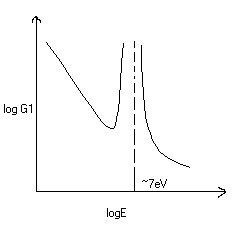
a) b)

Rdzenie reaktorów jądrowych stanowią charakterystyczne regularne siatki elementów paliwowych otoczonych moderatorem (w celu spowolnienie neutronów)

Ciepło wytworzone podczas rozczepienie usuwane jest przez chłodziwo opływające gorące elementy

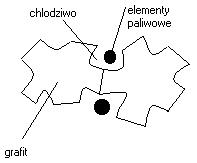
Równoważnik dawki to iloczyn dawki pochłoniętej ??? ???

1ren = 1 rad * QF

SYNTEZA JĄDROWA

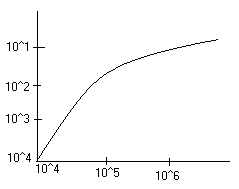
Przekrój czynny na reakcję

Pochodzenie pierwiastków

Cykl protonowy

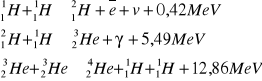
Jak się połączą 2 jądra helu

Z małym prawdopodobieństwem, bo trzeba pokonać barierę kulombowską.

Cykl węglowy:

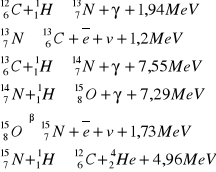
Węgiel jest katalizatorem. Wyprodukowaliśmy energię.

Pierwiastki cięższe od żelaza nie powstają w reakcjach syntezy gdyż ich liczby A mają wartość większą od 60. Jądra az do
powstają przez cykle kolejnych wychwytów neutronów i rozpadów
.

Siły jądrowe (nukleonowe)

1. siły nukleonowe są silne

2. siły nukleonowe są krótkozasięgowe

3. siły nukleonowe są przyciągające

4. siły nukleonowe są niezależne od ładunku

5. siły nukleonowe są ??? ??? się.

Zd3. Jest rdzeń odpychający; do pewnej wartości są przyciągające, a potem odpychają

Deuteron

Energi wiązania : deltaE=2,22MeV

Spin jądrowy: i=1

Parzystość jądrowa: parzysty

Magnetyczny moment dipolowy :

elektryczny moment kwadrupolowy:

Promień, przy którym gęstość ładunku spada do połowy a = 2,1 fm

Deuteron ma różny od zera elektryczny moment kwadrupolowy z czego wynika że rozkład gęstości prawdopodobieństwa nie ma symetrii sferycznej. Zatem potencjał nukleonowy, który określa siłę oddziaływania obu nukleonów również nie ma symetrii sferycznej.

Dla każdego potencjału o symetrii sferycznej funkcja własna stanu podstawowego odpowiada liczbie kwantowej l = 0

Miarą odstępstwa od symetrii sferycznej jest wielkość q/r¹² która dla deuteronu wynosi zaledwie 2,7*10^-31 / 4,41*10^-30 = 6%

Okazuje się że można odtworzyć zmierzoną wartość elektrycznego momentu kwadrupolowego, jeżeli przyjmie się że przez 96% czasu deuteron znajduje się w stanie l=0, a przez pozostały czas w stanie l=2

Stan złozony jest jako całosc parzysty ponieważ oba stany składowe sa parzyste

l=0 l=2

s=1 j=1 s=1

j=1

³S₁

³D₁

Górny wskaźnik oznacza 2s+1, litera oznacza wartość l (s dla l=0 D dla l=2) dolny wskaźnik oznacza wartość j.

Deuteron można traktować jako układ, w którym nukleony są związane w stanie ³S₁ odpowiadającym sferyczn...(brak tekstu)

Informacji o potencjale dostrczaja:

-energia wiązania stanu podstawowego 2,22MeV

-funkcji własnej stanu podstawowego musi odpowiadać gęstość ładunku malejąca w odległości 2,1 fm do połowy swojej wartości w początku układu

(miejsce na rysunek)

(miejsce na 2 rysunki)

siła centralna nie zależy od odległości

siła nie zależy tylko od odległości, ale od wzajemnego ustawienia jest to siła tensorowa

siły tensorowe i siły spinowo orbitalne (miejsce na dużo rysunków)

IZOSPIN

Pojęcie izospinu jest pojęciem czysto matematycznym. Jest używane do identyfikacji stanów klasycznych tzw. izobarów czyli układów o identycznych liczbach A nukleonów.

dineutron

deuteron

diproton

s=0 T=1

s=1 T=0

T_z=-1 T_z=0 T_z=1

Zgodnie z zakazem Pauliego tylko deuteron ma poziom s=1 odpowiadający trypletowi spinowemu i odpowiada mu stan związany.

Singletowi spinowemu s=0 odpowiada stan niezwiązany

Dla A=2 najniższy poziom nazywamy singletem izospinowym i oznaczamy T=0 Trzy wyższe poziomy tworzą tryplet izospinowy T=1

Składową T_z wyznaczamy ze wzoru

w ogólnym przypadku dla ustalonego T składowa T_z przyjmuje wartości: -T, -T+1,...,T-1,T

T_z=1/2 dla protonu T_z=-1/2 dla neutronu

Pojedynczemu nukleonowi przypisuje się T=1/2, co odpowiada dwu możliwym wartościom T_z=1/2 i T_z=-1/2 zatem izospin pozwala mówić o neutronie i protonie.

Strony 52-56

Z tej masy wynika krótki zasięg sił jądrowych

masa spoczynkowa
140 MeV/

masa spoczynkowa
135 MeV/

n
,

p
,

n
,

p
,

p
,

n
,

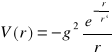
potencjał

17.5.2005

piony są bozonami (s=0,1,2,3...)

wszystkie piony mają spin d=0

Piony
można traktować jako stan trypletowy pionu 0 izospinie T=1

dla nukleonów
(ładunek)

dla nukleonów
Q=0

dla nukleonów
Q=1

dla pionów

dla nukleonów i pionów

B- liczba bozonowa, równa 1 dla nukleonów

0 dla pionów

czas życia ~

~

~

- mion dodatni , mezon

- netrinum mionowe

-ujemny mezon

czas który charakteryzuje oddziaływania

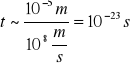
Miony

Zostały odkryte w 1936r przez Andesona i Neddermayera w promieniowaniu kosmicznym

Piony są ściśle związane z nukleonów i uczestniczą u silnych oddziaływaniach.

Miony są ściśle związane z elektronami i biorą udział w słabych oddziaływaniach.

~10
(oddziaływanie słabe)

miony i neutrinina są fermionami - powstają i zanikają parami - cząstka antycząstka

Mion, elektron mertrina mionowa elektronowe praz wszystkie odpadanie antycząstek noszą wspólną nazwę Leptonów (to są cząstki punktowe (naprawdę eleneutronowa))

Liczba Leptonów w układzie izolowanym pozostaje stała

Rysunek

Mezon K

dodatnio naładowane

obojętne

są bozonami o spinie ) i ujemnej wewnętrznej parzystości

Masy spoczynkowe wynoszą:

Jednocześnie z mezonami K powstają cząstka

Mezon K powstały w oddziaływaniach silnych zawsze parami

Bazon oznacza cząstkę, kóra uczestniczy w silnych oddziaływaniach i której masa spoczynkowa jest co najmniej równa masie spoczynkowej nukleonu

Prawo zachowania liczby bozonowej EB=const

+1 dla nukleonów

-1 dla antycząsteczek

Mezon K rozpadają się na wiele różnych sposobów

Produktami rozpadów są piony i w niektórych przypadkach leptony

jest również cząstką nietrwałą sposoby rozpadu to:

..........

Q=Tz+B/2 (dla nukleonów i pionów)

Q=Tz+B/2-1/2 dla

Q=Tz+B/2+1/2 dla

Q=Tz+B/2-1/2 dla

B wynosi o dla pionów, 1 dla nukleonów i -1 dla antynukleonów

B wynosi +1 dla bozonów -1 dla antybozonów 0 dla mezonów

S- liczba kwantowa zwana dziwnością -> 0 gdy cząstki są nie dziwne

gdzie s=0 dla nukleonów i pionów

s=-1 dla

s=1 dla

W silnych oddziaływaniach zachowane izospin T i dziwność S.

Lepyony - cząstki o masach z przedziału 0-130MeV/c
(neutrina, elektron,mion)

Bozon to są cząstki, które przenoszą oddziaływania!!!

---