1.równanie naturalne klotoidy rys

LR=a² F=mV²/R, k=1/R, F=mV²k, Q=mg, tgα=h/b, tgα=F/Q, h/b= F/Q, h=(bmV²k)/mg=b(V²k/g)

Wartość przechyłki h wyprowadza się stopniowo:

h=iL, (bV²k)/g=iL, L=(bV²/gi)k, gdzie bV²/gi=a² , LR=a²

L-dł. klotoidy mierzona od punktu styczności osi drogi z klotoidą R-promień krzywizny w końcu odcinka L, a²-współcz. proporcjonalności, Q-siła ciężkości, F-siła pociągowa skierowana wzdłuż kierunku jazdy, h-przechyłka

2. analiza dokł. tyczenia lokalizującego - podst. teoretyczne z uwzględnieniem i bez błędności p-któw nawiązania 

Przedmiotem tyczenia lokalizującego jest określenie położenia względem osnowy realizacyjnej elementów projektowanego obiektuoraz oznaczenie ich w terenie w taki sposób aby wytyczane punkty mogły być wykorzystane po wykonaniu robót budowlano-motażowych.

Metoda biegunowa. Stabilizujemy w terenie dwa punkty A, B tworzące bazę i odkładając w terenie od tej osnowy dany kąt i odległość otrzymujemy punkt do wyniesienia. Na dokładność tyczenia mają wpływ:niedokładność osnowy, niedokł. wyzn. punktu osnowy, niedokł. czynności pomiarowych (centr. instrumentu 0,7(L/C)*e, odłożenie kąta:L(m_α/ρ), odłożenie odległości:m_L), niedokładność utrwalenia:

m_og²=Σ⁴_i=3m_i²-uwzględnienie błędów osnowy

m_wewn²=Σ⁴_i=3m_i²-wewn. błąd tyczenia

Analiza dokładności: m_p=√(m_x²+m_y²), Korzystając ze wzorów na wsp. punktu P X_p=X_A+cosαd, Y_p=Y_A+sinαd i różniczkując je otrzymujemy wzory na błąd położenia punktu P: m_x²=[(δ_Xp/δα)m_α]²+[(δ_Xp/δd)m_d]²,

m_y²=[(δ_Yp/δα)m_α]²+[(δ_Yp/δd)m_d]²,

m_x²=(-sinαd m_α)²+(cosα m_d)²,

m_y²=(cosαd m_α)²+(sinα m_d)²,

m_p²= m_α²d²+m_d²

Błąd długości:

d_A-P=√ (X_P-X_A)²+(Y_P-Y_A)²

m_d²=(∂d/∂X_P*m_XP)²+(∂d/∂X_A*m_XA)²+(∂d/∂Y_P*m_YP)²+(∂d/∂Y_A*m_YA)², gdzie:

∂d/∂X_P=(X_P-X_A)/√[(X_P-X_A)²+(Y_P-Y_A)² ]

∂d/∂X_A=-(X_P-X_A)/√[(X_P-X_A)²+(Y_P-Y_A)² ]

∂d/∂Y_P=(Y_P-Y_A)/√[(X_P-X_A)²+(Y_P- Y_A)² ]

∂d/∂Y_A=-(Y_P-Y_A)/√[(X_P-X_A)²+(Y_P-Y_A)² ]

Błąd kąta można wyzn. ze wzoru: m_α/ρ=m_d/d

3. poszerzenie osi torów kolejowych

Dane: R≥V², e-z proj.

L=AO₂=√(O₁O₂)-(AO₁)²; O₁O₂=2R; AO₁=R+(R-e); L=√4R²-4R²+4Re-e²; L=√4Re-e² RYS.

Punkt T₃ ustala się na podst. miar podanych na projekcie, natomiast T₁ znajdziemy przez odłożenie L wzdłuż toru 2. Pozostałe punkty znajdziemy w oparciu o α. Porównując równania: tgα=L/(2R-e), tgα=e/(L-2t)otrzymujemy t=(L²+e²)/4e, t=(L²+e²)/4e≈L/4

Punkty pośrednie otrzymamy ze wzoru:y_i=x_i²/2R, podstawiając za R≈L²/4e:y_i=(2e/L²)x_i².

4. przemieszczenie bezwzględne budowli - podst. Teoretyczne

Przemieszczenie bezwzględne punktu-zmiana położenia punktu zaistniała w rozpatrywanym okresie czasu i wyrażona przez wektor przemieszczenia w stałym układzie odniesienia (układ współrzędnych, w którym wyrażone są przemieszczenia punktów i obiektów, wyznaczony przez zastabilizowane punkty sieci kontrolnej zidentyfikowane jako stałe)

Przemieszczenie obiektu-zmiana położenia obiektu, polegająca na przesunięciu albo na obrocie lub przesunięciu i obrocie, przy której wzajemne odległości wszystkich punktów odległości nie ulegają zmianie.

Pomiar przemieszczenia to prace projektowe, obliczeniowe, pomiarowe do określenia:wektora zmian położenia obserwowanych punktów reprezentujących badany obiekt.

Obserwacje wybranych punktów w ustalonych interwałach czasowych,

T_o-pomiar wyjściowy

T_a-pomiar aktualny

U_P=U_PT-U_Pφ+U_Pε

T-translacja, φ-skręt, ε-odkształcenie

Wyznaczenie przemieszczeń bezwzględnych:sieć punktów odniesienia założonych poza siecią oddziaływania obiektu na otoczenie

1)obiekt iżynierski

RYS

2)powierzchnia terenu

RYS

Przy dużej ilości punktów kontrolowanych umieszczonych na badanym obiekcie wygodniej jest oddzielnie wyznaczyć przemieszczenia punktów kontrolowanych i oddzielnie stanowisk obserwacyjnych. Postępowanie takie polega na wyodrębnieniu z całej sieci

a)sieć punktów odniesienia

b)konstrukcji wyznaczających X, Y punktów kontrolowanych a następnie:

1)wyzn. przemieszczeń stanowisk obserwacyjnych przy założeniu punktów odniesienia

2)obliczenie poprawek do aktualnych obserwacji (kierunki, kąty, boki) ze względu na przemieszczenia stanowisk obserwacyjnych

3)wyznaczenie składowych przemieszczeń punktów kontrolowanych na podstawie skorygowanych wartości obserwacji aktualnych i wyjściowych

5. badanie pionowości budowli wysokich - met. kątowa wzór, rys., metody opracowania wyników

Pomiar polega na wyznaczeniu kierunków stycznych (lewej K_L i prawej K_P) do obiektu w każdym z przekroju, z każdego stanowiska obserwacyjnego.

Średnia z każdej pary kierunków określa położenie osi budowli w poszczególnych przekrojach:

K=(Kl+KP)/2

Natomiast ΔKi=Ki-K1 jest różnicą między położeniem osi na poziomie i oraz na poziomie najniższym - najbliższym podstawie budowli ( przyjmowany za poziom zerowy) i pozwala z zależności ui=(ΔKi/ρ)d

d - odległość między stanowiskiem a osią obiektuobliczyć składowe wychylenia osi budowli od pionowości w kierunku prostopadłym do celowych z poszczególnych stanowisk obserwacyjnych

RYS

Liczba stanowisk od 2 do 5, najlepiej 3, a kąt między poszczególnymi stanowiskami a kierunkiem do osi obiektu 2Π/n, n - liczba stanowisk obserwacyjnych.

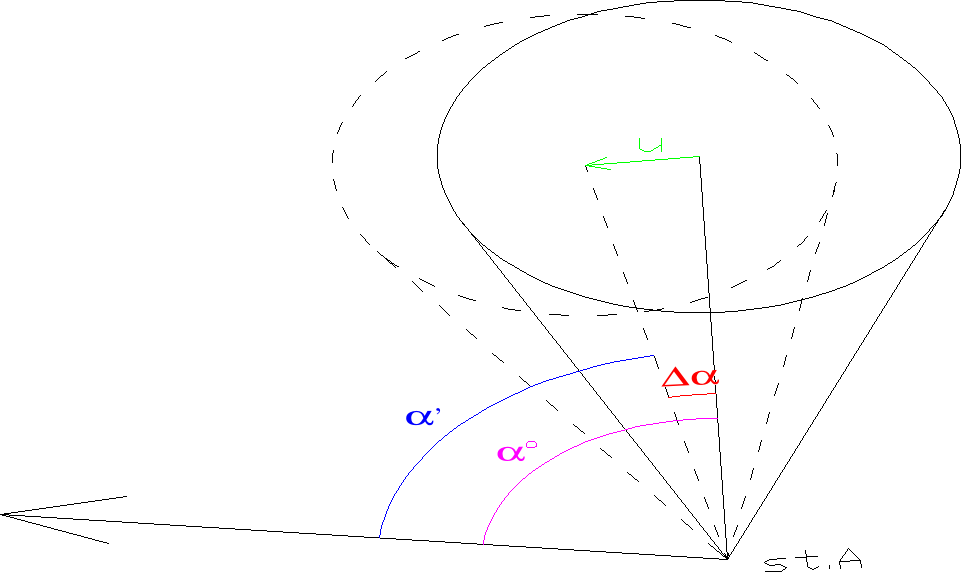
α⁰ - kąt miedzy kierunkiem nawiązania a osią obiektu tuż przy podstawie(poziom zerowy)

αⁱ - kąt między kierunkiem nawiązania a osią budynku na danym poziomie

u=d(Δα/ρ'')=d((α0-αi)/ρ”)

mu²=(du/dd)²md²+(du/dα0)²mα0²+(du/dαi)²mαi²

du/dd= Δα/ρ''

du/dα0=d/ ρ

du/dαi =- d/ ρ

mα= mα0= mαi

u=u√(md/d)²+2(mα/Δα)²

mu=u(mα/Δα) √2

(md/d)² - jest bardzo małe i pomijamy

---