[DM 01]

[1/01] Stosując indukcję:

(1) wykaż poprawność wzorów na sumę szeregu arytmetycznego i geometrycznego.

(2) wykaż, że n ∈ N ⇒ 6 | n(n + 1)(2n + 1) (a | b czytaj "a dzieli b" lub "b jest podzielne przez a")

(3) wykaż, że n ∈ NP ⇒ 4 | 1 + 3ⁿ (NP - zbiór naturalnych liczb nieparzystych)

(4) wykaż, że n ∈ NP ⇒ 5 | 2ⁿ + 3ⁿ

(5) wykaż, że jeżeli wyrazy ciągu a_n spełniają warunki: a₁ = 1, a₂ = 2, a_n = a_n-1 + a_n-2, to a_n < (7/4)ⁿ.

(6) wykaż, że jeżeli wyrazy ciągu a_n spełniają warunek: a_n = a_n-1 / (2a_n-1 + 1), to a_n = a₀ / (2na₀ + 1).

(7) wykaż, że m⁵ / 5 + m³ / 3 + 7m / 15 jest liczbą całkowitą dla każdego całkowitego m.

[2/01] Dowieść, że dla dodatnich, rzeczywistych a₁,...,a_n mamy:

• a_n/a₁+a_i / a_i+1 ≥ n,

• jeżeli a₁...a_n = 1, to ≥ n,

• zawsze (a₁...a_n)^1/n ≤ (a₁+...+a_n)/n. Kiedy zachodzi równość?

[3/01]

const

k = ...;

type

T = array[1..k] of integer;

for i = 1 to k - 1 do

if T[i] < T[i+1] then "zamień T[i] z T[i + 1]"

writeln(T[k]);

Udowodnij, że powyższy algorytm w pseudo-pascalu wypisuje maksymalną wartość tablicy T. (Wskazówka: Zastosuj indukcję względem i. Zastosuj predykat P(i) ⇔ "po wykonaniu i - tego kroku pętli element maksymalny znajduje się w polu tablicy o indeksie większym niż i").

[4/01]

const

k = ...;

type

T = array[1..k] of integer;

for i = 1 to k - 1 do

for j = 1 to k - i do

if T[j] < T[j+1] then "zamień T[j] z T[j + 1]"

Udowodnij, że powyższy algorytm w pseudo-pascalu sortuje tablicę T. (Wskazówka: Zastosuj indukcję względem i. Skorzystaj z zadnia poprzedniego. Określ wyraźnie predykat P, który występuje w Twoim dowodzie (zapewne inny niż w poprzednim zadaniu)).

[5/01] W mieście Skrzyżne nie ma ślepych ulic (tzn. jadąc dowolną ulicą w dowolnym kierunku zawsze dojedziemy do skrzyżowania) i wszystkie ulice są dwukierunkowe. Do każdego skrzyżowania dochodzi parzysta liczba ulic. Z każdego skrzyżowania można dojechać do każdego innego skrzyżowania. Udowodnij, że można w tym mieście przejechać wszystkie ulice tak, aby każdą ulicą jechać tylko jeden raz, rozpoczynając i kończąc podróż na tym samym skrzyżowaniu. (Wskazówka: zastosuj indukcję względem liczby ulic. Skorzystaj z silniejszej wersji zasady indukcji matematycznej (krok indukcyjny: [P(s) ∧ P(s + 1) ∧ ... ∧ P(n)] → P(n + 1)).

[6/01] Pokaż, że dla dowolnej liczby naturalnej n istnieje liczba naturalna c_n taka, że jeżeli połączymy odcinkami każde dwa wierzchołki k-kąta foremnego, gdzie k ≥ c_n, to przy dowolnym pokolorowaniu wszystkich tych odcinków n kolorami pewne trzy odcinki będące bokami jednego trójkąta uzyskają ten sam kolor.

[7/01] Które z poniższych implikacji logicznych są prawdziwe. Dla każdej nieprawdziwej implikacji przedstaw kontrprzykład dokładnie definiując predykat P.

• [P(1) ∧ ∀_n∈N(P(n²) → P(n² + 1)) ∧ ∀_n∈N(P(n + 1) → P(n))] ⇒ ∀_n∈N(P(n))

• [P(125) ∧ ∀_n∈N(P(n²) → P(n² + 2n + 2)) ∧ ∀_n∈N(P(n + 1) → P(n))] ⇒ ∀_n∈N(P(n))

[8/01]

(a) Udowodnij, że poniższy program wypisuje wyłącznie liczby całkowite.

x := 1;

while (1 < 2) do

begin

writeln(x);

x :=
;

end;

(b) Udowodnij, że następujący program wypisuje wyłącznie liczby całkowite.

x = 1;

while (1 > 0)

{

print(x);

}

[9/01] Dany jest ciąg określony rekurencyjnie:

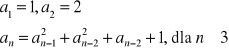
Udowodnij, że ~∃_n∈N (3 | a_n).

[10/01] Dany jest ciąg określony rekurencyjnie:

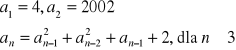
Udowodnij, że ∀_n∈N (4 | (a_n + 1)² - 1).

[11/01] Ciąg a_n określony jest rekurencyjnie:

a₁ = 1, a₂ = 1,

a_n+2 = a_n+1 + a_n, dla n ∈ N.

Udowodnij, że ∀_n∈N(5 | a_5n).

---