Kowariancja:
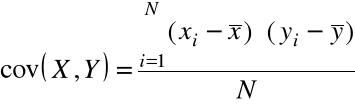
Współczynnik korelacji liniowej Pearsona:
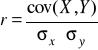
Ostatecznie otrzymujemy:
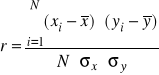
Po pewnych przekształceniach wzór ma postać:
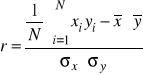
Przykład:
W celu ustalenia, jaka jest zależność stopnia zużycia maszyn od okresu ich użytkowania zebrano dane dotyczące 15 maszyn w pewnej fabryce:
Nr maszyny |
Okres eksploatacji w latach |
Stopień zużycia w % |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
7 2 6 9 2 4 3 1 11 10 4 8 5 2 1 |
27 6 28 33 8 12 12 8 45 40 13 32 17 10 9 |
Ustal siłę zależności między tymi cechami.
Rozwiązanie:
Ustalamy, która zmienna jest zależna (Y), a która niezależna (X).
Rysujemy korelacyjny diagram rozrzutu:
Nr maszyny |
Okres eksploatacji w latach (xi) |
Stopień zużycia w % (yi) |
x2 |
y2 |
x*y |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
7 2 6 9 2 4 3 1 11 10 4 8 5 2 1 |
27 6 28 33 8 12 12 8 45 40 13 32 17 10 9 |
49 4 36 81 4 16 9 1 121 100 16 64 25 4 1 |
729 36 784 1089 64 144 144 64 2025 1600 169 1024 289 100 81 |
189 12 168 297 16 48 36 8 495 400 52 256 85 20 9 |
Ogółem |
75 |
300 |
531 |
8342 |
2091 |
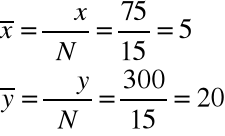
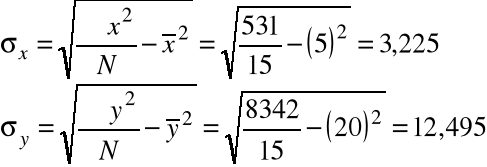
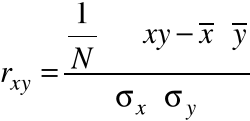
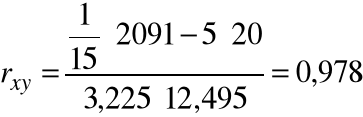
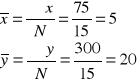
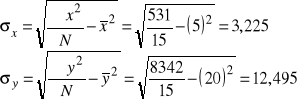
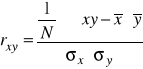
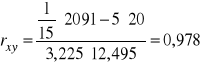
Wyszukiwarka
Podobne podstrony:
zadania-ćw.2, WSFIZ B-stok, statystyka opisowa
projekt , WSFIZ B-stok, statystyka opisowa
wyk3st, WSFIZ B-stok, statystyka opisowa
statystyka-dd, WSFIZ B-stok, statystyka opisowa
stat-zal, WSFIZ B-stok, statystyka opisowa
Wykład 7 Kowariancja i korelacja, Statystyka opisowa
STATYSTYKA OPISOWA '
1 Statystyka opisowa Wprowadze Nieznany (2)
Gorgol I Elementy statystyki opisowej
STRUKTURA DEMOGRAFICZNA I EKONOMICZNA, WSFIZ B-stok, geografia ekonomiczna
egzamin ze statystyki, Statystyka opisowa
ROZDZIAŁ 4, Statystyka opisowa
Parametry stosowane w statystyce opisowej, Płyta farmacja Bydgoszcz, statystyka, pozostałe
więcej podobnych podstron