Nagrzewanie toru pršdowego w próżniowych komorach gaszeniowych łšczników

Andrzej Purczyński

Rozwišzanie ogólne

Do częœci toru pršdowego zamkniętej w komorze gaszeniowej nie ma zwykle dostępu i ocena temperatury elementów tego toru jest utrudniona. Na podstawie pomiarów temperatury częœci zewnętrznych komory i danych jej budowy, można jednak oszacować spodziewanš wartoœć temperatury elementów zamkniętych wewnštrz komory.
Obliczenia można wykonać posługujšc się metodami analitycznymi albo numerycznymi. Przy założeniu uproszczonego modelu komory, przedstawionego na rysunku, można wyznaczyć rozkład temperatury T(x) rozwišzujšc równanie bilansu cieplnego dla stanu cieplnie ustalonego.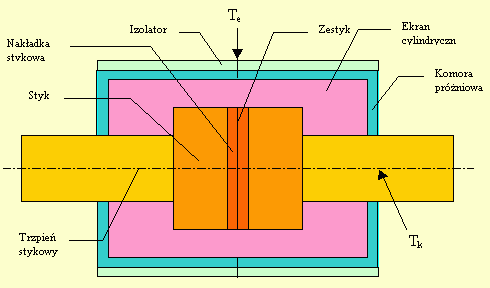


Równanie bilansu ciepła dla elementu dx toru pršdowego w stanie ustalonym i przy przepływie pršdu przemiennego ma postać:
dq - dq₁ - dq₂ + q₃ - q₄ = 0
przy czym:
dq - ciepło wytworzone przez przepływ pršdu;
dq₁ - ciepło przejmowane przez otoczenie z powierzchni elementu dx toru;
dq₂ - ciepło zużyte na nagrzanie elementu dx toru;
q₃ - ciepło przekazywane przez przewodzenie do elementu dx toru;
q₄ - ciepło odprowadzone przez przewodzenie z elementu dx toru.
Rozwišzanie równania bilansu dla stanu cieplnie ustalonego uzyskano przy następujšcych warunkach brzegowych:
- T_n(0)=T_z dla x=0, P/2=-λ_ns_n(dT_n/dx)_x=0;
- T_n(x_n)=T_s(x_n) dla x=x_n, (dT_n/dx)_x=xn=(dT_s/dx)_x=xn;
- T_s(x_s)=T_t(x_s) dla x=x_s, (dT_s/dx)_x=xs=(dT_t/dx)_x=xs;
- T_t(x_t)=T_k dla x=x_t.
gdzie:

P - moc cieplna wydzielona w zestyku;

T_z - temperatura zestyku;

T_n - temperatura w nakłdce stykowej;

T_s - temperatura w styku;

T_t - temperatura w trzpieniu stykowym;

x_n - gruboœć nakładki;

x_s - długoœć obejmujšca nakładkę i styk;

x_t - długoœć od zestyku do wyjœcia trzpienia z komory próżniowej;

Uzyskany z rozwišzania równania bilansu wzór na rozkład temperatury wzdłuż osi toru pršdowego ma postać:

przy czym f₁(x) jest funkcjš pomocniczš okreœlonš zależnoœciš:

a f₂(x) jest funkcjš pomocniczš okreœlonš zależnoœciš:

temperaturę ustalonš wyznacza się z wzoru:

natomiast współczynnik a jest opisany wzorem:

W przedstawionych wzorach zastosowano oznaczenia:

Φ - strumień cieplny;

ρ - rezystywnoœć materiału toru;

α_o- współczynnik temperaturowy rezystancji;

λ - przewodnoœć cieplna właœciwa dla n-nakładki, s-styku, t-trzpienia;

s - przekrój poprzeczny;

A - jednostkowa powierzchnia boczna (obwód);

k_r - współczynnik przejmowania ciepła przez promieniowanie;

k_w - współczynnik wypierania pršdu (naskórkowoœci);

T_o- temperatura otoczenia (tu: T_o=T_e);

j - gęstoœć pršdu.

Równanie okreœlajšce temperaturę T w funkcji odległoœci x opisuje rozkład tej temperatury w zakresie x_s<x<=x_t, przy czym x_t jest długoœciš toru od zestyku do wyjœcia trzpienia z komory. W miejscu tym jest mierzona temperatura T_k. Bardzo łatwo można to równanie dostosować do zakresów: x_n<x<=x_s oraz 0<x<=x_n. W przypadku, gdy w torze pršdowym nie ma nakładki należy podstawić x_n=0 i T_un=T_us. Jeœli rozważany jest tor o stałym przekroju, to x_n=x_s=0 i T_un=T_us=T_ut.
Temperaturę w zestyku T_z, okreœlonš dla warunków, przy których powierzchnia rzeczywista stycznoœci jest równa powierzchni pozornej; pozwala wyznaczyć równanie:

Przejmowanie ciepła przez otoczenie w próżni

Przewód nagrzewany pršdem i zanurzony w gazie o bardzo niskim ciœnieniu oddaje ciepło do otaczajšcych go elementów o niższej temperaturze. Przejmowana moc cieplna jest proporcjonalna do różnicy temperatur toru i (w przedstawionym modelu) osłony kondensacyjnej - ekranu.
Współczynnik przewodnoœci cieplnej w warunkach molekularnych k_M dla współosiowych cylindrów o œrednicach d i d_e > d, można wyznaczyć z zależnoœci:

gdzie:

α - współczynnik akomodacji;

p - ciœnienie;

Λ_o - przewodnoœć cieplna swobodnych czšstek gazu w temperaturze 273^oK,

dla powietrza Λ_o=1,23 W/(m²K Pa).

Obliczenia, nawet przy stosunkowo niskiej próżni (p=1x10^-2Pa), pokazujš, że wartoœć współczynnika k_M jest przynajmniej o rzšd mniejsza od wartoœci współczynnika przejmowania ciepła przez promieniowanie. Na tej podstawie w dalszej analizie pominięto moc cieplnš oddawanš drogš molekularnš.
Współczynnik przejmowania ciepła przez promieniowanie k_r można oszacować z zależnoœci:

przy czym:

σ_o - stała Stefana-Bolzmana;

ε - współczynnik emisyjnoœci toru pršdowego;

ε_e - współczynnik emisyjnoœci ekranu;

T_u - temperatura ustalona toru długiego.

Ostatni wzór można uproœcić gdy d<<d_e.
Korzystajšc z ostatniej zależnoœci i równania podanego wczeœnie na T_u, otrzymuje się zależnoœć pomiędzy T_u i T_e:

Zestyk - wewnętrzne Ÿródło ciepła

W wyniku przepływu pršdu na zestyku wydziela się ciepło, które powoduje dodatkowy wzrost temperatury. Jest on proporcjonalny do wartoœci rezystancji zestykowej. Na podstawie ustaleń R.Holm'a i P.Johannet'a dla styków czystych, górnš granicę spodziewanej wartoœci rezystancji zestykowej można obliczyć na podstawie zależnoœci teoretyczno-doœwiadczalnej:

gdzie:

H - twardoœć wg Brinell'a;

F - siła docisku styków;

ρ - rezystywnoœć.

Porównanie wyników obliczeń z wynikami pomiarów

W tabelce zestawiono wyniki obliczeń temperatury œrodka jednolitego toru pršdowego w próżni (p<1x10^-2Pa) z wynikami pomiarów.

Natężenie pršdu [A]	300	400	500	600
Temperatura obliczona [^oK]	344,3	364,7	393,2	417,7
Temperatura pomierzona [^oK]	343,9	367,1	397,4	427,8
Błšd względny [%]	0,12	0,65	1,10	2,40
Temperatura pomierzona Tk [^oK] przy xk=0,439 m	342,4	362,2	389,7	413,0

Tor pršdowy był wykonany z miedzi próżniowej. Œrednica toru była równa 20 mm.
Aby ułatwić obliczenia napisany został program o nazwie TEMP-TOR, który można œcišgnšć w formie spakowanej (29 kB). Program najlepiej uruchomić w systemie DOS lub w wersji pełnoekranowej w oknie systemu Windows.
Pstryknij tutaj nazwę programu: TEMP-TOR , aby go œcišgnšć i zapisać na własnym dysku.
Dla celów dydaktycznych program można używać bezpłatnie.

---