Sprawozdanie z ćwiczenia A-21

Jacek Kuś Artur Gmaj	Zespół nr 6.
Wydział Elektryczny	Ocena z przygotowania:
Piątek 1415 - 1700	Ocena ze sprawozdania:
Data : 20-05-94	Zaliczenie:
Prowadzący: dr Panecki	Podpis:

Temat: Modelowanie procesu powstawania błędów przypadkowych.

Cel ćwiczenia:

Celem ćwiczenia jest prześledzenie procesu powstawania błędów przypadkowych przy użyciu tablicy Galtona i przeprowadzenie analizy wyników pomiarów w zależności od kąta nachylenia tablicy oraz od ilości pomiarów. Celem doświadczenia jest także porównanie otrzymanego rozkładu wyników z rozkładem teoretycznym Gaussa. W ćwiczeniu należy także określić warunki w jakich tablicę Galtona można wykorzystywać do symulacji procesu powstawania błędów przypadkowych.

Wykonanie ćwiczenia:

Ćwiczenie przeprowadziliśmy przy pomocy tablicy Galtona. Zrealizowaliśmy szereg niezależnych serii pomiarowych składających się z różnej liczby elementów (kulek). Maksymalna ilość elementów była określona parametrami tablicy - wysokość kolumny. W dalszej kolejności powtórzyliśmy próby dla maksymalnej liczby kulek ustawiając tablicę pod trzema różnymi kątami.

Opracowanie wyników:

W ćwiczeniu otrzymaliśmy następujące wyniki:

Badanie zależności
,
od ilości pomiarów:

Lp.	n
1	592	1,189	5,445	0,224	37.3
2	192	0,271	6,716	0,485	56.7
3	91	0,321	6,375	0,683	65.8
4	48	0,558	6,324	0,913	-
5	19	0,263	6,054	1,389	-

gdzie:

n - ilość pomiarów

- wartość średnia otrzymanych wyników

- błąd standardowy pojedynczego pomiaru wyrażony wzorem: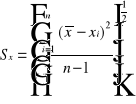

- odchylenie standardowe średniej wyrażone wzorem:

- wartość testu obliczona wzorem
zaś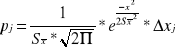

m - ilość przedziałów

Zbadaliśmy także wpływ kąta nachylenia tablicy Galtona na powyższe wielkości:

kąt
	1,189	5,445	0,224
	0,886	5,112	0,270
	0,852	5,063	0,205

>
>

W celu porównania rozkładu doświadczalnego z rozkładem teoretycznym wykonaliśmy następujące histogramy:

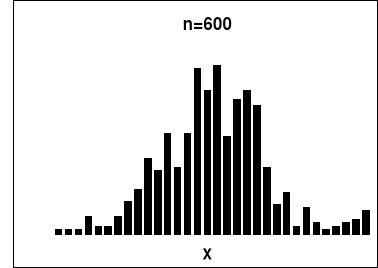
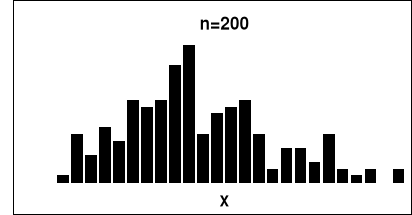
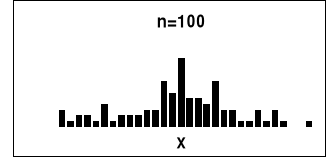
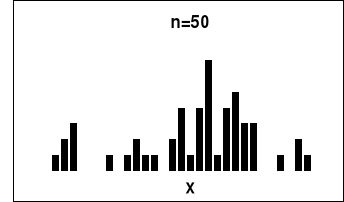
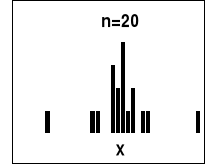
Wnioski:

1. W ćwiczeniu badaliśmy zmienność parametrów: odchylenia standardowego pojedynczego pomiaru (
) i odchylenia standardowego średniej (
) w zależności od ilości pomiarów. Stwierdziliśmy, że
maleje wraz ze wzrostem ilości pomiarów, natomiast
nie zależy od ilości pomiarów.

2.W ćwiczeniu badaliśmy także zgodność rozkładu wyników doświadczalnych z teoretycznym rozkładem Gaussa i doszliśmy do następujących wniosków:

- tylko przy dużej liczbie pomiarów rozkład doświadczalny można porównywać z rozkładem normalnym;

- rozkłady dla małej liczby pomiarów: 20, 50, 100 nie odzwierciedlają procesu symulacji procesu powstawania błędów przypadkowych, ich rozkład odbiega od rozkładu teoretycznego;

- powyższe wyniki potwierdza test
, który dla liczby pomiarów n=600 wynosi 37,3 (poziom ufności=0.22). Obliczone wartości dla pozostałych serii pomiarowych przekroczyły wartość krytyczną testu, w związku z tym wnioskujemy, że nie odzwierciedlają one rozkładu Gaussa.

3. Wyniki naszego doświadczenia wskazują także, iż kąt nachylenia tablicy nie ma wpływu na otrzymane rezultaty.

4. Powyższe doświadczenie dowodzi tezy: aby tablicy Galtona używać do symulacji procesu powstawania błędów przypadkowych należy badać dużą liczbę kulek.

Obliczenia parametrów charakteryzyjących rozkład Gaussa dokonaliśmy przy pomocy komputera. Listing użytego programu dołączmy do sprawozdania.

Sprawozdanie z ćwiczenia A-21 strona 4