Które z podanych algebr są grupami (symbole 
i ⋅ oznaczają tu zwykłe dodawanie i mnożenie liczb z danego zbioru):
Algebra wyższa, lista 2
Które z podanych algebr są grupami (symbole
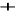
i ⋅ oznaczają tu zwykłe dodawanie i mnożenie liczb z danego zbioru):
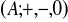
, gdzie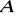 
jest jednym ze zbiorów: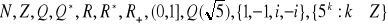
;
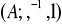
, gdzie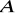 
jest jednym ze zbiorów: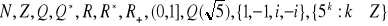 
?
Sprawdź, czy dany zbiór macierzy tworzy grupę względem mnożenia macierzy:
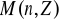
; b)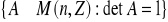 
; c)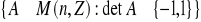 
; d)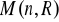 
;
e) 
; f) 
.
Sprawdź, czy zbiór funkcji 
(
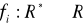
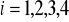
) tworzy grupę względem składania funkcji jeśli: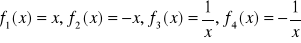 
.
Sprawdź, czy zbiór funkcji 
(
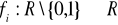
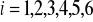
) tworzy grupę względem składania funkcji jeśli: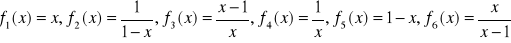 
.
Niech 
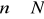
. Sprawdzić, że zbiór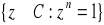 
pierwiastków zespolonych stopnia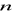 
z liczby 1 jest grupą względem mnożenia liczb.
Niech 
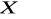
. Udowodnić, że zbiór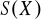 
wszystkich bijekcji zbioru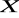 
na siebie jest grupą względem składania odwzorowań.
Zbadać, czy zbiór tych bijekcji 
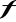
zbioru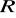 
na siebie, które spełniają podany warunek, tworzy grupę przekształceń zbioru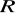 
(tzn. jest podgrupą grupy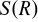 
):
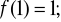
b)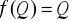 
, c)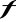 
jest funkcją rosnącą, d)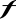 
jest funkcją ściśle monotoniczną,
e) 
jest funkcją nieparzystą, f) 
dla prawie wszystkich 
.
Wykazać, że w grupie 
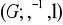
zachodzi równość: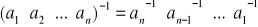 
dla dowolnych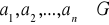 
.
Wykazać, że w grupie 
zachodzi równość: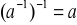 
dla dowolnego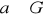 
.
Wykazać, że w grupie 
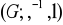
dla dowolnych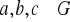 
prawdziwe są następujące prawa skracania: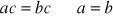 
oraz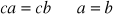 
.
Wykazać, że jeśli w grupie 
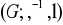
dla każdego 
zachodzi równość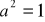 
, to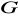 
jest grupą abelową.
Niech 
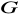
i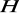 
będą grupami. Pokazać, że iloczyn kartezjański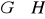 
też jest grupą.
Które z następujących podzbiorów zbioru 
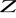
są podgrupami grupy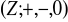 
:
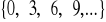
; b)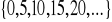 
, c)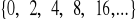 
,
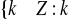
jest wielokrotnością 4}, e)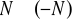 
? Przedstaw te podgrupy w postaci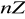 
.
Czy zbiór 
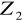
jest podgrupą grupy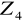 
?
Wyznaczyć wszystkie podgrupy grupy: a) 
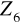
, b)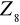 
?
Niech 
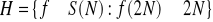
. Czy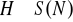 
?
Niech 
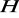
będzie zbiorem wszystkich ciągów arytmetycznych o wyrazach rzeczywistych. Czy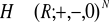 
?
Niech 
i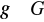 
. Pokaż, że zbiór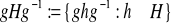 
jest podgrupą grupy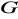 
.
Niech 
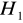
i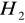 
będą podgrupami grupy abelowej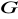 
. Niech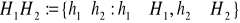 
. Pokaż, że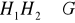 
oraz że podgrupa ta jest najmniejszą (w sensie inkluzji) podgrupą grupy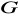 
zawierającą każdą z podgrup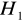 
i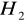 
.
Niech 
i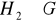 
. Udowodnić, że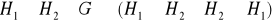 
.
Niech 
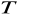
. Udowodnić, że jeśli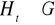 
dla każdego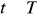 
, to również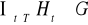 
.
Korzystając z poprzedniego zadania, wykazać, że jeżeli 
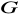
jest grupą oraz 
, to istnieje najmniejsza w sensie inkluzji podgrupa grupy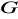 
zawierająca zbiór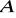 
. (Podgrupę tę nazywamy podgrupą generowaną przez zbiór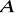 
i oznaczamy przez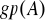 
; jeżeli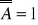 
, to podgrupa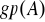 
zwie się cykliczną).
Niech 
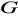
będzie grupą i niech 
. Wykazać, że
.
Jeśli 
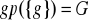
dla pewnego elementu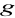 
grupy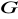 
, to element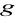 
nazywa się generatorem grupy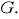 
Znajdź wszystkie generatory grupy: a)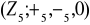 
, b)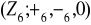 
.
Rzędem elementu 
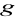
grupy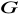 
nazywamy liczbę elementów grupy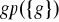 
i oznaczamy przez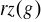 
. Można pokazać, że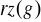 
jest równy najmniejszej dodatniej liczbie całkowitej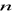 
dla której zachodzi: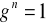 
(jeśli taka liczba nie istnieje to piszemy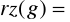 
). Wyznaczyć rząd elementu grupy: a)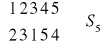 
, b)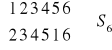 
, c)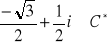 
, d)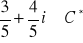 
.
Niech 
. Udowodnij, że relacja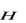 
określona w zbiorze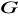 
wzorem: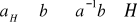 
(
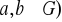
jest relacją równoważności i dla dowolnego elementu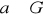 
klasą abstrakcji elementu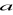 
jest warstwa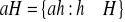 
.
Wyznaczyć warstwy grupy 
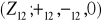
względem poniższej jej podgrupy: a) {0}; b) {0, 6}, c) {0, 4, 8}, d) {0, 3, 6, 9}, e) {0, 2, 4, 6, 8, 10}; f)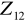 
.
Opisać warstwy grupy 
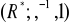
względem jej podgrupy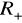 
.
Opisać warstwy grupy 
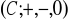
względem jej podgrupy R.
Wykaż, że dla każdego elementu 
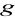
grupy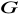 
warstwa prawostronna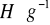 
składa się z odwrotności elementów warstwy lewostronnej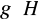 
.
Udowodnić, że jeśli 
, to zbiory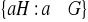 
i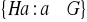 
są równoliczne. (wskazówka: rozważ funkcję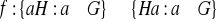 
określoną wzorem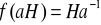 
)
Podaj przykład przekształcenia wzajemnie jednoznacznego podgrupy 
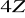
na jej warstwę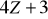 
w grupie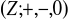 
.
Przedstaw grupę 
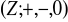
w postaci rozłącznej sumy pięciu warstw pewnej jej podgrupy.
Niech 
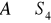
oraz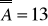 
. Pokaż, że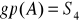 
. Czy grupa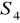 
jest cykliczna?
Niech 
oraz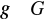 
. Pokaż, że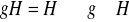 
.
Niech 
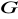
będzie grupą skończoną, 
oraz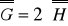 
. Wykaż, że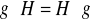 
dla każdego elementu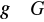 
(tzn. podgrupa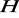 
jest podgrupą normalną grupy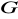 
).
Opisać elementy grupy ilorazowej 
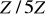
i zbudować tabelkę dodawania w tej grupie.
Niech 
, 
, 
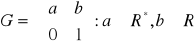
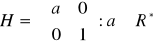
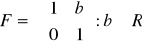
. Udowodnić, że: zbiór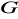 
z działaniem mnożenia macierzy tworzy grupę; 
, lecz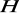 
nie jest podgrupą normalną grupy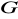 
oraz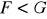
.
Niech 
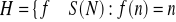
dla prawie wszystkich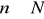 
}. Sprawdzić, że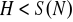 
.
Sprawdzić, że zbiór 
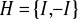
jest dzielnikiem normalnym grupy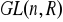 
(symbol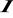 
oznacza tu macierz jednostkową w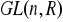 
).
Niech 
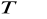
. Udowodnić, że jeśli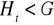 
dla każdego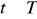 
, to również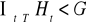 
.
Wykazać, że jeśli 
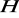
i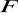 
są podgrupami normalnymi grupy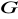 
, to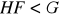 
, gdzie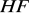 
jest podgrupą zdefiniowaną w zadaniu 18.
Sprawdź, że wzór 
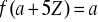
nie określa funkcji o dziedzinie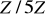 
i przeciwdziedzinie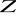 
.
Niech 
. Podać warunek konieczny i dostateczny na to, by wzór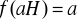 
określał funkcję, której dziedziną jest zbiór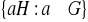 
, a przeciwdziedziną jest zbiór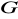 
.
Niech 
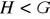
. Udowodnić, że grupa ilorazowa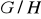 
jest abelowa wtedy i tylko wtedy, gdy spełniony jest warunek: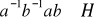 
dla dowolnych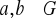 
.
Niech 
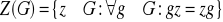
(zbiór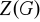 
nazywa się centrum grupy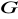 
). Sprawdź, że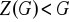 
oraz grupa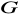 
jest abelowa wtedy i tylko wtedy, gdy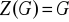 
.
Opisać centrum: a) iloczynu kartezjańskiego 
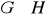
za pomocą centrum grupy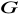 
i centrum grupy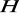 
; b) grupy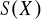 
; c) grupy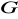 
z zadania 38.
Udowodnić, że dla każdej podgrupy normalnej 
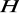
grupy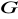 
relacja równoważności zdefiniowana w zadaniu 26 jest kongruencją grupy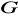 
.
Udowodnić, że dla dowolnej kongruencji ∼ grupy 
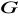
istnieje podgrupa normalna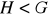 
taka, że dla dowolnych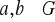 
zachodzi związek: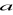 
∼
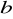
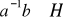
. (wskazówka: rozpatrzyć klasę abstrakcji elementu neutralnego grupy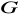 
)
Wskaż nieskończenie wiele grup 
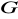
takich, że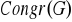 
składa się z dwóch elementów.
Które z następujących funkcji 
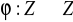
są homomorfizmami grupy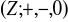 
w siebie?
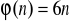
; b)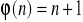 
; c)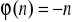 
; d)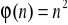 
; e)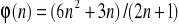 
.
Które z następujących funkcji 
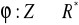
są homomorfizmami grupy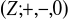 
w grupę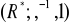 
? a)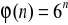 
; b)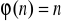 
; c)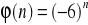 
; d)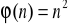 
; e)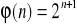 
.
Które z homomorfizmów z zadań 51 i 52 są izomorfizmami?
Wykaż, że funkcja 
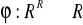
zadana wzorem: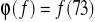 
jest homomorfizmem grupy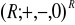 
w grupę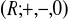 
.
Znajdź jądro każdego z następujących homomorfizmów 
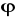
: a)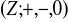 
w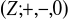 
dany wzorem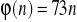 
; b)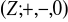 
w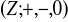 
dany wzorem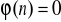 
dla wszystkich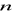 
;
c) 
w 
dany wzorem 
; d) 
w 
dany wzorem 
.
Dla każdego z homomorfizmów z zadania 55 znajdź tę warstwę jego jądra, do której należy liczba 73.
Niech 
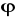
będzie pewnym homomorfizmem określonym na grupie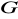 
, 
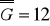
oraz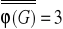 
.
znajdź 
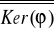
; b) ile elementów grupy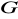 
homomorfizm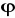 
przeprowadza na każdy z elementów grupy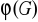 
?; c) ile wynosi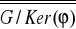 
?
Niech 
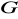
i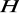 
będą grupami. Sprawdź, że przekształcenie: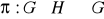 
zdefiniowane wzorem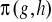 
=
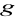
jest homomorfizmem. Znajdź jądro tego homomorfizmu. Znajdź dzielnik normalny grupy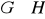 
, który jest izomorficzny z grupą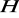 
.
Udowodnij, że jeżeli w grupie 
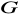
istnieje element o rzędzie równym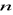 
, natomiast w grupie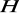 
nie ma elementu o rzędzie równym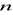 
, to grupy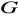 
i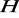 
nie są izomorficzne.
Zdefiniujmy funkcję 
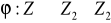
grupy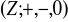 
w grupę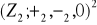 
wzorem: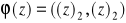 
. Sprawdź, że: a)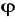 
jest homomorfizmem grupy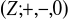 
w grupę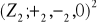 
; b)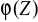 
jest podgrupą grupy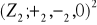 
; c) znajdź jądro tego homomorfizmu; d) czy grupa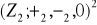 
jest izomorficzna z grupą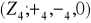 
?
Niech 
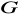
będzie grupą z zadania 38. Pokaż, że przekształcenie grupy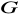 
w grupę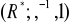 
zdefiniowane wzorem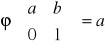 
jest homomorfizmem. Znajdź jądro tego homomorfizmu. Wykaż, że grupa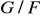 
, gdzie podgrupa normalna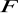 
jest określona w zad. 38, jest izomorficzna z grupą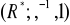 
.
Znajdź 
.
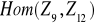
Udowodnij, że następujące pary grup nie są izomorficzne: a) 
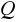
i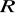 
; b)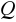 
i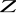 
; c)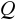 
i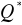 
;
d) 
i 
; e) 
i 
Udowodnić, że funkcja: a) 
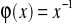
; b)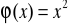 
jest elementem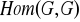 
wtedy i tylko wtedy, gdy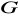 
jest abelowa.