WYZNACZANIE WSPÓŁCZYNNIKA ZAŁAMANIA ŚWIATŁA W SZKLE METODĄ KĄTA NAJMNIEJSZEGO ODCHYLENIA

1. Wstęp teoretyczny.

Pryzmatem optycznym nazywamy ośrodek załamujący światło, ograniczony nierównoległymi płaszczyznami. Linia przecięcia obu płaszczyzn nosi nazwę krawędzi łamiącej, a kąt zawarty między płaszczyznami - kąta łamiącego pryzmatu. Przekrój pryzmatu prostopadły do krawędzi łamiącej nazywamy przekrojem głównym. Pryzmaty ze szkła lub substancji stałej szlifowane są w postaci graniastosłupów trójkątnych, o przekroju głównym w postaci trójkąta. W przeprowadzonych tu rozważaniach będziemy rozpatrywali wiązki światła, które biegną w płaszczyznach głównych.

Jeżeli smukła wiązka światła białego pada na pryzmat pod kątem α, to ulega ona rozszczepieniu na barwną smugę, zwaną widmem, którą cechują różne kąty załamania dla różnych barw światła (rys.1).

Ponieważ kąt padania α dla wszystkich barw zawartych w świetle białym jest tu ten sam, a kąty załamania β są różne, wobec tego współczynnik załamania n = dla różnych barw jest różny. Dla każdej substancji współczynniki załamania różnych barw mają określone wartości.

Promień światła jednobarwnego padający na pryzmat pod kątem α₁ ulega dwukrotnie załamaniu i wychodzi z niego, doznając odchylenia, którego miarą jest kąt δ (rys.2). Z konstrukcji geometrycznej przedstawiającej bieg promieni wynika, że

δ = α_­1 - β₁ + α₂ - β_2,

lub inaczej,

δ = α₁ + α₂ - (β₁ + β₂);

ale

β₁ + β₂ = ϕ;

więc

δ = α₁ + α₂ - ϕ.

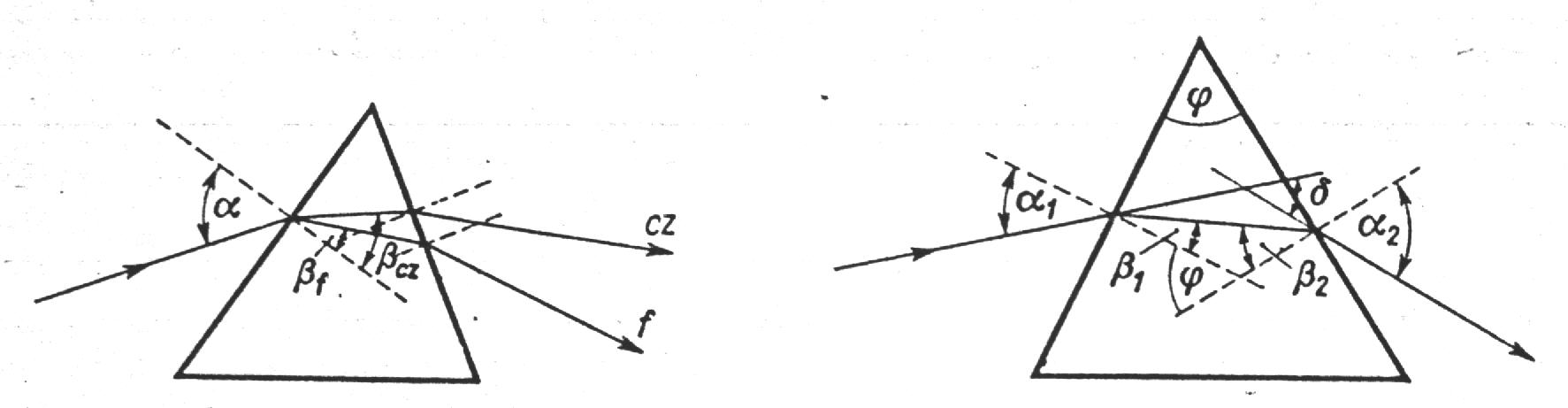
rys.1 Rozszczepienie światła białego. rys.2 odchylenie promienia jednobarwnego.

Kąt odchylenia δ zależy od kąta padania α₁, od współczynnika załamania pryzmatu n (α₂ zależy od n) i od kąta łamiącego ϕ. Kąt odchylenia osiąga minimum, gdy bieg promieni jest symetryczny w stosunku do pryzmatu, tzn. gdy wewnątrz pryzmatu promień jest prostopadły do dwusiecznej kąta łamiącego. Wówczas α₁ = α₂ = α oraz β₁ = β₂ = β, a równanie δ = α₁ + α₂ - ϕ przyjmuje prostszą postać

δ_min = 2α - ϕ.

Z równania tego wyznaczamy kąt α :

α = .

Na podstawie równania β₁ + β₂ = ϕ otrzymujemy :

β = .

Podstawiając znalezione wartości α i β do wzoru definiującego współczynnik załamania :

n =

otrzymujemy na n wzór następujący :

n = .

Mierząc kąt łamiący pryzmatu ϕ oraz kąt minimum odchylenia δ_min możemy wyznaczyć współczynnik załamania substancji, z której wykonany jest pryzmat.

Prawa wykorzystywane w ćwiczeniu:

• Prawo odbicia światła

Od powierzchni ciał światło odbija się zawsze w takim kierunku, że kąt odbicia jest równy kątowi padania i leżą one w jednej płaszczyźnie

• Prawo załamania światła

Na granicy dwóch ośrodków zachodzi załamanie światła tak, że stosunek kąta padania α do sinusa kąta załamania β dla dwóch ośrodków jest stały i nazywany jest współczynnikiem załamania światła n. Promień padający, załamany i normalna leżą w jednej płaszczyźnie.

n = sin α / sin β = v₁ / v₂ (prawo Snelliusa)

gdzie v₁ / v₂ oznacza stosunek prędkości światła padającego do prędkości światła załamanego.

• Zasada odwracalności biegu promienia

Gdy promień świetlny biegnie z ośrodka optycznie rzadszego do optycznie gęstszego, np. z powietrza do wody, wówczas ulega on załamaniu, zbliżając się w ośrodku gęstszym ku normalnej. W przypadku biegu odwrotnego promień załamany oddala się od normalnej.

• Zasada Fermata

Światło między dwoma dowolnymi punktami biegnie po takiej drodze, aby czas potrzebny na jej przebycie był jak najkrótszy. Oznacza to, że światło w ciałach przezroczystych i w próżni rozchodzi się po liniach prostych.

Etapy ćwiczenia:

1. Ustawienie spektrometru (wyzerowanie lunety).

2. Wyznaczenie kąta łamiącego pryzmatu.

3. Wyznaczenie kąta minimum odchylenia.

2. Wzory, wykresy, obliczenia.

I. Wyznaczanie kąta łamiącego pryzmatu :

Nr. Pomiaru	Odczyt z prawej	Odczyt z lewej
		ϕ1	ϕ2
1	306°11'8''	66°11'8''
2	318°8'52''	78°6'42''
3	309°16'34''	92°13'16''
4	312°20'16''	111°17'24''

Kąt łamiący pryzmatu dla wszystkich pomiarów wyznaczam ze wzoru:

• =

Z rozważań opartych na równaniu krzywej Gaussa okazuje się, iż jeśli ma się wiele pomiarów jakiejś wielkości, to najbardziej prawdopodobną wartością, a więc najbardziej zbliżoną do prawdziwej wartości jest średnia arytmetyczna wszystkich pomiarów. Jest to postulat średniej arytmetycznej. Tą metodą wyznaczę średnią wartość kąta łamiącego.

Nr. Pomiaru	ϕ	εi	εi^2
1	59°59'44''	2''	4''
2	59°59'47''	5''	25''
3	59°59'42''	0''	0''
4	59°59'33''	- 9''	81''
	ϕśr = 59°59'42''

ϕ - kąt łamiący pryzmatu

ϕ_śr - średnia wartość kąta łamiącego

Błąd średni kwadratowy wyznaczam ze wzoru:

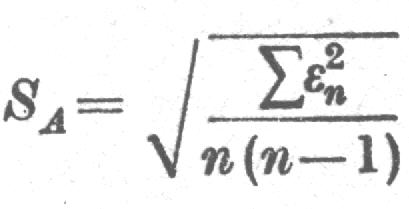
Średnia wartość kąta łamiącego pryzmatu uwzględniając dokładność przyrządu wynosi:

ϕ_śr = 59°59'42'' ± 0°00'04''

II. Wyznaczanie kąta najmniejszego odchylenia :

Barwa	Odczyt z prawej	Odczyt z lewej	Kąt minimum odchylenia
-	δ1	δ2	δmin
Czerwona	321°15'28''	38°33'24''	38°23'39''
Żółta	321°15'28''	38°48'28''	38°33'20''
Zielona	321°7'48''	38°48'28''	38°41'05''
Nieb. - ziel.	320°49'24''	39°6'38''	38°58'13''
Niebieska	320°23'44''	39°49'2''	39°20'13''

δ_min =

III. Obliczanie współczynnika załamania :

Barwa	ϕ śr	δmin	n
Czerwony	59°59'42''	38°23'39''	1,51398
Żółty			38°33'20''	1,51582
Zielony			38°41'05''	1,51729
Niebiesko - zielony			38°58'13''	1,52053
Niebieski			39°20'13''	1,52469

ϕ _śr - średnia wartość kąta łamiącego

δ_min - wartość kątów najmniejszego odchylenia dla poszczególnych barw

n - współczynnik załamania

n =

Błąd wyznaczę z różniczki zupełnej:

Δn = | n | * | Δϕ | + | n | * | Δδ |

Ponieważ wzór n = można zapisać również jako n =

i wtedy:

| n | =

| Δϕ | = 4'' / 3600'' = 1,1(1) * 10^-3 (błąd średni kwadratowy)

| n | =

| Δδ | = 2'' / 3600'' = 0,5(5) * 10^-3 (błąd przyrządu)

Barwa	N	Δn
Czerwony	1,51398	1,0939 *10^-3
Żółty	1,51582	1,0972 *10^-3
Zielony	1,51729	1,0992 *10^-3
Niebiesko - zielony	1,52053	1,1034 *10^-3
Niebieski	1,52469	1,1081 *10^-3

Dyspersja światła - zależność współczynnika załamania ośrodka (szkła) od długości fali świetlnej.

n - współczynnik załamania

λ - długość fali

3. Wnioski:

Pierwsza część ćwiczenia polegała na wyznaczeniu kąta łamiącego pryzmatu. Z uzyskanych wyników obliczyłam średnią wartość tego kąta ϕ_śr = 59°59'42''. Podczas doświadczenia wyniki pośrednie zostały wyznaczone 5 razy ale do obliczeń skorzystałem tylko z czterech z nich ponieważ jeden z wyników można zaliczyć do tzw. błędów grubych (prawdopodobnie złe odczytanie z przyrządu pomiarowego) i wprowadzałby duże, niepotrzebne błędy. Obliczyłem również błąd średni kwadratowy, który wynosi S_A = 0°00'03'', ale ponieważ dokładność przyrządu to 0°00'02'', więc przyjąłem S_A = 0°00'04''i wtedy ϕ_śr = 59°59'42'' ± 0°00'04''.

Następnie obliczyłem kąt minimum odchylenia δ_min dla kolejnych barw widma. Te dwie wielkości ϕ_śr i δ_min pozwoliły mi na obliczenie współczynnika załamania n. Dla różnych barw widma wynosi on od n = 1,514 do 1,528. Otrzymane przeze mnie wyniki były bardzo zbliżone do danych tablicowych (dla szkła cienkiego n = 1,515).

Również współczynnik załamania n obarczony był błędem. Do jego wyliczenia posłużyła metoda różniczki zupełnej. Błędy Δn były bardzo niewielkie (pierwsza jedynka na 3 miejscu po przecinku). Mając współczynnik załamania n i długość fali λ (odczytana z tablic) wyznaczyłem graficznie zależność n = f (λ).

Z przebiegu krzywej dyspersji można zauważyć, że wraz ze wzrostem fali maleje współczynnik załamania. Jest to jednak zależność nieliniowa i niemonotoniczna.

---