2008-12-05
Sprawozdanie
Temat : Badanie interferencji światła: pierścienie Newtona i prążki w klinie powietrznym.
1. Opis ćwiczenia.
Na soczewkę płasko-wypukłą, leżącą na płaskiej płytce szklanej, pada wiązka monochromatycznego światła o długości λ, skierowana prostopadle do powierzchni płytki. Promienie odbite od wypukłej strony soczewki będą interferowały z promieniami odbitymi od górnej powierzchni płytki, gdyż są wzajemnie spójne jako pochodzące z podziału tego samego promienia macierzystego, a różnica dróg optycznych pomiędzy nimi nie jest duża.
W zależności od różnicy faz nakładających się promieni wystąpi wzmocnienie lub osłabienie natężenia światła. Ponieważ punkty o tej samej różnicy faz będą leżały na okręgach, zaobserwujemy w mikroskopie rodzinę na przemian ciemnych i jasnych współśrodkowych pierścieni. (ciemne pierścienie to pierścienie Newtona)
Poniższy rysunek przedstawia bieg promieni przy powstawaniu pierścieni Newtona, oraz obraz pierścieni Newtona w mikroskopie
Tak więc promień krzywizny obliczamy ze wzoru :
,
gdzie rm- promień pierścienia Newtona
λ- długość fali padającej
m -rząd interferencji
W drugiej części ćwiczenia należało przy znanym promieniu krzywizny soczewki obliczyć długość światła padającego na układ.
gdzie rm- promień pierścienia Newtona
λ- długość fali padającej
m -rząd interferencji
R - promień krzywizny
2. Wyniki pomiarów i obliczenia:
Poniższa tabelka przedstawia wyniki pomiarów pierwszej części ćwiczenia tj. pomiaru promienia krzywizny soczewki przy znanej długości fali padającej.
x1 i x2 są wartościami odczytanymi ze skali stolika dla przeciwległych krańców prążka; różnica tych wartości da nam średnicę prążka, a podzielona przez 2 da nam promień
m - nr prążka
Lp. |
m |
x1 [mm] |
x2[mm] |
d [mm] |
rm[mm] |
1 |
1 |
13,76 |
12,22 |
1,54 |
0,77 |
2 |
2 |
14,13 |
11,85 |
2,28 |
1,14 |
3 |
3 |
14,36 |
11,58 |
2,78 |
1,39 |
4 |
4 |
14,59 |
11,37 |
3,22 |
1,61 |
5 |
5 |
14,82 |
11,21 |
3,61 |
1,805 |
6 |
6 |
14,95 |
11,05 |
3,9 |
1,95 |
7 |
7 |
15,03 |
10,9 |
4,13 |
2,065 |
8 |
8 |
15,29 |
10,73 |
4,56 |
2,28 |
9 |
9 |
15,41 |
10,56 |
4,85 |
2,425 |
10 |
10 |
15,58 |
10,45 |
5,13 |
2,565 |
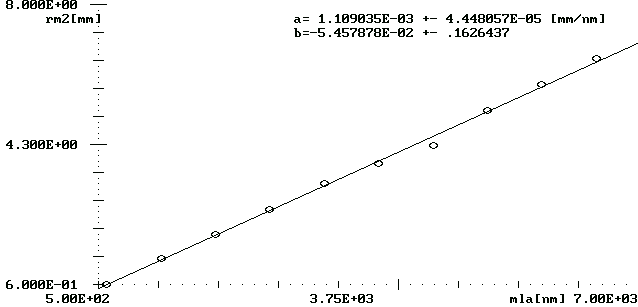
Wartość R- promienia krzywizny obliczamy metodą sumy najmniejszych kwadratów, podstawiając y=rm2 i x=λm, tak więc R=a. λ=589,3 [nm].
R=1,109035*10-3[mm2/nm]=1109,035[mm]
Błąd tak obliczonej wartości promienia krzywizny jest równy :
ΔR=±4,448057*10-5[mm2/nm]= ±44,48057[mm]
Tak więc :
R=1109±44[mm]
Obliczanie wartości λ- długości światła padającego przy znanym promieniu krzywizny:
Poniższa tabelka przedstawia wyniki pomiarów i obliczenia:
x1 i x2 są wartościami odczytanymi ze skali stolika dla przeciwległych krańców prążka; różnica tych wartości da nam średnicę prążka, a podzielona przez 2 da nam promień
m - nr prążka
Lp |
m |
x1[mm] |
x2[mm] |
d [mm] |
rm[mm] |
1 |
1 |
12,2 |
13,75 |
1,55 |
0,775 |
2 |
2 |
11,84 |
14,11 |
2,27 |
1,135 |
3 |
3 |
11,53 |
14,4 |
2,87 |
1,435 |
4 |
4 |
11,34 |
14,67 |
3,33 |
1,665 |
5 |
5 |
11,15 |
14,8 |
3,65 |
1,825 |
6 |
6 |
10,98 |
14,95 |
3,97 |
1,985 |
7 |
7 |
10,82 |
15,15 |
4,33 |
2,165 |
8 |
8 |
10,65 |
15,29 |
4,64 |
2,32 |
9 |
9 |
10,54 |
15,43 |
4,89 |
2,445 |
10 |
10 |
10,38 |
15,59 |
5,21 |
2,605 |
Wartość λ obliczamy metodą sumy najmniejszych kwadratów, podstawiając y=rm2 i x=Rm, tak więc λ=a. R=1109 [mm].
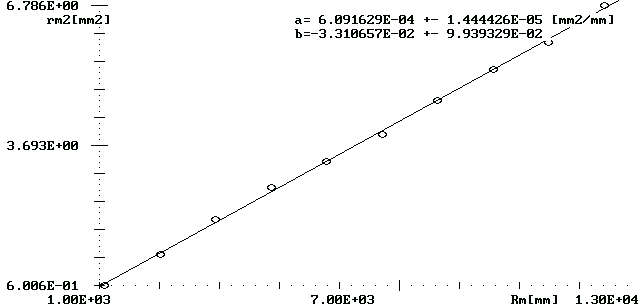
λ=6,091629*10-4[mm]= 609,1629 [nm]
Błąd tak obliczonej wartości promienia krzywizny jest równy :
Δλ=±1,444426*10-5[mm]= ±14,44426 [nm]
Tak więc :
λ=609 ±14 [nm]
W trzeciej części ćwiczenia dokonywaliśmy pomiaru współczynnika załamania światła przy pomocy zjawiska powstawania prążków Newtona. Ciałem o nieznanym współczynniku załamania światła była woda, która została wprowadzona pomiędzy soczewkę, a płytkę płasko równoległą.
Współczynnik załamania światła obliczamy ze wzoru:
![]()
Wyniki pomiarów i obliczenia:
Lp. |
m |
x1 [mm] |
x2 [mm] |
d [mm] |
r [mm] |
n [mm] |
Δx1 [mm] |
Δx2 [mm] |
Δr1 [mm] |
Δr2 [mm] |
Δn1 |
Δn2 |
Δn |
1 |
1 |
15,25 |
13,39 |
1,86 |
0,93 |
0,755617644 |
14,23 |
14,36 |
0,36 |
0,49 |
5,042698 |
2,721923 |
2,320775353698 |
2 |
2 |
15,53 |
13,2 |
2,33 |
1,165 |
0,963044005 |
14,47 |
14,56 |
0,6 |
0,69 |
3,630743 |
2,745363 |
0,885379618778 |
3 |
3 |
15,72 |
13 |
2,72 |
1,36 |
1,060013571 |
14,65 |
14,73 |
0,78 |
0,86 |
3,222553 |
2,650894 |
0,571658899794 |
4 |
4 |
15,81 |
12,83 |
2,98 |
1,49 |
1,177485158 |
14,81 |
14,84 |
0,94 |
0,97 |
2,958505 |
2,778334 |
0,180170392564 |
5 |
5 |
15,89 |
12,67 |
3,22 |
1,61 |
1,26062594 |
14,87 |
14,91 |
1 |
1,04 |
3,267669 |
3,021143 |
0,246525286243 |
6 |
6 |
15,96 |
12,62 |
3,34 |
1,67 |
1,406003155 |
14,93 |
14,99 |
1,06 |
1,12 |
3,489856 |
3,125958 |
0,363897612096 |
7 |
7 |
16,04 |
12,53 |
3,51 |
1,755 |
1,485291808 |
15,04 |
15,1 |
1,17 |
1,23 |
3,341907 |
3,023819 |
0,318087478150 |
8 |
8 |
16,09 |
12,44 |
3,65 |
1,825 |
1,569756307 |
15,15 |
15,21 |
1,28 |
1,34 |
3,191083 |
2,911712 |
0,279370779723 |
Wartość średnią n oraz błąd tej wartości obliczamy przez średnią ważoną, gdyż każdy z wyników pomiarów obarczony był innym błędem.
nśr=1,259624518
Δnśr= 0,496645976883
nśr=1,3±0,5
Wnioski:
Wyniki pierwszej części ćwiczenia były stosunkowo dokładne. Błędy pomiarowe wynikały głównie z niedokładnego wykonania soczewki. Promień krzywizny obliczony tą metodą jest dokładny lecz błąd tego pomiaru nie odzwierciedla niedokładności soczewki. Pomiar długości fali świetlnej tą metodą jest także dokładny lecz często nie jest możliwe dokonanie pomiarów większej liczby prążków, przez co dokładność się zmniejsza.
Wyniki trzeciej części pomiaru są mało dokładne gdyż woda pod soczewką uniemożliwia dokładne przyleganie wierzchołka soczewki do płytki płasko-równoległej, a co za tym idzie prążek rzędu zerowego nie jest idealnie „wygaszony”.
![]()
Wyszukiwarka
Podobne podstrony:
Laborka-25, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI - sprawozdan
spr-122, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI - sprawozdania,
WYDZIA~1, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI - sprawozdania
Fizyka cw 123 wyniki, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI -
półprzewodnikowe złącze p-n, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LAB
Lab 8 - Polarymetr, sprawozdanie Magdy 74, GRUPA 10
Lab 4 - Elektroliza, Sprawozdanie 4 (Elektroliza), Wydział
TiSP - dok, Lab TiSP - Sprawozdanie, PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA
TiSP - dok, Lab TiSP - Sprawozdanie, PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA
lab 01 sprawozdanie
LAB113, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI - sprawozdania,
laborka37, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI - sprawozdani
41konspekt, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI - sprawozdan
Wyniki do ćwiczenia 82 dla dave, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!
LAB 0 P, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI - sprawozdania,
lab73moja, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI - sprawozdani
więcej podobnych podstron