TEMAT: WYZNACZANIE MODUŁU SZTYWNOŚCI METODĄ DYNAMICZNĄ :

Celem ćwiczenia jest wyznaczenie występującego w prawie Hook ' a modułu sztywności przez pomiar okresu sprężystych drgań obrotowych .

Ciało nazywamy sprężystym , jeżeli odkształcenia , wywołane działającymi na nie siłami ,znikają zupełnie po usunięciu tych sił . Każde ciało zbudowane jest z atomów lub cząsteczek , między którymi działają siły nazywane siłami międzycząsteczkowymi . W ciałach stałych siły te są na tyle duże , że cząsteczki są uporządkowane i tworzą regularną strukturę przestrzenną ,nazywaną

siecią krystaliczną . Każda cząsteczka nazwana węzłem sieciowym ma swoje położenie równowagi , wokół , którego wykonuje niewielkie ,chaotyczne drgania . Powstanie stanu równowagi trwałej , wynika z faktu , że między kolejnymi dwiema cząsteczkami występują dwojakiego rodzaju siły :przyciągania oraz odpychania . Siły odpychania rosną zawsze znacznie bardziej wraz ze zbliżaniem się cząsteczek niż sily przyciągania .

Siła przyciągania opisana jest wzorem :

Siła odpychania opisana jest wzorem :
,

stałe a i b zależą od budowy znajdującej się w wężle sieci cząsteczki oraz rodzaju sił wiązania .

Każda cząsteczka w krysztale ma określoną energię potencjalną oraz kinetyczną .

Rozróżniamy cztery rodzaje wiązań atomów lub cząsteczek w ciałach stałych :

1.Jonowe (heteropolarne lub walencyjne) - które powstaje na skutek przyciągania się na przemian rozmieszczonych różnoimiennych jonów np . w kryształach NaCl , KCl .

2.Atomowe (homepolarne lub kowalencyjne) - które jest wynikiem tego , że pewne sąsiadujące ze sobą atomy zawierają wspólne dwa elektrony np . diament , grafit , krzem , german .

3.Metaliczne , które wynika z tego ,że istnieje grupa elektronów wspólna wszystkim atomom kryształu . Nazywamy je grupą lub "chmurą" elektronów swobodnych .

4.Van der Waalsa (cząsteczkowe) - w kryształach o tym typie wiązania w węzłach sieci znajdują się obojętne cząsteczki .Siły oddziaływania między nimi powstają na skutek oddziaływania ich wewnętrznych pól elektrycznych oraz oddziaływania drgających ładunków elektrycznych .

Siły działające na ciało wywołują ich odkształcenia . Wszelkie odkształcenia można sprowadzić do trzech głównych rodzajów odkształceń :

1.Odkształcenie jednostronne występuje wtedy , gdy siły działają na dwie przeciwległe ścianki ciała prostopadle do nich .

2.Odkształcenie wszechstronne występuje wtedy ,gdy na każdy element powierzchni ciała działa siła do niego prostopadła .

3.Ścinanie następuje wtedy , gdy działające siły są styczne do powierzchni ciała .

Naprężeniem nazywamy wektor o wartości równej stosunkowi wartości siły do powierzchni , na którą ona działa , o kierunku i zwrocie zgodnym z kierunkiem siły :

Jednostką naprężenia jest takie naprężenie , jakie wywołuje jednostkowa siła działając na jednostkową powierzchnię .W układzie SI jednostką naprężenia jest paskal (P) :jest to naprężenie jakie wywołuje siła jednego niutona działając na powierzchnię jednego metra kwadratowego .

Prawo Hooke'a formułuje zależność między naprężeniem a odkształceniem :

Jeżęli naprężenia w ciele są dostatecznie małe , to wywołane przez nie odkształcenie względne są do nich wprost proporcjonalne .

;
;
.

Współczynniki proporcjonalności 1/E , 1/K , 1/G nazywamy współczynnikami sprężystości , a ich odwrotności modułami :

E - moduł Younga ; K - moduł ściśliwości ; G - moduł sztywności . Są to stałe materiałowe.

Pośród metali największe wartości modułu sztywności ma stal G = 79500 MPa , a najmniejsze

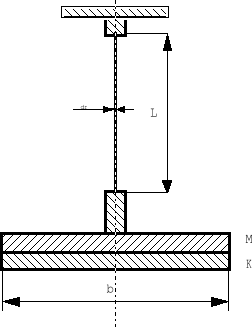
aluminium G = 26500 MPa . Stałą materiałową zwaną modułem sztywności G możemy wyznaczyć poprzez pomiar okresu sprężystych drgań obrotowych układu przedstawionego na rysunku 1 .

WZÓR KOŃCOWY:

a / forma podręcznikowa

l = długość pręta

m = masa dodatkowej tarczy K

r = promień pręta

R = promień dodatkowej tarczy K

T = okres drgań układu bez dodatkowej tarczy

T1 = okres drgań układu z dodatkową tarczą K

b / forma zawierająca bezpośrednie wielkości mierzone

.

b = średnica tarczy K mierzona suwmiarką o dokładności 0,05mm

d = średnica pręta mierzona śrubą mikrometryczną o dokładności 0,01mm

m = masa dodatkowej tarczy K mierzona wagą elektoniczną o dokładności 0,1 g

n = liczba drgań wahadła

t = czas , w którym wahadło układu bez dodatkowej tarczy wykonało n drgań

t1 = czas ,w którym wahadło układu wykonało n drgań z dodatkową tarczą

l = długość pręta

W doświadczeniu liczba drgań n wynosi 20 . Dla n = 20 wzór ma postać :

Rysunek 1 : Schemat wahadła torsyjnego :

M - tarcza stała

K - tarcza wymienna

2.Obliczenia pomiarów doświadczenia oraz błędy :

lp.	l[mm]	b[mm]	m[g]	t[s]	tn[s]	d[mm]	n
1.	631	139,7	376,1	53,081	93,952	0,59	20
2.	631	139,7	376,1	53,032	93,957	0,59	20
3.	631	139,7	376,1	52,796	95,369	0,59	20
4.	631	139,7	376,1	62,731	81,914	0,59	20
5.W.śr.	631	139,7	376,1	52,969	94,426	0,59	20
6.	631	140,8	376,1	51,366	62,019	0,58	20
7.	631	140,8	376,1	51,366	62,065	0,58	20
8.	631	140,8	376,1	59,225	62,775	0,58	20
9.	631	140,8	376,1	78,381	63,420	0,58	20
10.W.śr	631	140,8	376,1	53,986	62,286	0,58	20
11.	631	139,9	376,1	52,503	62,744	0,57	20
12.	631	139,9	376,1	52,242	62,516	0,57	20
13.	631	139,9	376,1	59,567	62,637	0,57	20
14.	631	139,9	376,1	77,147	73,987	0,57	20
15.W.śr	631	139,9	376,1	54,771	62,632	0,57	20
wartość średnia	631	140,1	376,1	53,909	73,114	0,58	20
błąd pomiar	0,5	0,05	0,1	0,001	0,002	0,008	0

Przykładowe obliczenia:

G ś = 6400*19628,01*631*376,1*3,14/0,113(5345,657-2906,181) = 3,395812*

G 1 = 6400*19516,09*631*376,1*3,14/0,121(8916,269-2805,715) = 1,257033*

G 2 = 6400*19824,64*631*376,1*3,14/0,113(3879,546-2914,488) = 8,657299*

G 3 = 6400*19572,01*631*376,1*3,14/0,106(3922,767-2999,862) = 9,5812321*

Do obliczenia błędu , z jakim wyznaczono moduł sztywności G , można - mimo iż w mianowniku występuje różnica - posłużyć się metodą różniczki logarytmicznej :

.Zakładamy , że

oraz

.

Błąd względny wyraża się wzorem :

Dm/m = 0,1/376,1 = 0,000265887

2Db/b = 0,1/140,1 = 0,000713776

Dl/l = 1/631 = 0,001584786

4Dd/d = 0,032/0,58 = 0,055172414

2Dt/t1 -t = 0,002/19,205 = 0,00010414

Błąd względny DG/G wynosi 0,0578407 = 5,78 % E = DG/G = 5,78 %

Błąd bezwzględny DG = E*G = 0,19641614*

3.Dyskusja błędów i wnioski z doświadczenia :

W doświadczeniu wykorzystaliśmy następujące urządzenia : suwmiarka , śruba mikrometryczna ,

waga elektroniczna oraz elektroniczny licznik mierzący czas.Błąd pomiarów został spowodowany niedokładnością przyrządów pomiarowych , nieprecyzyjnym odczytem wyników podczas przeprowadzania doswiadczenia .Skorzystaliśmy z podanych przyrządowych błędów ;

śruba mikrometryczna z podziałką o dokładności 0,01 mm , a suwmiarka z noniuszem o dokładności 0,05 mm .Do obliczenia błędu z jakim wyznaczono moduł sztywności G posłużyliśmy się metodą różniczki logarytmicznej , a do obliczenia błędu średnicy drutu wykorzystaliśmy wartość średniego błędu bezwzględnego pomiarów . Nasze ćwiczenie składało się z 3 serii pomiarów po 4 pomiary każdy , z tym że jeden pomiar pominęliśmy ze względu na zbyt duże różnice w porównaniu z innymi pomiarami i pomiaru tego nie uwzględnialiśmy do obliczania wartości średnich . Liczba drgań wahadła n = 20 i wykonując ten pomiar musieliśmy mierzyć pośrednie czasy , które mogą być niezbyt dokładne z powodu włączania i wyłączania elektronicznego licznika . Na wyliczony błąd tej wielkości / moduł sztywności / wpływają błędy poszczególnych wielkości mierzonych w doświadczeniu .

---