Wydział: MECH. DIAGNOSTYKA I REMONTY MASZYN I URZĄDZEŃ OKRĘTOWYCH |
PRACOWNIA FIZYCZNA
|
Rok szkolny: 98/99 |
Nr ćwiczenia: 5
|
Temat: Wyznaczanie momentu bezwładności żyroskopu |
Data oddania : 18.12. 98r.
|
Wykonał : A. Jasłowski IME a
|
Sprawdził: |
Ocena: |
TEORIA
Żyroskop - jest to bryła sztywna, osadzona na osi będącej swobodną osią obrotu i osią największego momentu bezwładności. Jeżeli na wprawiony w szybki ruch obrotowy żyroskop nie działa moment zewnętrzny, to wektor L momentu pędu żyroskopu nie ulega zmianie. Żyroskop wiruje ze stałą prędkością kątową *, a oś obrotu zachowuje stały kierunek w przestrzenni. Wartość liczbowa momentu pędu jest iloczynem momentu bezwładności J względem osi obrotu i wartości liczbowej wektora prędkości kątowej *.
L=J*
Pod działaniem momentu siły zewnętrznych M skierowanego do osi obrotu następuje zmiana wektora momentu pędu.
L- moment pędu
M- moment sił zewnętrznych
dL- wektor zmiany momentu pędu
*- prędkość kątowa precesji
d*- kąt, o który zmienia się oś obrotu żyroskopu w bardzo małym czasie
Zgodnie z rysunkiem i II zasadą dynamiki ruchu obrotowego wektor dL zmiany momentu pędu jest skierowany zgodnie z momentem sił zewnętrznych, a jego wartość liczbowa spełnia zależność.
DL=Mdt=Ld*
Ponieważ wektor dL jest prostopadły do wektora L, wartość momentu pędu nie ulega zmianie, a zamienia się jedynie kierunek tego wektora. W rezultacie występuje ruch obrotowy osi żyroskopu w płaszczyźnie wektorów L, M. Zjawisko to nosi nazwę precesji. Z zależności dL=Mdt=Ld* można obliczyć wartość liczbową wektora prędkości precesji.
![]()
Żyroskop zastosowany w doświadczeniu jest stalowym wirnikiem silnika synchronizowanego 1 zasilanego zasilaczem 2. Silnik zamocowany jest na pręcie stalowym 3. Uchwyt 4 umożliwia obrót pręta dookoła osi pionowej i poziomej. Obciążnik 5 równoważy ciężar żyroskopu.
Moment siły ciężkości wywołany jest przesunięciem obciążnika 5 o masie m z położenia równowagi r0 do innego położenia r.
M=(r-r0)mg
![]()
Wstawiając zależności L=J*, M=(r-r0)mg do
otrzymujemy po przekształceniu
![]()
Precesji mogą towarzyszyć stożkowe ruchy osi żyroskopu zwane mutacjami. Amplituda i okres mutacji rosną przy zwiększaniu momentu bezwładności żyroskopu względem osi prostopadłej do osi symetrii, a maleje ze wzrostem momentu pędu żyroskopu. W skutek tarcia mutacje szybko zanikają.
II OBLICZENIA
L.p |
r0 [m] |
r [m] |
Tn [s] |
*n [rad/s] |
Jn [kgm2] |
1 |
0,275 |
0,295 |
48 |
0,13083 |
0,04237 |
2 |
0,275 |
0,317 |
17 |
0,36941 |
0,03526 |
3 |
0,275 |
0,335 |
12 |
0,523 |
0,0318 |
4 |
0,275 |
0,355 |
7 |
0,8971 |
0,0247 |
5 |
0,275 |
0,375 |
6 |
1,046 |
0,026 |
6 |
0,275 |
0,395 |
5 |
1,256 |
0,0264 |
7 |
0,275 |
0,415 |
4 |
1,57 |
0,024 |
8 |
0,275 |
0,435 |
3,5 |
1,7942 |
0,0247 |
9 |
0,275 |
0,455 |
3 |
2,093 |
0,023 |
10 |
0,275 |
0,475 |
2,5 |
2,512 |
0,022 |
![]()
![]()
![]()
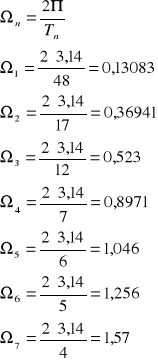
m=1,4kg g=9,8m/s2 *0=2970obr/min=49,5obr/s
![]()

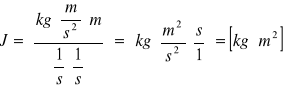
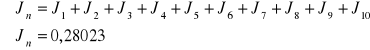
Rachunek błędu metodą rozkładu studenta
*=900 n=10 tn=10 *=900=1,895 - z tablic
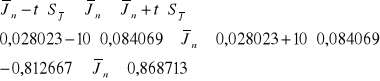
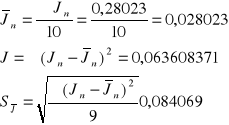
1
4
![]()
![]()
![]()
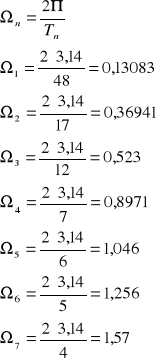
![]()
![]()
![]()
![]()

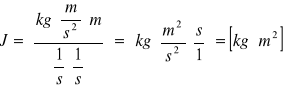
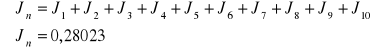
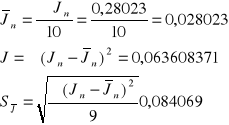
Wyszukiwarka
Podobne podstrony:
Wytrzymałość 1 - lab, Akademia Morska, 2 rok', Semestr III, II rok Wydział Mech, Wytrzymałość Materi
Tabela wyników nr.5, Akademia Morska, 2 rok', Semestr III, II rok Wydział Mech, Wytrzymałość Materia
Elektra Cw.1, Akademia Morska, 2 rok', Semestr III, II rok Wydział Mech, Maszyny elektryczne
mechana, maxwel z bledem, Wydział - Mech
PIERŚC~1, Wydział: MECH
pierŚc~1, Wydział: MECH
pierŚc~1, Wydział: MECH
Tabela do ćw 4 wydymki, Akademia Morska, 2 rok', Semestr III, II rok Wydział Mech, Wytrzymałość Mate
elektra4, Akademia Morska, 2 rok', Semestr III, II rok Wydział Mech, Maszyny elektryczne, Ele cw4
RUCHYB~1, Wydział: MECH
Ochrona środowiska - Kolokfium nr.2 ściąga, Akademia Morska, 2 rok', Semestr III, II rok Wydział Mec
Wytrzymałość 3 - lab, Akademia Morska, 2 rok', Semestr III, II rok Wydział Mech, Wytrzymałość Materi
Ochrona środowiska-ściąga na koło nr.1, Akademia Morska, 2 rok', Semestr III, II rok Wydział Mech, o
Gil 2, Akademia Morska, 2 rok', Semestr III, II rok Wydział Mech, Maszyny elektryczne
Sprawozdanie nr.4, Akademia Morska, 2 rok', Semestr III, II rok Wydział Mech, Wytrzymałość Materiałó
ochrona środowiska - 1 koło, Akademia Morska, 2 rok', Semestr III, II rok Wydział Mech, ochrona środ
Sprawozdanie nr.5, Akademia Morska, 2 rok', Semestr III, II rok Wydział Mech, Wytrzymałość Materiałó
Wytrzymałość 6 - lab, Akademia Morska, 2 rok', Semestr III, II rok Wydział Mech, Wytrzymałość Materi
więcej podobnych podstron