Rozdział 3
RÓWNANIA NIELINIOWE
3.1. Wstęp
W niniejszym rozdziale omówimy algorytmy wyznaczania pierwiastków rzeczywistych jednokrotnych równań nieliniowych. Niech ![]()
będzie funkcją rzeczywistą zmiennej rzeczywistej ![]()
. Pierwiastkiem (zerem) równania
![]()
(3.1)
(lub pierwiastkiem (zerem) funkcji ![]()
) nazywamy każdą wartość ![]()
zmiennej niezależnej ![]()
, dla której ![]()
.
Zagadnienie przybliżonego obliczania pierwiastków definiujemy następująco: dla zadanej dokładności ![]()
należy znaleźć takie![]()
, dla której zachodzi nierówność
![]()
. (3.2)
Przybliżoną wartość pierwiastka funkcji wyznaczamy w dwóch etapach:
najpierw lokalizujemy pierwiastki równania (3.1), tj.
znajdujemy liczbę
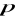
pierwiastków równania,dla każdego pierwiastka
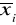
znajdujemy taki przedział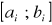
, że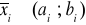
oraz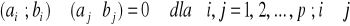
,potem uściślamy przybliżoną wartość pierwiastka, tj. dla zadanego
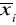
i zadanej dokładności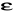
znajdujemy taką wartość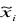
, że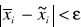
.
3.2. Lokalizacja pierwiastków
Dotychczas nie opracowano algorytmów lokalizacji pierwiastków rzeczywistych dowolnej funkcji ciągłej (odstępstwem od powyższego stwierdzenia jest twierdzenie Sturma, na mocy którego można skonstruować algorytm lokalizacji wszystkich rzeczywistych pierwiastków wielomianu o współczynnikach rzeczywistych).
Na etapie lokalizacji korzystamy z podstawowej wiedzy o funkcjach elementarnych.
Przykład 3.1. Zlokalizować rzeczywiste pierwiastki funkcji
![]()
. (3.3)
Rozwiązanie. Funkcję (3.3) przyrównujemy do zera otrzymując równanie
![]()
,
które następnie przekształcamy do postaci
![]()
.
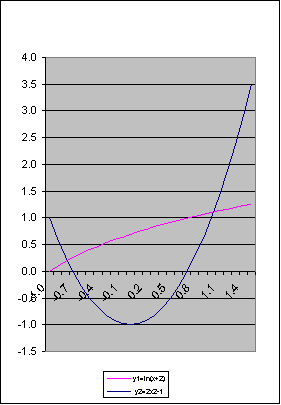
Z łatwością wykonujemy wykresy znanych funkcji ![]()
oraz ![]()
. Odcięte punktów przecięcia się wykresów są pierwiastkami funkcji (3.3). Z tabeli 3.1 oraz wykresu wnioskujemy, że istnieją dwa rzeczywiste pierwiastki funkcji (3.3) leżące w przedziałach ![]()
, ![]()
.
Rys. 3.1. Wykresy funkcji ![]()
i![]()
Tabela 3.1. Lokalizacja pierwiastków funkcji |
|||
|
|
|
|
-1.0 |
0.00000 |
1.00000 |
-1.00000 |
-0.9 |
0.09531 |
0.62000 |
-0.52469 |
-0.8 |
0.18232 |
0.28000 |
-0.09768 |
-0.7 |
0.26236 |
-0.02000 |
0.28236 |
-0.6 |
0.33647 |
-0.28000 |
0.61647 |
-0.5 |
0.40547 |
-0.50000 |
0.90547 |
-0.4 |
0.47000 |
-0.68000 |
1.15000 |
|
|
|
|
... |
... |
... |
... |
|
|
|
|
0.7 |
0.99325 |
-0.02000 |
1.01325 |
0.8 |
1.02962 |
0.28000 |
0.74962 |
0.9 |
1.06471 |
0.62000 |
0.44471 |
1.0 |
1.09861 |
1.00000 |
0.09861 |
1.1 |
1.13140 |
1.42000 |
-0.28860 |
1.2 |
1.16315 |
1.88000 |
-0.71685 |
1.3 |
1.19392 |
2.38000 |
-1.18608 |
1.4 |
1.22378 |
2.92000 |
-1.69622 |
1.5 |
1.25276 |
3.50000 |
-2.24724 |
3.3. Metoda bisekcji (metoda połowienia przedziału)
Zakładamy, że wcześniej został zlokalizowany rzeczywisty pierwiastek funkcji ![]()
, który leży w przedziale ![]()
- zatem ![]()
. Metoda bisekcji jest metodą uściślania przybliżonej wartości pierwiastka, która wymaga założenia:
![]()
. (3.4)
Algorytm 3.1. Uściślanie pierwiastka funkcji ![]()
leżącego w przedziale ![]()
metodą bisekcji.
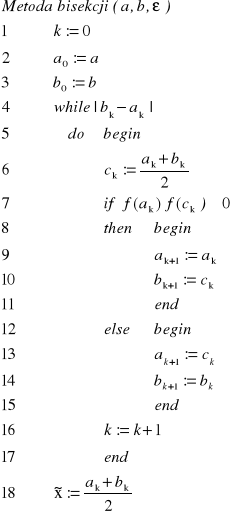
Przykład 3.2. Obliczyć ujemny pierwiastek funkcji
![]()
z dokładnością ![]()
metodą bisekcji.
Rozwiązanie. W przykładzie 3.1 pokazano, że ujemny pierwiastek funkcji (3.3) leży w przedziale [-0.8 ; -0.7]. Obliczenia kolejnych kroków metody bisekcji są zestawione w tabeli 3.2.
Tabela 3.2. Wyznaczanie ujemnego pierwiastka funkcji |
|||||
|
|
|
|
||
z dokładnością 10-5 metodą bisekcji. |
|
|
|||
|
|
|
|
|
|
|
-0.800000 |
|
-0.700000 |
|
1.0E-03 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
-0.800000 |
-0.700000 |
-0.750000 |
-9.6E-03 |
1.0E-01 |
1 |
-0.800000 |
-0.750000 |
-0.775000 |
-1.7E-04 |
5.0E-02 |
2 |
-0.800000 |
-0.775000 |
-0.787500 |
4.7E-03 |
2.5E-02 |
3 |
-0.787500 |
-0.775000 |
-0.781250 |
1.1E-03 |
1.3E-02 |
4 |
-0.781250 |
-0.775000 |
-0.778125 |
2.4E-04 |
6.2E-03 |
5 |
-0.778125 |
-0.775000 |
-0.776563 |
4.7E-05 |
3.1E-03 |
6 |
-0.776563 |
-0.775000 |
-0.775781 |
6.1E-06 |
1.6E-03 |
7 |
-0.775781 |
-0.775000 |
-0.775391 |
-2.2E-07 |
7.8E-04 |
8 |
-0.775781 |
-0.775391 |
-0.775586 |
8.3E-07 |
3.9E-04 |
9 |
-0.775586 |
-0.775391 |
-0.775488 |
1.3E-07 |
2.0E-04 |
10 |
-0.775488 |
-0.775391 |
-0.775439 |
6.8E-09 |
9.8E-05 |
11 |
-0.775439 |
-0.775391 |
-0.775415 |
-2.0E-09 |
4.9E-05 |
12 |
-0.775439 |
-0.775415 |
-0.775427 |
-5.3E-10 |
2.4E-05 |
13 |
-0.775439 |
-0.775427 |
-0.775433 |
2.1E-10 |
1.2E-05 |
14 |
-0.775433 |
-0.775427 |
-0.775430 |
-3.5E-11 |
6.1E-06 |
3.4. Metoda stycznych (metoda Newtona-Raphsona)
Metoda stycznych jest inną metodą uściślania przybliżonej wartości pierwiastka. Zakładamy zatem, że wcześniej został zlokalizowany rzeczywisty pierwiastek funkcji ![]()
leżący w przedziale ![]()
; a zatem ![]()
. Metoda stycznych wymaga silniejszych niż metoda bisekcji założeń odnośnie funkcji ![]()
, a mianowicie:
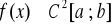
, (3.5)dla każdego
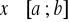
albo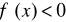
albo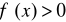
(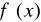
nie zmienia znaku w przedziale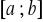
), (3.6)dla każdego
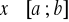
albo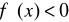
albo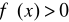
(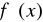
nie zmienia znaku w przedziale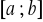
). (3.7)
Algorytm 3.2. Uściślanie pierwiastka funkcji ![]()
leżącego w przedziale ![]()
metodą Newtona-Raphsona.
Metoda Newtona-Raphsona(![]()
)
W charakterze
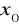
wybieramy ten kraniec przedziału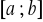
(tzn. albo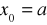
,
albo ![]()
), który spełnia warunek:![]()
. (3.8)
Wyznaczamy:
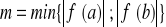
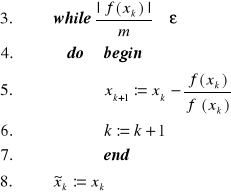
(3.9)
Ciąg wygenerowany według reguł (3.8)÷(3.9) nosi nazwę procesu Newtona-Raphsona. Jego własności zostały sformułowane w poniższym twierdzeniu.
Twierdzenie 3.1. Jeżeli funkcja ![]()
spełnia założenia (3.5)÷(3.7), to proces Newtona-Raphsona ma następujące własności:
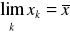
(proces jest zbieżny do pierwiastka funkcji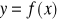
leżącego w przedziale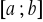
, (3.10)ciąg (3.8)÷(3.9) jest ściśle monotoniczny, tzn. albo
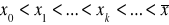
albo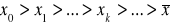
(3.11)k-ty wyraz procesu spełnia nierówność:
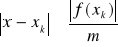
, (3.12)
gdzie ![]()
.
Przykład 3.3. Obliczyć ujemny pierwiastek funkcji
![]()
z dokładnością ![]()
metodą Newtona-Raphsona.
Rozwiązanie. W przykładzie 3.1 pokazano, że ujemny pierwiastek funkcji (3.3) leży w przedziale ![]()
. Na początku wykażemy, że funkcja (3.3) spełnia w przedziale ![]()
warunki (3.5)÷(3.7).
Dla
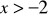
funkcja (3.3) jest ciągła i posiada ciągłe pochodne wszystkich rzędów.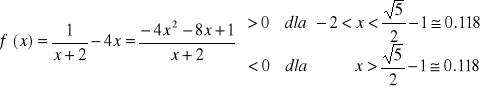
Zatem w przedziale [-0.8 ; -0.7] ![]()
.
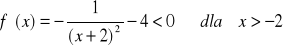
.
Zatem funkcja (3.3) spełnia w przedziale [-0.8 ; -0.7] warunki (3.5)÷(3.7) i w związku z tym możemy zastosować metodę stycznych do uściślenia przybliżonej wartości pierwiastka.
Wyznaczamy ![]()
oraz ![]()
. Z tabeli 3.1 odczytujemy
![]()
, ![]()
. Więc ![]()
, ponieważ ![]()
. Następnie obliczamy
![]()
.
Wartości kolejnych iteracji metody stycznych są podane w tabeli 3.3.
Tabela 3.3. Wyznaczanie ujemnego pierwiastka funkcji |
|
||||
|
|
|
|
||
z dokładnością 10-5 metodą stycznych. |
|
|
|||
|
|
|
|
|
|
|
-0.800000 |
|
3.569231 |
|
1.0E-03 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
-0.800000 |
-0.097678 |
4.033333 |
-0.024218 |
2.7E-02 |
1 |
-0.775782 |
-0.001374 |
3.919977 |
-0.000350 |
3.8E-04 |
2 |
-0.775432 |
0.000000 |
3.918341 |
0.000000 |
8.0E-08 |
3.5. Metoda iteracji prostej
Metoda iteracji prostej jest metodą uściślania przybliżonej wartości pierwiastka. Zakładamy zatem, że wcześniej został zlokalizowany pierwiastek funkcji ![]()
i leży w przedziale ![]()
; zatem ![]()
. Metoda iteracji prostej składa się z dwóch etapów.
Najpierw równanie
![]()
(3.13)
przekształcamy do równoważnej postaci
![]()
(3.14)
(takie przekształcenie jest zawsze wykonalne i zazwyczaj można to dokonać kilkoma sposobami).
Wybieramy z przedziału
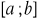
przybliżenie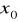
. Kolejne iteracje obliczamy ze wzoru
![]()
(3.15)
W poniższym twierdzeniu zostały sformułowane warunki wystarczające zbieżności ciągu (3.15) do pierwiastka funkcji (3.13) leżącego w przedziale ![]()
.
Twierdzenie 3.2. Niech funkcja ![]()
będzie określona, ciągła i różniczkowalna w przedziale domkniętym ![]()
oraz ![]()
dla każdego ![]()
. Jeśli nierówność
![]()
zachodzi dla każdego ![]()
,
to
proces (3.15) jest zbieżny niezależnie od wyboru
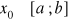
oraz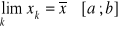
zachodzą nierówności
![]()
![]()
(3.16)
Algorytm 3.3. Uściślanie pierwiastka funkcji ![]()
leżącego w przedziale ![]()
metodą iteracji prostej.
Metoda iteracji prostej(a, b, q, ![]()
)
Równanie (3.13) przekształcamy do takiej postaci równoważnej (3.14), która spełnia założenia twierdzenia 3.2.
W charakterze przybliżenia zerowego wybieramy dowolny
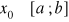
, np.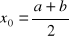
.
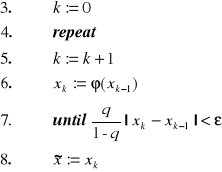
Przykład 3.4. Obliczyć ujemny pierwiastek funkcji
![]()
z dokładnością ![]()
metodą iteracji prostej.
Rozwiązanie. W przykładzie 3.1 pokazano, że ujemny pierwiastek funkcji (3.3) leży w przedziale ![]()
a dodatni w przedziale ![]()
. Poszukamy obecnie przekształcenia równania
![]()
do równoważnej postaci typu (3.14), spełniającej założenia twierdzenia 3.2. Równanie możemy przekształcić w następujący sposób
![]()
.
Dla tego przedstawienia mamy
![]()
.
Ta funkcja jest:
w przedziale
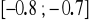
monotonicznie malejąca, zatem dla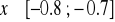
zachodzi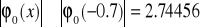
;w przedziale
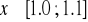
monotonicznie rosnąca, zatem dla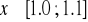
zachodzi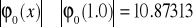
.
W obydwu przedziałach ![]()
, więc utworzony proces (3.15) przez odwzorowanie ![]()
jest rozbieżny.
Równanie ![]()
może być przedstawione w równoważnej postaci jako para równań
![]()
![]()
Dla obydwu funkcji mamy
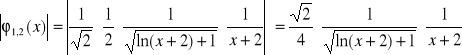
.
Dla ![]()
funkcja ![]()
jest monotonicznie malejąca, zatem
![]()
.
W związku z tym, w procesie iteracyjnym użyjemy
funkcji
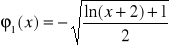
dla wyznaczenia przybliżonej wartości pierwiastka z przedziału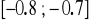
,funkcji
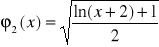
dla wyznaczenia przybliżonej wartości pierwiastka z przedziału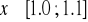
.
Za ![]()
przyjęto:
![]()
dla pierwiastka z przedziału ![]()
,
![]()
dla pierwiastka z przedziału ![]()
.
Wartości kolejnych iteracji metody iteracji prostej są podane w tabeli 3.4.
Tabela 3.4. Wyznaczanie pierwiastków funkcji |
|
||||||||
|
|
|
|
|
|
||||
metodą iteracji prostej, z dokładnością 10-5. |
|
||||||||
|
|
|
|
|
|
|
|||
|
-0.75000 |
|
|
|
1.05000 |
|
|||
|
0.27096 |
|
|
|
0.08135 |
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
0 |
-0.75000 |
|
|
0 |
1.05000 |
|
|||
1 |
-0.78203 |
8.6E-02 |
|
1 |
1.02838 |
5.8E-02 |
|||
2 |
-0.77369 |
2.2E-02 |
|
2 |
1.02665 |
4.7E-03 |
|||
3 |
-0.77589 |
5.9E-03 |
|
3 |
1.02651 |
3.7E-04 |
|||
4 |
-0.77531 |
1.6E-03 |
|
4 |
1.02650 |
3.0E-05 |
|||
5 |
-0.77546 |
4.1E-04 |
|
5 |
1.02650 |
2.4E-06 |
|||
6 |
-0.77542 |
1.1E-04 |
|
|
|
|
|||
7 |
-0.77543 |
2.8E-05 |
|
|
|
|
|||
8 |
-0.77543 |
7.5E-06 |
|
|
|
|
|||
3.6. Efektywność metod przybliżonego obliczania pierwiastków funkcji
Obecnie naszym celem jest porównanie metod uściślania przybliżonej wartości jednokrotnego pierwiastka funkcji ![]()
. Zakładamy, że metoda iteracyjna generuje ciąg ![]()
kolejnych przybliżeń zbieżny do pierwiastka ![]()
funkcji ![]()
. Każdej metodzie można przyporządkować liczbę ![]()
zwaną wykładnikiem zbieżności metody (lub rzędem metody), oraz stałą ![]()
, zwaną stałą asymptotyczną błędu metody, które spełniają warunek
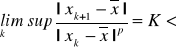
. (3.17)
Rząd metody i stała ![]()
charakteryzują szybkość zbieżności metody iteracyjnej: ciąg kolejnych przybliżeń ![]()
jest tym szybciej zbieżny do pierwiastka, im większy jest rząd metody i im mniejsza jest stała asymptotyczna błędu. Spośród tych dwóch wielkości istotniejszą rolę odgrywa wykładnik zbieżności ![]()
. Przykładowo,
Dla metody iteracji prostej: ![]()
oraz ![]()
,
Dla metody stycznych: ![]()
oraz ![]()
.
3.7. Zadania
Zad. 3.1. Liczba iteracji w metodzie bisekcji
Wykazać, że dla wyznaczenia przybliżonej wartości pierwiastka leżącego w przedziale ![]()
z dokładnością![]()
trzeba w metodzie bisekcji wykonać ![]()
iteracji.
Zad. 3.2. Kryterium zakończenia obliczeń w metodzie Newtona-Raphsona
Udowodnić, że dla procesu Newtona-Raphsona zachodzi nierówność
![]()
,
gdzie
![]()
, ![]()
.
Nierówność tę można wykorzystać jako kryterium zakończenia obliczeń w metodzie Newtona-Raphsona.
Zad. 3.3. Kryterium zakończenia obliczeń w metodzie iteracji prostej
Udowodnić, że jeśli proces iteracji prostej jest zbieżny, to zachodzi nierówność
![]()
,
Nierówność tę można wykorzystać jako kryterium zakończenia obliczeń w metodzie iteracji prostej.
Zad. 3.4. Podprogram obliczania pierwiastka
Zakładamy, że dysponujemy narzędziem obliczeniowym wykonującym 5 działań zmiennoprzecinkowych: dodawanie, odejmowanie, mnożenie, dzielenie i potęgowanie. Opracować algorytm obliczania ![]()
dla dowolnej dodatniej liczby rzeczywistej ![]()
i dowolnego naturalnego ![]()
.
Wskazówka. Oznaczyć![]()
. Równość ta jest równoważna równości ![]()
. Oznacza to, że należy znaleźć pierwiastek funkcji ![]()
. Dowieść, że do znalezienia pierwiastka tej funkcji można zastosować metodę Newtona-Raphsona.
Zad. 3.5. Stosując metodę bisekcji obliczyć z dokładnością ε rzeczywiste pierwiastki poniższych funkcji
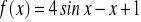
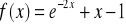
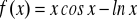
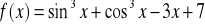
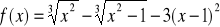
.
Zad. 3.6. Stosując metodę Newtona-Raphsona obliczyć z dokładnością ε rzeczywiste pierwiastki poniższych funkcji.
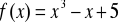
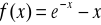
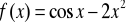
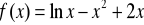
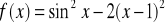
.
Zad. 3.7. Stosując metodę iteracji prostej obliczyć z dokładnością ε rzeczywiste pierwiastki poniższych funkcji.
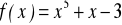
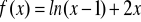
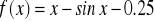
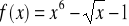
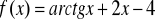
.
Wyszukiwarka
Podobne podstrony:
Podstawy zarządzania wykład rozdział 05
Podstawy zarządzania wykład rozdział 14
Podstawy marketingu, marketing wykłady, Rozdział 1 - podstawowe pojęcia i cele marketingu- mix
Podstawy zarządzania wykład rozdział 04
Podstawy zarządzania wykład rozdział 03
Podstawy zarządzania wykład rozdział 06
Wykład 3 3 rozdzielczość FFT
Podstawy zarządzania wykład rozdział 16
Projektowanie sieci LAN WAN wykład 7 Rozdzielnie i okablowanie
Podstawy zarządzania wykład rozdział 13
Podstawy zarządzania wykład rozdział 07
Podstawy zarządzania wykład rozdział 12
Podstawy zarządzania wykład rozdział 08
Podstawy zarządzania wykład rozdział 11
Podstawy zarządzania wykład rozdział 15
Podstawy zarządzania wykład rozdział 10
Podstawy zarządzania wykład rozdział 05
Podstawy zarządzania wykład rozdział 14
Wykład I- Wprowadzenie, Rozdział 2 - Hipotezy przepływu
więcej podobnych podstron