POLITECHNIKA ŚLĄSKA

W GLIWICACH

WYDZIAŁ ELEKTRYCZNY

Kierunek : elektrotechnika.

Studia wieczorowe

Rok akademicki:1998/99.

DYFRAKCJA ŚWIATŁA

Sekcja 5:

Dziurosz Jerzy

Grudzień Marcin

DYFRAKCJA ŚWIATŁA

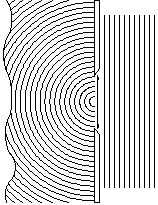
Dyfrakcja fal (lub ugięcie fal) jest w szerokim sensie zespołem zjawisk związanych z odstępstwami od praw optyki geometrycznej podczas rozchodzenia się fal w ośrodkach niejednorodnych. W węższym znaczeniu - dyfrakcja fali jest pewnym odstępstwem od praw optyki geometrycznej przy rozprzestrzenianiu się fal lokalnie płaskich w ośrodkach jednorodnych. Wskutek dyfrakcji pojawiają się dodatkowe kierunki rozchodzenia się fal, nieprzewidziane przez optykę geometryczną. Przy przejściu światła przez szczelinę powinniśmy obserwować powstawanie cienia. W rzeczywistości obserwujemy pod pewnymi kątami smugi jaśniejsze i ciemniejsze. Zjawisko dyfrakcji jest charakterystyczne dla wszystkich rodzajów fali, jednak możliwość obserwacji efektów dyfrakcyjnych maleje ze wzrostem częstotliwości.

Zjawisko dyfrakcji zostało zaobserwowane przez uczonego włoskiego F. M. Grimaildiego w roku 1665. Próbę wyjaśnienia tego zjawiska podjął Newton, jednak dopiero T. Young w 1807 r. opracował teorię dyfrakcji opartą na połączeniu właściwej dyfrakcji z interferencją fal.

Zgodnie z zasadą Huyghensa każdy element czoła fali może być uważany za nowe źródło fal (kulistych). Young przyjął dodatkowo, że wzdłuż czoła fali zachodzi poprzeczne przekazywanie amplitudy drgań. Na rysunku pokazano schemat doświadczeni Younga. Światło lampy łukowej przechodzi przez szczelinę szerokości 0.25 mm. i pada na ekran z dwoma otworami o średnicy 0.1 mm rozsuniętymi o 0.7 mm. Na ekranie odległym o 5 metrów obserwuje się wynik interferencji fali kulistych. Obydwie szczeliny można potraktować jako źródła drgające synchronicznie, więc różnica faz dwóch fali docierających

do punktu A jest wynikiem różnicy przebytej drogi.

Wzmocnienie fali zajdzie wówczas, gdy różnica faz wyniesie 2
k (k jest liczbą całkowitą). Stąd wynika warunek wzmocnienia:

W doświadczeniu Younga stosując światło białe zaobserwujemy prążki barwne, nakładające się na siebie, a liczba rzędów nie będzie większa od 10. Prążki w doświadczeniu Younga nie są zlokalizowane na ekranie, a obraz uzyska się przy dowolnej odległości ekranu od źródła światła. Same prążki są stosunkowo słabe. Znacznie silniejszy efekt interferencyjno - dyfrakcyjny obserwuje się w doświadczeniu H. Lloyda. Zastosowanie zwierciadła płaskiego powoduje, że pozorny obraz jednej szczeliny emuluje drugie źródło światła. Interferencję światła można zaobserwować w wielu innych przypadkach, np. przy padaniu światłą na cienką błonę. W naszym przypadku skoncentrujmy się jednak na dyfrakcji światła.

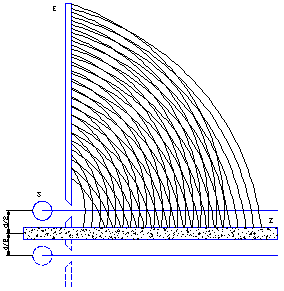
Zgodnie z interpretacją Younga, powstawanie fal ugiętych ma charakter lokalny i zachodzi w okolicy granicy cienia za krawędzią przesłony lub w obszarze oświetlonym. W pierwszym przypadku ugięcie wystąpi w skutek przekazywania amplitudy drgań wzdłuż walcowych powierzchni falowych za granicą cienia. W przypadku drugim - fale walcowe wysyłane są z brzegu otworu. Zaburzenie w pewnym miejscu za otworem może być traktowane jako interferencja fali podlegającej prawom optyki geometrycznej i fali ugiętej. Powyższa teoria dyfrakcji nie wyjaśnia faktu, że obraz dyfrakcyjny jest taki sam dla ostrego i zaokrąglonego brzegu przeszkody. Teoria nie wyjaśnia też faktu niewystępowania dyfrakcji w kierunku wstecznym.

Fresnel uzupełnił zasadę Huyghensa interpretując zjawiska dyfrakcyjne jako wynik interferencji fal pochodzących z nie skończonej liczby źródeł elementarnych rozmieszczonych w całej płaszczyźnie otworu. Amplitudy i fazy tych fal są proporcjonalne do amplitudy i fazy fali padającej na otwór. Zgodnie z twierdzeniem Babineta, otwór lub przesłona tego samego kształtu i tej samej wielkości dają taki sam obraz dyfrakcyjny.

Celem poglądowego przedstawienia dyfrakcji w punkcie A za otworem Frensel wprowadził podział płaszczyzny otworu na pierścieniowe, półfalowe strefy. Promienie tych stref dobiera się tak, aby odległość kolejnych okręgów od punktu A różniły się o połowę długości fali.

Promień k-tej strefy obliczmy stosując wzór Pitagorasa.

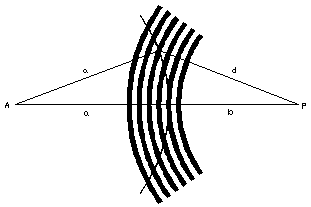
ponieważ x jest znacznie mniejsze od a.

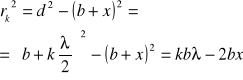
Z drugiej strony mamy:

Porównując prawe strony wyrażeń otrzymujemy:

skąd: Wielkość stref Fresnela

i po podstawieniu otrzymujemy ostateczne:

Można pokazać, że pola powierzchni wszystkich stref są prawie takie same:

Różnica faz fali pochodzących z sąsiednich stref wynosi
/2. Fale te są spójne i w wyniku interferencji otrzymujemy wzmocnienie lub osłabienie fali wypadkowej:

Powyższe równanie zapisujemy w postaci:

Amplituda fali z k-tej strefy zależy od k, ponieważ:

• Odległości stref od źródła wzrastają, więc amplitudy powoli maleją

• Wzrasta nachylenie promienia do powierzchni strefy i zmniejsza się natężenie promieniowania w stosunku do kierunku prostopadłego.

• 
  Amplituda zależy od powierzchni strefy (pokazaliśmy, że powierzchnie te są prawie równe, jednak przy dokładnej analizie zaobserwujemy powolny wzrost ze wzrostem liczby k).

Płytki strefowe Fresnela.

Wpływ pierwszego czynnika dokładnie równoważy działanie trzeciego czynnika, a więc:

Zmiany są niewielkie i dla sąsiednich sfer zachodzi:

Natężenie fali zależy więc jedynie od amplitudy pierwszej strefy, bowiem A=A/2.

Jeżeli światło przechodzi przez kolisty otwór o promieniu mniejszym lub równym promieniowi pierwszej strefy Fresnela, to w punkcie leżącym na osi otworu otrzymamy wzmocnienie oświetlenia (dla równych promieni nawet czterokrotnie). Przy dalszym wzroście promieniowania otworu maleje oświetlenie w analizowanym punkcie i gdy otwór będzie odpowiadał dwóm strefom Fresnela, to w naszym punkcie będzie ciemno. Fakt zwiększanie natężenia światła dla otworów o odpowiednich promieniach został wykorzystany w tzw. płytkach strefowych z zaczernionymi strefami parzystymi (lub nieparzystymi).

Dla wąskiej równoległej szczeliny, natężenia kolejnych jasnych prążków maleją bardzo szybko ze wzrostem rzędu prążka. Przykładowo dla szerokości szczeliny 0.3 mm natężenie pierwszego prążka wynosi I₁=0.45 I₀, a drugiego już I₂=0.016 I₀.

WYZNACZANIE STAŁEJ SIATKI DYFRAKCYJNEJ

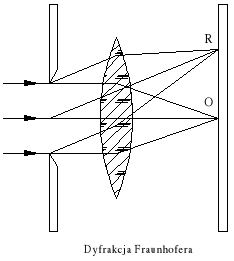
Zjawiska dyfrakcyjne można podzielić na dwie grupy zależnie od odległości szczeliny od źródła i ekranu. Jeśli przynajmniej jedna z tych odległości jest skończona, to mamy do czynienia z dyfrakcją Fresnela. Dyfrakcja Fraunhofera zachodzi wówczas, gdy zarówno źródło, jak i ekran są w nieskończenie wielkich odległościach od szczeliny. W takim przypadku na szczelinę pada światło równoległe i na ekranie zaobserwuje się obraz dyfrakcyjny jedynie przy zastosowaniu soczewki skupiającej ustawionej w odległości ogniskowej od ekranu.

W 1823 r. Fraunhoffer zbudował siatkę dyfrakcyjną złożoną z drutów mosiężnych o średnicy 50 mm naciągniętych na dwie śruby o skoku 150 mm. Taka siatka miała na 1 mm. 7 drutów. Później stosując rowki w warstwach złota i tłuszczu uzyskał siatkę z 80 szczelinami przypadającymi na 1mm. Rowland uzyskał siatkę o liczbie 800 rys na 1 mm. Współczesne siatki wykonuje się na kliszach fotograficznych stosując dyfrakcję światła laserowego.

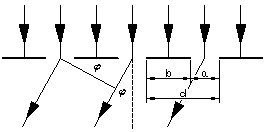
Niech na siatkę dyfrakcyjną pada prostopadle fala płaska o długości l. Szerokość szczeliny wynosi a, a ich wzajemna odległość b. Ugięte fale, jako spójne, interferują dając w pewnych kierunkach wzmocnienie natężenia, w innych zaś - osłabienie. Wzmocnienie nastąpi gdy różnica dróg optycznych jest wielokrotnością długości fali, co daje:

Wielkość d =a+b nazywamy stałą siatki dyfrakcyjnej, a k - rzędem prążka dyfrakcyjnego. Powyższy wzór zapisujemy więc w postaci:

Dla światła monochromatycznego uzyskuje się obraz dyfrakcyjny (a ściślej inerferencyjno - dyfrakcyjny) w postaci szeregu jasnych prążków rozłożonych symetrycznie po obu stronach prążka centralnego leżącego na przedłużeniu wiązki światła. Stosując zaś światło nie monochromatyczne uzyskamy prążki barwne, nakładające się częściowo na siebie w miarę wzrostu rzędu k.

Natężenie prążków zależy od kwadratu całkowitej liczby szczelin N i rzędu prążka, i tak dla prążka centralnego mamy:

gdzie C - współczynnik proporcjonalności.

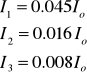
Natężenia kolejnych prążków są coraz słabsze:

Siatki dyfrakcyjne stosuje się w spektrografach do pomiaru długości fali. Miarą jakości siatki jest tzw. zdolność rozszczepiająca:

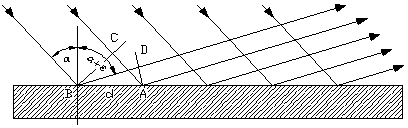
gdzie dl jest najmniejszym przedziałem różnicy długości fali dającym się rozróżnić w k-tym prążku. Wielkość ta nie zależy od stałej siatki, lecz od całkowitej liczby szczelin.

Siatka odbiciowa

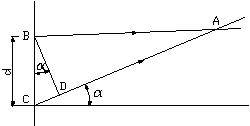
Zjawisko interferencji fali dyfrakcyjnych można również obserwować w świetle odbitym. Jeśli na płytkę, na której nacięto równoległe rysy, pada wiązka światła równoległego pod kątem a, to różnica dróg dwóch sąsiednich promieni ugiętych wynosi:

co daje nam warunek wzmocnienia:

Takie siatki, będące często kopiami siatek Rowlanda, mają większą zdolność rozszczepiającą od zwykłych siatek dyfrakcyjnych.

POMIAR DŁUGOŚCI ŚWIATŁA LASEROWEGO

Elektrodynamika kwantowa przewiduje, że naładowane cząstki (np. elektrony) mogą emitować lub pochłaniać pojedyncze fotony, a prawdopodobieństwo tych zjawisk można obliczyć stosując równanie Schrodingera.

Elektron znajdujący się w stanie energetycznym wyższym niż podstawowy, przechodzi do stanu podstawowego emitując foton. Takie zjawisko nazywamy emisją spontaniczną. Zjawisko absorpcji zwane też pompowaniem optycznym, polega na przejściu elektronu na wyższy poziom energetyczny przy przejściu promieniowania przez substancję. Zgodnie z teorią Einsteina, tym zjawiskom towarzyszy promieniowanie wymuszone, przy ma ono identyczne właściwości z promieniowaniem przechodzącym przez substancję i wywołującym promieniowanie wymuszone. Emitowane fotony mają tą samą energię co fotony wymuszające i będąc z nimi spójne powodują zwiększenie amplitudy bez zmiany częstotliwości, kierunku rozchodzenia, fazy i polaryzacji.

W laserach (lub maserach - w zakresie mikrofalowym) wykorzystano właśnie zjawisko emisji wymuszonej. Taki wzmacniacz (i generator) otrzymamy w tedy, gdy zmniejszymy prawdopodobieństwo procesów energii spontanicznej i absorpcji zwiększając jednocześnie prawdopodobieństwo zaistnienia procesów emisji wymuszonej. Stan taki, zwany inwersją obsadzeń poziomów energetycznych, wystąpi podczas zakłócenia stanu równowagi termodynamicznej substancji czynnej. Wówczas większość atomów uczestniczących w aktach wzmocnienia będzie miało energię większą od energii w stanie podstawowym, mniej zaś - energię mniejszą. Zgodnie z teorią Boltzmanna odpowiadało by to stanowi o ujemnej temperaturze.

Jeśli w substancji z inwersją obsadzeń energetycznych wytworzy się warunki umożliwiające powstawanie drgań samowzbudnych, to powstanie generator kwarcowy, czyli laser. Do układu wzmacniacza kwantowego wprowadza się silnie dodatnie sprzężenie zwrotne. Część wypromieniowanej energii powraca do powodując następne akty emisji wymuszonej w substancji czynnej. Promieniowanie elektromagnetyczne powstające w wyniku emisji wymuszonej jest spójne z promieniowaniem wywołującym tą emisję, więc sprzężenie zwrotne powoduje ciągłe przekazywanie energii od substancji znajdującej się w stanie inwersji obsadzeń do pola elektromagnetycznego o określonym rodzaju drgań.

W zakresie mikrofalowym substancję czynną umieszcza się we wnęce rezonansowej prawie całkowicie zamkniętej o wymiarach porównywalnych z długością fali generowanego promieniowania. Rezonatory w zakresie optycznym mają wymiary znaczenie większe od długości fali i rolę tę spełniają dwa równoległe zwierciadła płaskie (lub sferyczne) umieszczone naprzeciwko siebie. Odległości pomiędzy zwierciadłami wynosi:

gdzie a - współczynnik załamania ośrodka, k - liczba naturalna. Kwant światła padając prostopadle na powierzchnie zwierciadeł odbija się kolejno od nich przechodząc wielokrotnie przez substancję czynną i wywołując kolejne akty emisji wymuszonej. Warunkiem powstania drgań samowzbudnych jest tzw. warunek progowy, gdy moc promieniowania wywołanego emisją wymuszoną jest większa od mocy traconej w obwodzie.

Rodzaje laserów zależą od zastosowanej metody wytwarzania stanu inwersji obsadzeń poziomów energetyczntch:

1. Pompowanie za pomocą promieniowania elektromagnetycznego o innej częstotliwości, niż ta dla której zachodzi generacja.

2. Zderzenia niesprężyste elektronów z atomami lub atomów z atomami.

3. Wstrzykiwanie nośników ładunków przez złącze półprzewodnikowe p-n.

4. Separacja przestrzenna cząsteczek znajdujących się w stanie o większej energii.

5. Dwupoziomowe masery krystaliczne

Największe znaczenie posiadają lasery impulsowe zbudowane na ciele stałym, lasery gazowe oraz lasery półprzewodnikowe.

Na rysunku pokazano schemat budowy lasera zbudowanego na ciele stałym. Pręt wykonany z substancji czynnej (Al₂O₂ z dodatkiem Cr₂O₃ - rubin, CaF₂, CaWO₄, YAG lub szkło optyczne) posiada optycznie polerowane powierzchnie czołowe stanowiące układ rezonatorów optycznych. Pręt umieszcza się wewnątrz lampy błyskowej zasilanej z baterii kondensatorów. Całość zamknięta jest w obudowie z układem chłodzącym. Podczas jednego aktu laserowego emitowana jest energia rzędu 100J, co przy czasie akcji ok. 1 ms. daje moc do kilkudziesięciu kW. W laserach z granatem litowo-aluminiowym (YAG) uzyskuje się quasi-ciągłą emisję promieniowania. W laserze o modulowanej dobroci rezonatora można wytworzyć gigantyczne impulsy o mocy GW i czasie rzędu ns.

W laserze półprzewodnikowym elementem czynnym jest dioda półprzewodnikowa wykonana najczęściej z arsenku galu, arsenku indu lub fosforku indu. Złącze p-n jest prostopadłe do ścianek zewnętrznych diody, pełniących rolę rezonatora optycznego. Jedna ze ścianek pokryta jest dielektrykiem i odbija całkowicie światło, a przez drugie zwierciadło częściowo przepuszczalne promieniowanie laserowe wydostaje się na zewnątrz. Cechą charakterystyczną laserów półprzewodnikowych jest ich mały rozmiar, duża sprawność (duża moc przypadająca na jednostkę objętości) i prosta konstrukcja.

Laser gazowy zbudowany jest z rury kwarcowej wypełnionej gazem lub mieszaniną gazów pod obniżonym ciśnieniem i pary zwierciadeł płaskich o nierównomierności powierzchni porównywalnej z długością fali. Źródłem energii wzbudzenia atomów lub jonów może być generator wysokiej częstotliwości, generator mikrosekundowy, źródło prądu stałego lub generator ultra dźwiękowy. W laserze helowo-neonowym pompowanie optyczne polega na wzbudzeniu atomów w wyniku zderzeń z elektronami lub na wymianie energii pomiędzy wzbudzonymi atomami helu i nie wzbudzonymi atomami neonu. W ten sposób uzyskuje się stan inwersji obsadzeń poziomów energetycznych. Wzbudzone atomy neonu w wyniku emisji wymuszonej przechodzą w niższe stany energetyczne. Oprócz światła czerwonego o długości 632,8 nm można otrzymać promieniowanie podczerwone o długościach fali 1150 nm i 3390 nm. Atomy helu nie biorą bezpośrednio udziału w akcji laserowej, lecz poprawiają sprawność pompowania optycznego dzięki koincydencji z odpowiednimi stanami energetycznymi neonu. Oprócz laserów He-Ne stosuje się lasery argonowe i lasery wypełnione dwutlenkiem węgla.

WYZNACZANIE SZEROKOŚĆI SZCZELINY

Schemat zestawu do nadanie zjawiska dyfrakcji światła laserowego na wąskiej szczelinie pokazano na rysunku. Źródłem światła jest laser helowo-neonowy produkcji rosyjskiej. Badana szczelina umieszczona jest na stoliku z podziałką. Zastosowanie prowadnicy pozwala tak ustawić szczelinę, aby jej płaszczyzna była prostopadła do osi zestawu. Odległość szczeliny od detektora można odczytać bezpośrednio na podziałce (pacząc od strony detektora).

Detektorem jest fotorezystor zasilany prądem stałym, a natężenie płynącego prądu mierzymy multimetrem typu M-4650CR firmy METEX. Natężenie prądu zależy od natężenia oświetlenia. Detektror umieszczony jest na wysięgniku przesuwnego suportu. Niskoobrotowy silnik indukcyjny z wielostopniową przekładnią zapewnia stały, określony przesuw suportu. Diody luminescencyjne na obudowie przekładni wskazują kierunek przesuwu. Do zmiany kierunku przesuwu służy przełącznik, a wyłącznik silnika umieszczono po silnikiem. Wyłączniki krańcowe kontrolują zakres przesuwu suportu.

W ćwiczeniu zastosowano miernik uniwersalny firmy METEX z adapterem umożliwiającym bezpośrednie połączenie z wejściem szeregowym RS-232C komputera PC/AT. Miernik sterowany jest programem dołączonym do miernika.

PRZEBIEG ĆWICZEŃ

Wyznaczanie stałej siatki dyfrakcyjnej

1. Sprawdzamy poprawność ustawienia kolimatora i lunety spektrometru. Obraz wąskiej szczeliny powinien być ostry, a luneta ustawiona „na nieskończoność”.

2. Siatkę dyfrakcyjną umieszczamy na stoliku obrotowym spektrometru. Płaszczyzna siatki powinna być prostopadła do osi przyrządu,

3. Obracając lunetką z okularem (względem osi przyrządu) doprowadzamy do pokrycia się krzyża pomiarowego z kolejnymi prążkami dyfrakcyjnymi. Notujemy kąty ugięcia dla trzech rzędów (na lewo i prawo od prążka zerowego).

4. Pomiary powtarzamy pięciokrotnie.

5. Obliczamy średnie wartości kątów ugięcia dla poszczególnych rzędów.

Tabelka pomiarowa:

Dokładność pomiaru 20'

Lp.	n = 1		n = 2		n = 3
1	-6°40'	6°40'	-13°00'	13°20'	-20°00'	20°20'
2	-6°20'	6°40'	-13°20'	13°20'	-20°20'	20°20'
3	-6°20'	6°40'	-13°10'	13°20'	-20°20'	20°20'
4	-6°00'	6°20'	-13°00'	13°20'	-20°20'	20°00'
5	-6°00'	6°20'	-13°00'	13°20'	-20°20'	20°00'
Śr.	-6°16'	6°32'	-13°06'	13°20'	-20°16'	20°12'

Według wzoru wyliczamy następujące wartości kąta ugięcia. Następnie stosując średnią arytmetyczną obliczono średnie kąty ugięcia dla kolejnych prążków.

Rząd prążka - n	n = 1	n = 2	n = 3
numer pomiaru	Kąt ugięcia	kąt ugięcia	kąt ugięcia
1	6°40'	13°10'	20°10'
2	6°30'	13°20'	20°20'
3	6°30'	13°15'	20°20'
4	6°10'	13°10'	20°10'
5	6°10'	13°10'	20°10'
Średni kąt ugięcia	6°24'	13°13'	20°14'

6. Obliczamy stałą siatki dyfrakcyjnej. Przeprowadzamy rachunek błędów. Wyniki odpowiadające kolejnym rzędom ugięcia należy uśrednić stosując metodę średniej ważonej

Pomiary dokonano z dokładnością do 1/3 [°], tak więc do obliczeń przyjęto błąd
. Stałą siatki obserwowanego prążka wyznaczyliśmy ze wzoru:

gdzie l = 589.3 [nm] - średnia wartość długości fali żółtego dubletu sodu.

Wstawiając dane otrzymano trzy stałe siatki:

Błędy uzyskanych wartości obliczono z różniczki zupełnej:

Otrzymaliśmy trzy wartości stałej siatki wraz z błędami:

d₁ = (5422±174) nm

d₂ = (5188±37) nm

d₃ = (5134±146) nm

Ostateczną wartość stałej siatki obliczamy ze średniej ważonej, za pomocą programu komputerowego:

d = (51,9 ± 0,5)*10² nm

Pomiar długości fali światła laserowego

1. Siatkę dyfrakcyjną ustawiamy na stoliku, prostopadle do kierunku padania światła.

2. Notujemy położenia kolejnych jasnych prążków dyfrakcyjnych dla kilku (np. trzech) rzędów na lewo i prawo od prążka zerowego.

Ponieważ odczyt dokonujemy z dokładnością 1mm. więc tym samym przyjmujemy tę wartość jako błąd odczytu.

Tabelka pomiarowa:

Odległość siatki od ekranu l = (125 ± 0.5) cm

N	X [mm]
	Lewo	Prawo
1	160	170
2	348	347
3	548	555

3. Obliczamy długość światła laserowego korzystając ze wzoru:

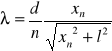
gdzie:

Do wzoru na długość światła laserowego za d podstawiamy stałą siatki dyfrakcyjnej obliczonej w poprzednim ćwiczeniu

d = 5.2 * 10^-6 m

Po obliczeniu otrzymano następujące wartości x_n:

Rząd prążka n	xn [m]
1	0.165
2	0.3475
3	0.551

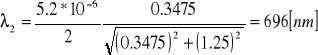
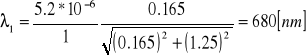
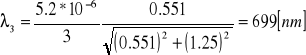
4. Przeprowadzamy rachunek błędów.

Błędy
obliczamy metodą różniczki zupełnej:

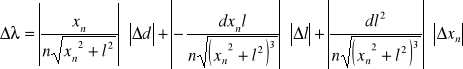
gdzie:

= 0.001 [m]

= 0.005 [m]

= 30 [nm]

Otrzymaliśmy następujące wartości:

= 4.0 [nm]

= 4.0 [nm]

= 3.9 [nm]

Za pomocą programu komputerowego obliczamy długość światła laserowego stosując metodę średniej ważonej:

= (692 ±4) [nm]

Wyznaczanie szerokości szczeliny

1. Szczelinę umieszczamy na stoliku na osi zestawu, prostopadle do kierunku światła laserowego.

2. Dobieramy szerokość szczeliny tak, aby na listwie pomiarowej uzyskać wyraźne prążki dyfrakcyjne z odstępem ok. 1 mm.

3. Suport powinien znajdować się w skrajnym położeniu. Aby uzyskać pełny obraz dyfrakcyjny, prążek centralny powinien być przesunięty w stosunku do szczeliny fotorezystora o ok. 10 do 12 mm.

4. Ustawiamy zakres miernika na 2 mA, ustalamy opcje programu i włączamy przesuw detektorze.

5. Za pomocą programu GRAPHER sporządzamy wykres widma energetycznego prążków dyfrakcyjnych.

6. Spisujemy z wykresu kolejne minima widma i obliczamy średnią odległość prążków od prążka zerowego tzn. średnie minima widma stosując wzór:

rząd minima n	położenie n-tego minima w lewo xnl [mm]		Położenie n-tego minima w prawo xnp [mm]	Średnia odległość minima od prążka zerowego xn [mm]
1		2,55	2.55	2,55
2		5,00	5,22	5,11
3		7,38	7,94	7,66

7. 
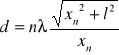
   Określamy położenie (i błędy położenia) kolejnych jasnych prążków :

gdzie:

n - numer kolejnego minimum (licząc od prążka centralnego),

l - odległość fotorezystora od badanej szczeliny,

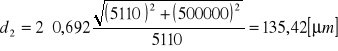
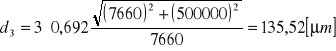
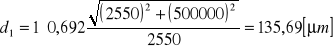
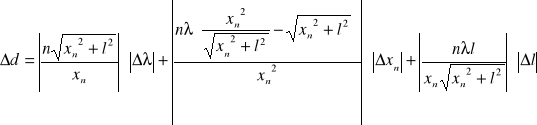
Błędy obliczamy metodą różniczki zupełnej:

gdzie:

l = 0.50 [m]

= 4 [nm]

= 0.001 [m]

= 0.005 [m]

Po wykonaniu obliczeń otrzymujemy:

= 5.6 [μm]

= 3.7 [μm]

= 2.8 [μm]

8. Obliczamy średnią wartość szerokości szczeliny korzystając z programu komputerowego na średnią ważoną:

d = (135.9 ±3.8) mm

WNIOSKI

Szerokość szczeliny wyznaczono za pomocą lasera, którego długość fali wynosi:

= (692 ±4) nm

oraz siatki dyfrakcyjnej, której stała wynosi:

d = (5190 ± 50) nm

Po podstawieniu do wzoru szerokość szczeliny wyniosła:

d = (135.5 ±3.5) μm

O błędzie wyznaczenia długości fali decyduje niepewność pomiarowa określenia położenia prążka dyfrakcyjnego. Wynika to z tego, że dla kolejnych rzędów obraz dyfrakcyjny powstały na ekranie jest coraz bardziej rozmazany i ciężko jest wyznaczyć dokładne położenie prążka dyfrakcyjnego. Należy także zaznaczyć, że ponieważ laser nie był przytwierdzony na stałe do stołu przypuszczalnie nie była zachowana prostopadłość wiązki lasera do tablicy pomiarowej co zapewne także wpłynęło na błąd obliczenia długości fali. Jednakże wartość uzyskanego wyniku jest poprawna, długość fali odpowiada kolorowi czerwonemu.

Pomiar szerokość szczeliny był wykonany bardzo precyzyjnie do czego przyczyniła się zapewne sama metoda pomiaru z zastosowaniem komputera.. Jednakże na wykresie zależności przesunięcia od natężenia prądu wyraźnie zauważamy różnicę w natężeniu prądu dla poszczególnych rzędów na prawo i lewo od centralnego prążka dyfrakcyjnego, co nie miało jednak wpływu na wyniki badań, ponieważ natężenie światła nie było brane podczas obliczeń pod uwagę.

EMBED AutoCAD.Drawing.14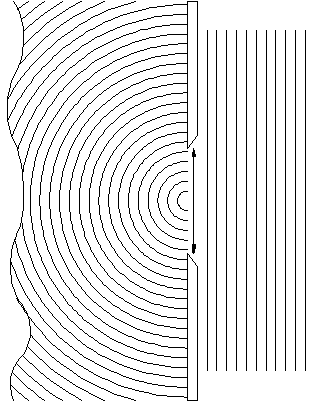

EMBED Equation.3

---