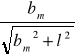Politechnika Śląska Wydział Inżynierii Materiałowej i Metalurgii
Fizyka Laboratorium
TEMAT: Wyznaczanie szerokości szczelin i stałych siatek dyfrakcyjnych na podstawie badania dyfrakcji promieniowania laserowego.
Uwagi prowadzącego:
Data przyjęcia: Podpis prowadzącego:		Imię i nazwisko: Monika Miękina Małgorzata Piękorz
				Grupa: ZIP20 Sekcja: VIII

OPIS PRZEBIEGU ĆWICZENIA

1. Wyznaczenie stałej siatki dyfrakcyjnej.

1. Umieszczenie siatki dyfrakcyjnej w uchwycie zamocowanym na ławie optycznej. Ustawienie uchwytu tak, aby w zakresie przemieszczeń fotoogniwa znalazły się prążki dyfrakcyjne od drugiego rzędu z lewej strony do drugiego rzędu z prawej strony.

2. Pomiar odległości siatki dyfrakcyjnej od fotoogniwa ustawionego w miejscu zerowego prążka dyfrakcyjnego.

3. Pomiar położenia prążków dyfrakcyjnych na podstawie obserwacji wartości sygnału napięciowego pochodzącego od fotoogniwa umieszczonego w centrum kolejnych prążków dyfrakcyjnych. Wykonanie pomiarów dla wszystkich prążków leżących w zakresie przemieszczeń fotoogniwa.

4. Powyższy pomiar wykonany dla trzech różnych odległości siatki dyfrakcyjnej od fotoogniwa.

OPRACOWANIE WYNIKÓW

A.Wyznaczanie stałej siatki dyfrakcyjnej.

1. Obliczanie wartości średniej (oraz odchylenia standardowego tej wartości) odległości badanej siatki od fotoogniwa.

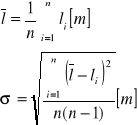
Podstawiając do wzorów wartości z pomiaru A.2 otrzymujemy wynik:

l = ( 178 ± 2 ) [10^-3m]

2. Obliczenie wartości średnich oraz odchyleń standardowych dla wyników pomiarów położenia prążka dyfrakcyjnego.

Wartość średnia x, cm	Odchylenie standardowe x, cm
-4) 24,67	0,15
-3) 21,58	0,06
-2) 18,87	0,06
-1) 16,47	0,06
0) 14,23	0,15
1) 12,1	0
2) 9,67	0,6
3) 7,1	0,1
4) 4,0	0,1

3. Obliczenie średnich odległości b_m lewego i prawego m-tego prążka dyfrakcyjnego od prążka zerowego. Obliczenie niepewności tych wyników.

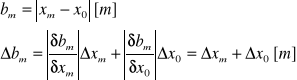
Wyniki obliczeń:

Nr prążka	bm, cm	Δ bm, %
4	10,36	0,11
3	7,24	0,16
2	4,45	0,25
1	2,19	0,50
0	0	0

4. Sporządzenie wykresu zależności
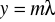
   od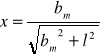
   .

λ = 0,623*10^-6 [m]

l = ( 178±2) [10^-3m]

Dane do wykresu:

m	bm [10^-3 m]	m·λ [10^-6m]
4	103,6	2,48	0,059
3	72,4	1,86	0,042
2	44,5	1,24	0,026
1	21,9	0,62	0,013
0	0	0	0

5. Wyznaczenie parametrów kierunkowych prostej aproksymującej zależność
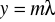
   od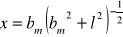
   .

Współczynniki kierunkowe prostej aproksymującej obliczamy zgodnie ze wzorami:

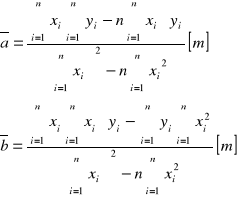
Niepewność wyznaczenia ww. współczynników obliczamy zgodnie ze wzorami:

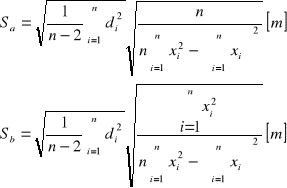
gdzie:

Prosta aproksymująca powyższą zależność ma następujące współczynniki kierunkowe:

a = ( 42,8± 1,8 ) [10^-6 m]

b = ( 0,07 ± 0,06 ) [10^-6 m]

6. Obliczenie odległość dwóch kolejnych szczelin w badanej siatce.

Porównując powyższy wzór z prostą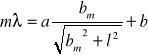
, otrzymujemy:

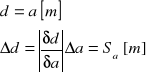
Wyliczona stała siatki dyfrakcyjnej wynosi:

d = ( 42,8 ± 1,8 ) [10^-6 m]

ZESTAWIENIE WYNIKÓW

1. Stała badanej siatki dyfrakcyjnej: d = (42,8± 1,8 )*[10^-6 m]

WNIOSKI

1. Precyzja pomiarów była uzależniona od dokładności sprzętu, który wykorzystaliśmy do ćwiczenia. Błędy odczytu wartości napięć wygenerowanych na fotoelemencie wynikały główne z powodu obecności zewnętrznego źródła oświetlenia w pobliżu elementu.

2. Obliczona stała siatki dyfrakcyjnej jest w przybliżeniu zgodna z wartością odczytaną z obudowy szczeliny, która wynosiła 6,7 · 10^-6 [m] (150 linii/mm).

3. Zależność iloczynu rzędu prążka i długość fali świetlnej od sinusa kąta ugięcia światła dla każdego zbadanego prążka dyfrakcyjnego jest liniowa.

4. Błędy w pomiarach są spowodowane niedokładnością odczytu wyników z przyrządów mierniczych.